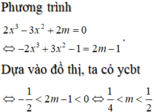y12x�12�b, −3x2
Đọc tiếp
b,
Những câu hỏi liên quan
khảo sát sự biến thiên và vẽ đồ thị hàm số:
a. y=x3-3x2+2
b. y=x3+1
9 tháng 3 2023 lúc 19:09
vẽ đồ thị hàm số:
Xem chi tiết
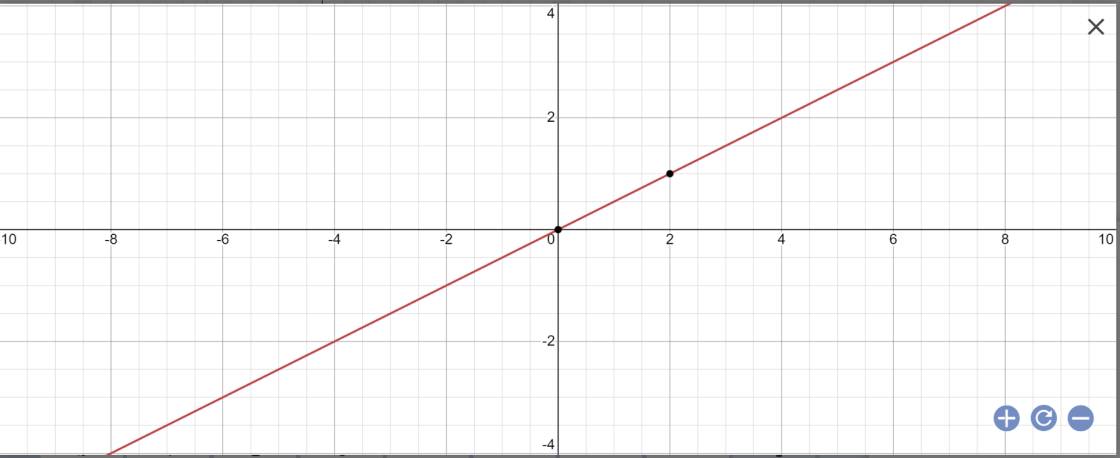
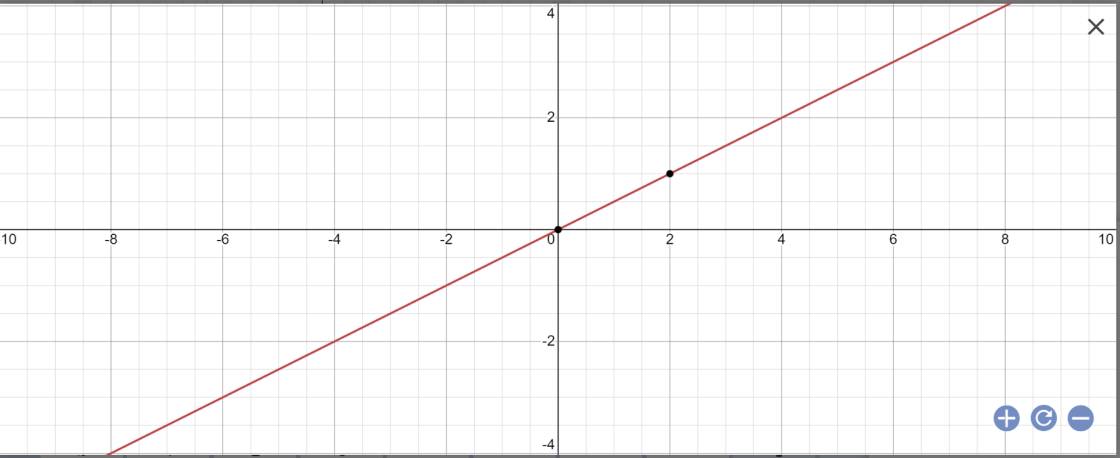
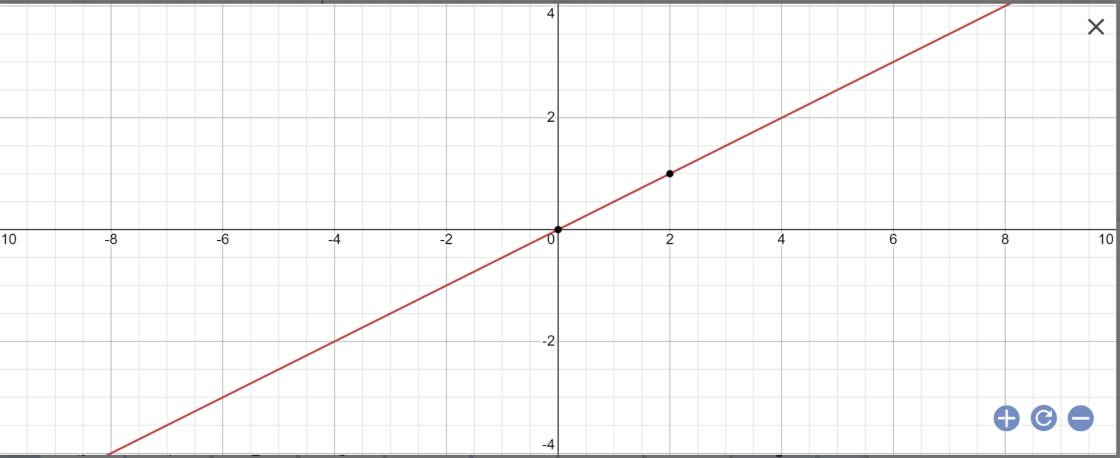
a, \(y=\dfrac{1}{2}x\)
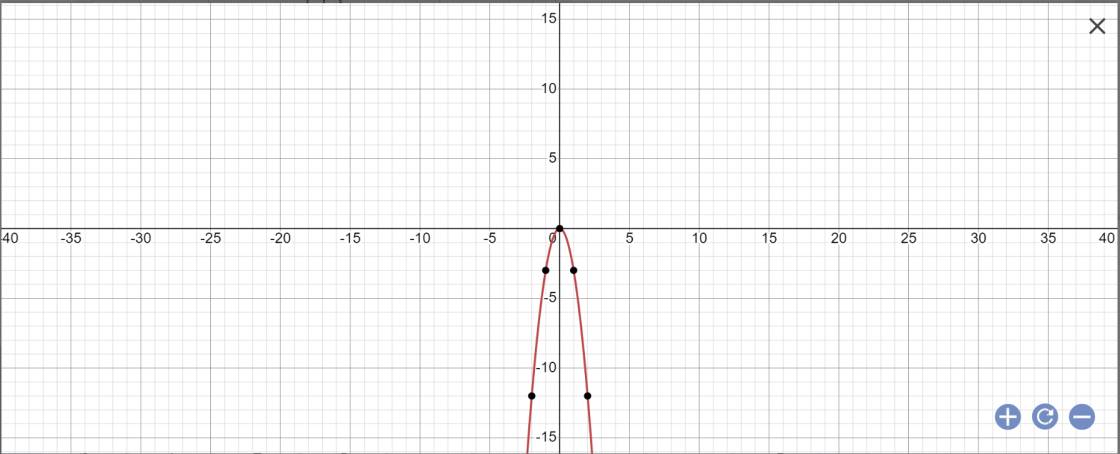
b, \(-3x^2\)
SGK Chân trời sáng tạo
20 tháng 8 2023 lúc 19:24
Vẽ đồ thị các hàm số:
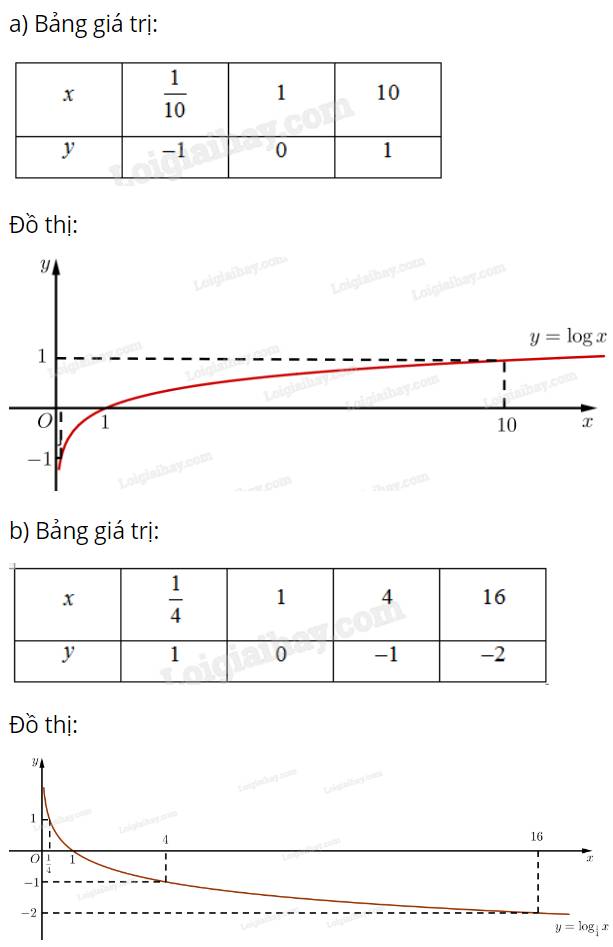
a) \(y = \log x\);
b) \(y = {\log _{\frac{1}{4}}}x\).
9 tháng 3 2023 lúc 19:37
vẽ đồ thị hàm số:a, y= 1/2xb, y= -3x^2
Xem chi tiết
9 tháng 3 2023 lúc 19:20
vẽ đồ thị hàm số:a, y= 1/2xb, y= -3x^2
Xem chi tiết
30 tháng 4 2021 lúc 16:00
B2:Vẽ đồ thị hàm số:
a)y=2x\(^2\)
b)y=\(\dfrac{-1}{2}x^2\)
c)y=2x+3
SGK Cánh Diều
13 tháng 8 2023 lúc 21:21
Lập bảng biến thiên và vẽ đồ thị hàm số:
a) \(y = {4^x}\)
b) \(y = {\log _{\frac{1}{4}}}x\)
a: Bảng biến thiên:
Đồ thị:
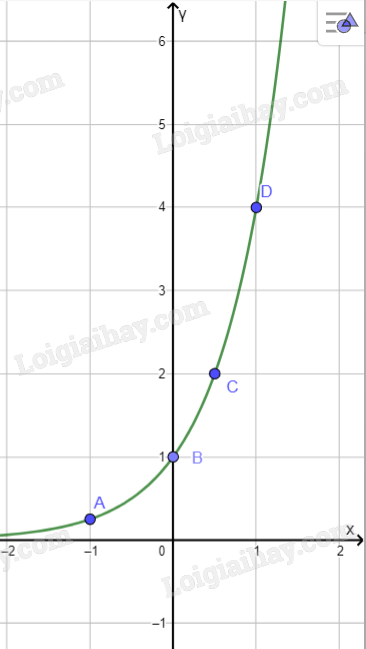
b: Bảng biến thiên:
Đồ thị: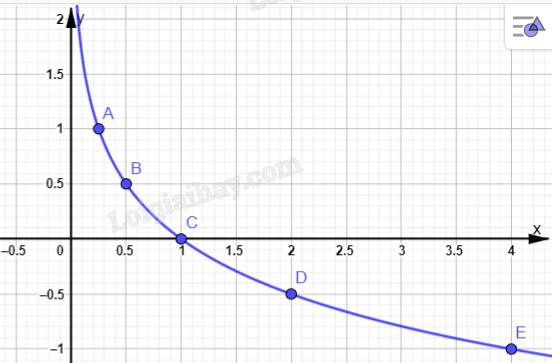 
Đúng 1
Bình luận (0)
Cho hàm số y 2x3 + 3x2 – 12x - 12. Gọi x1, x2 lần lượt là hoành độ hai điểm cực đại và cực tiểu của đồ thị hàm số. Kết luận nào sau đây là đúng? A. (x1 – x2)2 8 B. x1x2 2 C. x2 – x1 3 D. x12 + x22 6
Đọc tiếp
Cho hàm số y = 2x3 + 3x2 – 12x - 12. Gọi x1, x2 lần lượt là hoành độ hai điểm cực đại và cực tiểu của đồ thị hàm số. Kết luận nào sau đây là đúng?
A. (x1 – x2)2 = 8
B. x1x2 = 2
C. x2 – x1 = 3
D. x12 + x22 = 6
Đáp án C.
TXĐ: D = R.
Ta có y’ = 6x2 + 6x - 12, y’ = 0 ó 6x2 + 6x – 12 = 0 ó x = 1 hoặc x = -2.
y’’ = 12x + 12, y’’(1) = 24 > 0 => x2 = 1 là điểm cực tiểu, y’’(-2) = -12 < 0 => x1 - 2 là điểm cực đại.
Vậy ta có x2 – x1 = 3.
Đúng 0
Bình luận (0)
Cho hàm số
y
-
2
x
3
+
3
x
2
-
1
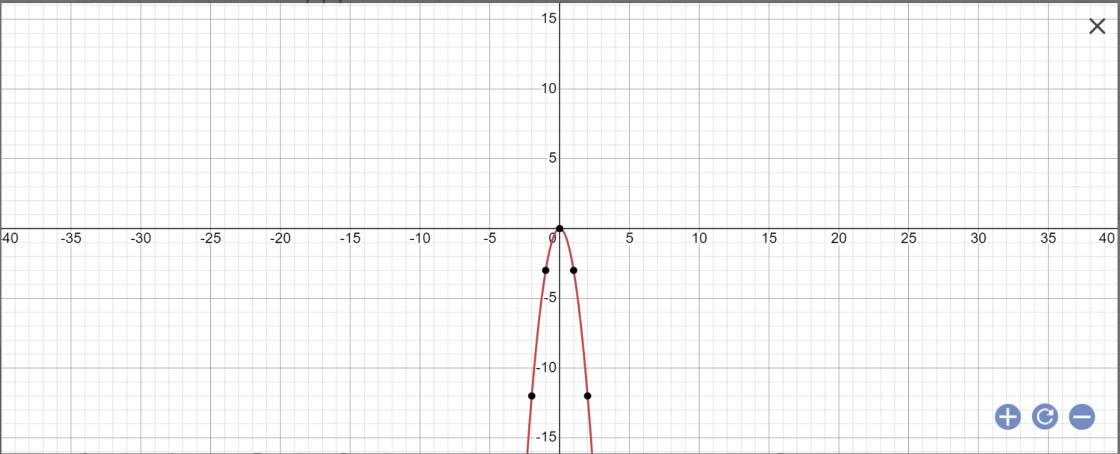
có đồ thị như hình vẽ. Bằng cách sử dụng đồ thị hàm số xác định m để phương trình
2
x
3
-
3
x
2
+
2
m
có đúng 3 nghiệm phân biệt, tron...
Đọc tiếp
Cho hàm số y = - 2 x 3 + 3 x 2 - 1 có đồ thị như hình vẽ. Bằng cách sử dụng đồ thị hàm số xác định m để phương trình 2 x 3 - 3 x 2 + 2 m có đúng 3 nghiệm phân biệt, trong đó có 2 nghiệm lớn hơn 1 2
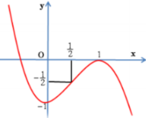
A. m ∈ - 1 2 ; 0
B. m ∈ - 1 ; 0
C. m ∈ 0 ; 1 2
D. m ∈ 1 4 ; 1 2
