cho tam giác abc có g là trọng tâm cm ga=gb=gc

Những câu hỏi liên quan
cho g là trọng tâm của tam giác abc abc là tam giác đều
cm ga =gb=gc
GA=GB=GC, G là trọng tâm tam giác kkhi và chỉ khi đso là tam giác đều.
Đề sai
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A có AB a; BC 2a và G là trọng tâm. Tính giá trị của biểu thức
G
A
→
.
G
B
→
+
G
B
→
.
G
C
→
+
G
C
→
....
Đọc tiếp
Cho tam giác ABC vuông tại A có AB = a; BC = 2a và G là trọng tâm.
Tính giá trị của biểu thức G A → . G B → + G B → . G C → + G C → . G A
A. -3a2
B. -2a2
C. -4 a2/3
D. 2a2
Chọn C.
Vì ![]() nên
nên
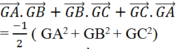
Gọi M, N, P lần lượt là trung điểm của BC, CA, AB
Tam giác ABM đều nên ![]()
Theo định lý Pitago ta có:
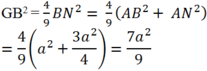
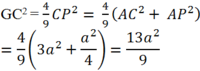
Suy ra
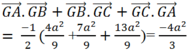
Đúng 0
Bình luận (0)
GIÚP EM VỚI Ạ, MAI EM THI RỒICâu 22: Cho tam giác ABC có trọng tâm G và trung tuyến AM. Khẳng định nào sau đây là sai:A. GA + GB + GC 0B. GA 2MGC. MB + CM CBD. GA + GB + CG 0
Đọc tiếp
GIÚP EM VỚI Ạ, MAI EM THI RỒI
Câu 22: Cho tam giác ABC có trọng tâm G và trung tuyến AM. Khẳng định nào sau đây là sai:
A. GA + GB + GC = 0
B. GA = 2MG
C. MB + CM = CB
D. GA + GB + CG = 0
cho G là trọng tâm của tam giác đều ABC cm rằng
GA=GB=GC
Cho tam giác ABC có AB = AC =5cm; BC =8cm. Gọi G là trọng tâm cụa tam giác .Tính GA, GB, GC
Gọi `AM` là trung tuyến của `ΔABC`
`=>AM` đồng thời là đường cao
`=>ΔAMB;ΔAMC⊥M`
`AM` là trung tuyến nên
`BM=MC=(BC)/2=4(cm)`
Áp dụng định lý py-ta-go ta tính được
`AM^2=AB^2-BM^2=5^2-4^2=25-16=9(cm)`
`=>AM=3cm`
`G` trọng tâm
`=>GA=2/3AM=2cm`
`GM=1/3AM=1cm`
Áp dụng định lý py-ta-go lần nữa ta tính đc
`GC^2=BG^2=BM^2+GM^2=4^2+1^2=16+1=17cm`
`=>GB=GC=`\(\sqrt{17cm}\)
Đúng 0
Bình luận (0)
cho tam giác abc có trọng tâm g trung điểm của ga gb gc lần lượt là m n p phép vị tâm g biến tam giác abc thành tam giác mnp có tỉ số là?
Cho tam giác ABC vuông tại A. Có AB=16cm, AC=30cm, G là trọng tâm của tam giác ABC. Tính GA+GB+GC?
cho G là trọng tâm tam giác đều ABC c/minh GA=GB=GC
Cho G là trọng tâm của tam giác đều ABC. Chứng minh rằng:
GA = GB = GC
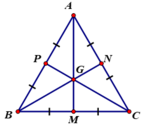
Gọi trung điểm BC, CA, AB lần lượt là M, N, P.
Khi đó AM, BN, CP đồng quy tại trọng tâm G.
Ta có: ∆ABC đều suy ra:
+ ∆ABC cân tại A ⇒ BN = CP (theo chứng minh bài 26).
+ ∆ABC cân tại B ⇒ AM = CP (theo chứng minh bài 26).
⇒ AM = BN = CP (1)
Vì G là trọng tâm của ∆ABC nên theo tính chất đường trung tuyến:
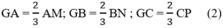
Từ (1) , (2) ⇒ GA = GB = GC.
Đúng 2
Bình luận (0)














