Mình đang cần gấp , ai trả lời được  mình sẽ tích nha

1,2,5,10,17,26,37,50,65

Đúng ko đó bạn 

Dãy số trên là dãy số cách đều với khoảng cách là:

93 109 - 93 009  = 100 

Vậy số tiếp theo cần điền vào chỗ còn thiếu là:

93 109 + 100 = 93 209

Đáp số: 93 209 

Dãy số trên là dãy số cách đều với khoảng cách là:

93 109 - 93 009  = 100 

Vậy số tiếp theo cần điền vào chỗ còn thiếu là:

93 109 + 100 = 93 209

Đáp số: 93 209 

Vì khoảng cách giữa hai số liền nhau là 100 nên số còn thiếu là 93 209

Câu trả lời là: 6;24;60;120;210 đó bạn!Chúc bạn học giỏi!

a. 7, 10, 13,16, 19, 22, 25.

b. 103, 95, 87,79, 71, 63, 55, 47.

A Qui luật các nhau 3 số 

16 , 19

79 , 31 , 63

16 , 19

79 , 31 , 63

mình nghĩ thế

bài 1 là 221

tôi nghĩ bài các bạn sẽ làm ngon ơ aingowf các bạn ko làm đc,tôi là một lập trình viên thật sự đấy

bài 1 là 221

bài 2 là 2129

\(\frac{1}{42}\) phải ko bạn

Ta thấy rằng:
\(\frac{1}{2}=\frac{1}{1.2}\)

\(\frac{1}{6}=\frac{1}{2.3}\)

\(\frac{1}{12}=\frac{1}{3.4}\)

\(\frac{1}{20}=\frac{1}{4.5}\)

\(\frac{1}{30}=\frac{1}{5.6}\)

Vậy số hạng cần tìm = \(\frac{1}{6.7}=\frac{1}{42}\)

       Đáp số: \(\frac{1}{42}\)

1/42 đó bạn

thiếu dãy số rùi bn ơi

a) \(n = 100 \Leftrightarrow \left| {{u_{100}}} \right| = \left| {\frac{{{{\left( { - 1} \right)}^{100}}}}{{100}}} \right| = \frac{1}{{100}} = 0,01\)

\(n = 1000 \Leftrightarrow \left| {{u_{1000}}} \right| = \left| {\frac{{{{\left( { - 1} \right)}^{1000}}}}{{1000}}} \right| = \frac{1}{{1000}} = 0,001\)

Như vậy ta có thể điền vào bảng như sau:

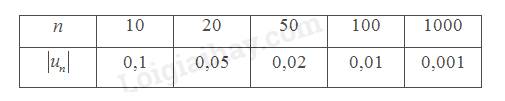
b) \(\left| {{u_n}} \right| < 0,01 \Leftrightarrow \left| {\frac{{{{\left( { - 1} \right)}^n}}}{n}} \right| < 0,01 \Leftrightarrow \frac{1}{n} < 0,01 \Leftrightarrow n > 100\)

Vậy \(\left| {{u_n}} \right| < 0,01\) khi \(n > 100\).

\(\left| {{u_n}} \right| < 0,001 \Leftrightarrow \left| {\frac{{{{\left( { - 1} \right)}^n}}}{n}} \right| < 0,001 \Leftrightarrow \frac{1}{n} < 0,001 \Leftrightarrow n > 1000\)

Vậy \(\left| {{u_n}} \right| < 0,001\) khi \(n > 1000\).

c) Dựa vào trục số ta thấy, khoảng cách từ điểm \({u_n}\) đến điểm 0 trở nên rất bé khi \(n\) trở nên rất lớn.