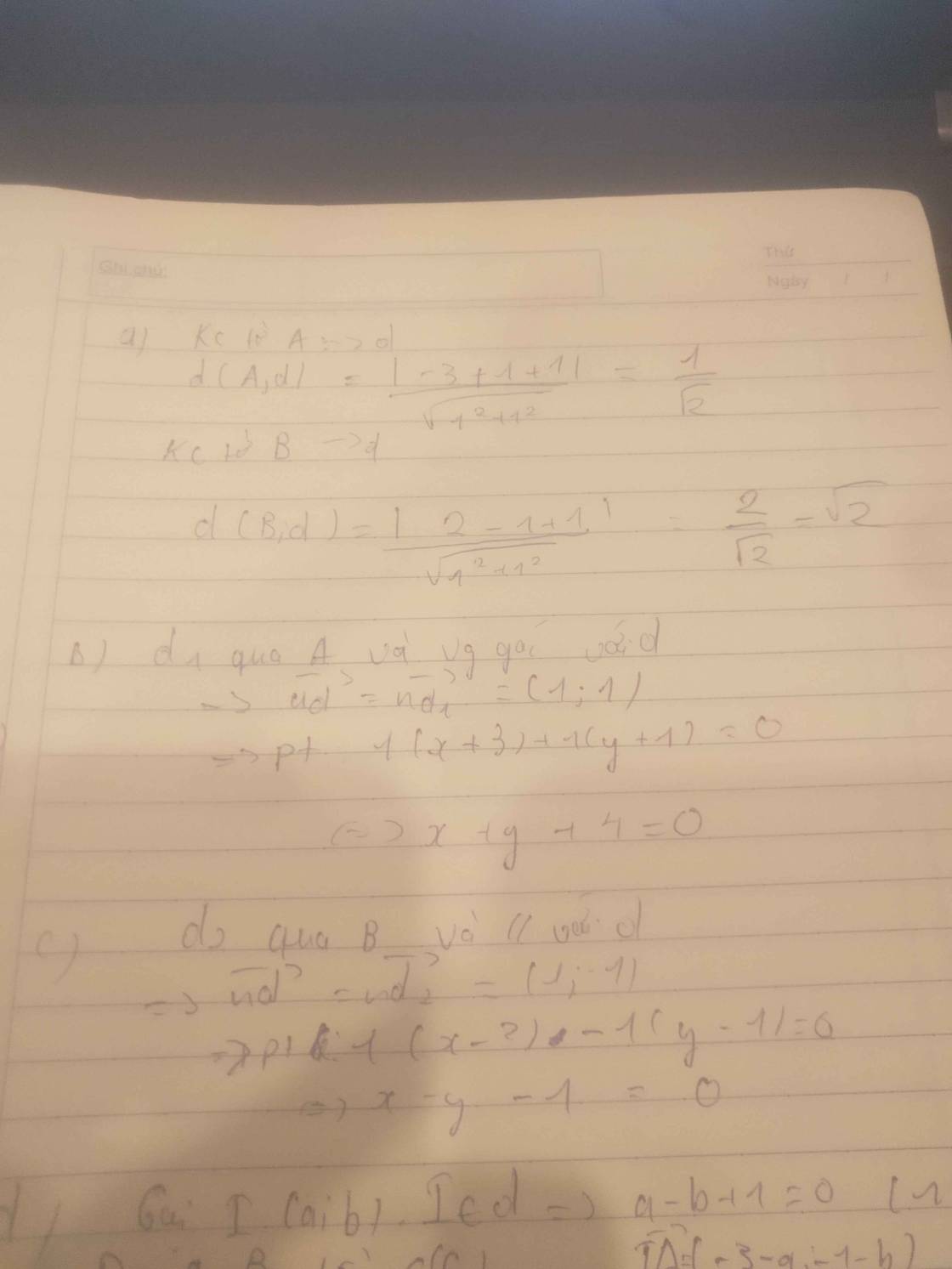Cho đường thẳng \(\Delta:x+y-1=0\) . Viết phương trình đường thẳng d đi qua A(1;1) và tạo với đường thẳng \(\Delta\) một góc \(45^o\) .

Những câu hỏi liên quan
Cho đường thẳng \(\Delta:x+y-1=0\), viết phương trình d đi qua A(1;1) và tạo với \(\Delta\) một góc 60 độ.
Ta có đường thẳng \(\Delta\) có hệ số góc \(k=-1\) do đó góc giữa \(\Delta\) và Ox bằng \(45^0\). Do d tạo với \(\Delta\) góc \(60^0\) nên d không có phương vuông góc với Ox. Gọi l là hệ số góc của d khi đó d có phương trình : \(y=l\left(x-1\right)+1\).
Theo định lí ta có :
\(\left|\frac{k-l}{1+kl}\right|=\tan60^0\)\(\Leftrightarrow\left|l+1\right|=\sqrt{3}.\left|1-l\right|\)
Giải phương trình ta được \(l=2\pm\sqrt{3}\)
Vậy ta tìm được 2 đường thẳng thỏa mãn \(d:y=\left(2\pm\sqrt{3}\right)\left(x-1\right)+1\)
Đúng 0
Bình luận (0)
Bài 1: Cho đường thẳng d:left{begin{matrix}x1+ty-1+2tend{matrix}right.. Viết phương trình đường thẳng d dưới dạng chính tắc và tổng quát.
Bài 2: Cho đường thẳng d:frac{x-2}{-1}frac{y+1}{2}. Viết phương trình tổng quát và tham số của d.
Bài 3: Viết phương trình đường thẳng d trong các trường hợp:
a, Đi qua Mleft(1;2right) và song song với đường thẳng Delta:x+2y-10
b, Đi qua Mleft(1;2right) và vuông góc với đường thẳng Delta:x+2y-10
Đọc tiếp
Bài 1: Cho đường thẳng \(d:\left\{\begin{matrix}x=1+t\\y=-1+2t\end{matrix}\right.\). Viết phương trình đường thẳng \(d\) dưới dạng chính tắc và tổng quát.
Bài 2: Cho đường thẳng \(d:\frac{x-2}{-1}=\frac{y+1}{2}\). Viết phương trình tổng quát và tham số của \(d\).
Bài 3: Viết phương trình đường thẳng \(d\) trong các trường hợp:
a, Đi qua \(M\left(1;2\right)\) và song song với đường thẳng \(\Delta:x+2y-1=0\)
b, Đi qua \(M\left(1;2\right)\) và vuông góc với đường thẳng \(\Delta:x+2y-1=0\)
1. Ta có: \(d\) đi qua điểm \(M\left(1;-1\right)\) và có vec-tơ chỉ phương \(\overrightarrow{u}\left(1;2\right)\). Suy ra \(d\) có 1 vec-tơ pháp tuyến \(\overrightarrow{n}\left(2;-1\right)\).
Phương trình chính tắc của \(d:\frac{x-1}{1}=\frac{y+1}{2}\)
Phương trình tổng quát của \(d:2\left(x-1\right)-1\left(y+1\right)=0\Leftrightarrow2x-y-3=0\)
Đúng 0
Bình luận (3)
2. Ta có: \(d\) đi qua \(M\left(2;-1\right)\) và nhận vec-tơ \(\overrightarrow{u}\left(-1;2\right)\) làm vec-tơ chỉ phương. Suy ra \(d\) có 1 vec-tơ pháp tuyến \(\overrightarrow{n}\left(2;1\right)\)
Phương trình tham số chủa đường thẳng \(d:\left\{\begin{matrix}x=2-t\\y=-1+2t\end{matrix}\right.\)
Phương trình tổng quát của \(d:2\left(x-2\right)+1\left(y+1\right)=0\Leftrightarrow2x+y-3=0\)
Đúng 0
Bình luận (1)
Trong mặt phẳng Oxy cho ba điểm A(-6;3), B(0;-1), C(3;2) a) Viết phương trình tham số với đường thẳng AB b) Viết phương trình đường thẳng d đi qua C và vuông góc với đường thẳng AB c) Tìm tọa độ điểm m trên đường thẳng d 2x- y + 3 = 0 sao cho | vectơ MA + vectơ MB + MC| nhỏ nhất
Trong mặt phẳng Oxy cho ba điểm A(-6;3), B(0;-1), C(3;2) a) Viết phương trình tham số với đường thẳng AB b) Viết phương trình đường thẳng d đi qua C và vuông góc với đường thẳng AB c) Tìm tọa độ điểm m trên đường thẳng d 2x- y + 3 = 0 sao cho | vectơ MA + vectơ MB + MC| nhỏ nhất
a: vecto AB=(6;-4)
PTTS là:
x=-6+6t và y=3-4t
b: Vì (d) vuông góc AB nên (d) có VTPT là (3;-2)
Phương trình(d) là:
3(x-3)+(-2)(y-2)=0
=>3x-9-2y+4=0
=>3x-2y-5=0
Đúng 0
Bình luận (0)
Trong mặt phẳng Oxy cho A (4;1), B (-2;3), C (5;-1). a) Viết phương trình tham số và trình tổng quát của đường thẳng đi qua hai điểm A,C b) Viết phương trình tham số và trình tổng quát của đường thẳng A và vuông góc với B,C c) Viết phương trình tham số và trình tổng quát của đường thẳng qua A và song song với đường thẳng d : 2x - y + 3 = 0
Trong mặt phẳng toạ độ Oxy, cho hai điểm A(3;1),B(4;-2) và đường thẳng d: -x+2y+1=0. a) Viết phương trình tham số của Δ đi qua A song song với đường thẳng d b) Viết phương trình tổng quát của Δ đi qua B và vuông góc với đường thẳng d c) Viết phương trình đường tròn có bán kính AB
a: (Δ)//d nên Δ: -x+2y+c=0
=>VTPT là (-1;2)
=>VTCP là (2;1)
PTTS là:
x=3+2t và y=1+t
b: (d): -x+2y+1=0
=>Δ: 2x+y+c=0
Thay x=4 và y=-2 vào Δ, ta được:
c+8-2=0
=>c=-6
Đúng 0
Bình luận (0)
Cho điểm A(-3;-1), B(2;1), đường thẳng d: x-y+1=0.
a. Tính khoảng cách từ A, B đến đường thẳng d.
b. Viết pt đường thẳng d1 đi qua A và vuông góc với d.
c. Viết phương trình đthẳng d2 đi qua B và song song với d.
d. Viết pt đường tròn (C) có tâm I thuộc d và đi qua 2 điểm A, B
Cho đường thẳng d:
x
1
+
t
y
2
t
z
-
1
và mặt phẳng (P): 2x+y-2z-10. Viết phương t...
Đọc tiếp
Cho đường thẳng d: x = 1 + t y = 2 t z = - 1 và mặt phẳng (P): 2x+y-2z-1=0. Viết phương trình đường thẳng đi qua M(1;2;1), song song với (P) và vuông góc với đường thẳng d.
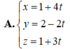
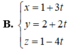
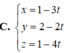
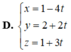
. Cho điểm A(1; 2) và đường thẳng d: 2x - 3y - 1 = 0 Viết phương trình đường thẳng delta đi qua A và vuông góc với d.
Lời giải:
VTPT của $(d)$: $(2,-3)$
Đường thẳng $\Delta$ vuông góc với $(d)$ nên VTCP của $(\Delta)$ chính là $(2,-3)$
$\Rightarrow$ VTPT $ của $(\Delta)$ là $(3,2)$
PTĐT $(\Delta)$: $3(x-1)+2(y-2)=0$
$\Leftrightarrow 3x+2y-7=0$
Đúng 1
Bình luận (0)