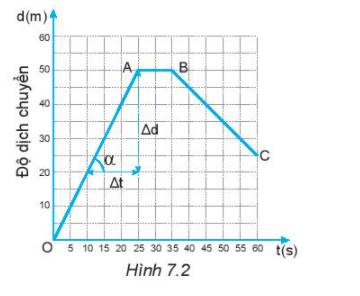
Hãy xác định vận tốc và tốc độ của người bơi từ giây 45 đến giây 60 bằng đồ thị ở Hình 7.2.
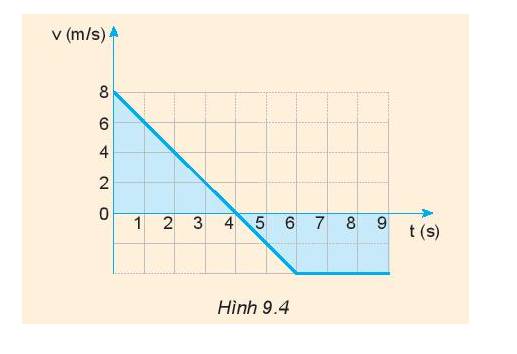
Hãy dùng đồ thị (v – t) vẽ ở hình 9.4 để:
a) Mô tả chuyển động
b) Tính độ dịch chuyển trong 4 giây đầu, 2 giây tiếp theo và 3 giây cuối
c) Tính gia tốc của chuyển động trong 4 giây đầu
d) Tính gia tốc của chuyển động từ giây thứ 4 đến giây thứ 6.
Kiểm tra kết quả của câu b và câu c bằng cách dùng công thức.
a) Mô tả chuyển động:
- Trong 4 giây đầu tiên: chuyển động chậm dần đều từ 8 m/s đến 0 m/s
- Từ giây thứ 4 đến giây thứ 6: bắt đầu tăng tốc với vận tốc -2 m/s
- Từ giây thứ 6 đến giây thứ 9: chuyển động thẳng đều với vận tốc – 2 m/s
b) Độ dịch chuyển:
- Trong 4 giây đầu:
Độ dịch chuyển bằng diện tích tam giác vuông có cạnh đáy là t và chiều cao là v.
\({d_1} = \frac{1}{2}.{t_1}.{v_1} = \frac{1}{2}.4.8 = 16\left( m \right)\)
- Trong 2 giây tiếp theo:
Độ dịch chuyển bằng diện tích tam giác vuông có cạnh đáy là t và chiều cao là v.
\({d_2} = \frac{1}{2}.{t_2}.{v_2} = \frac{1}{2}.2.( - 4) = - 4\left( m \right)\)
- Trong 3 giây cuối:
Độ dịch cuyển bằng diện tích hình chữ nhật có chiều dài là t và chiều rộng là v.
\({d_3} = {v_3}.{t_3} = - 4.3 = - 12\left( m \right)\)
c)
Gia tốc của chuyển động trong 4 giây đầu:
\(a = \frac{{\Delta v}}{{\Delta t}} = \frac{{0 - 8}}{{4 - 0}} = - 2\left( {m/{s^2}} \right)\)
d)
Gia tốc của chuyển động từ giây thứ 4 đến giây thứ 6:
\(a = \frac{{\Delta v}}{{\Delta t}} = \frac{{ - 4 - 0}}{{6 - 4}} = - 2\left( {m/{s^2}} \right)\)
* Kiểm tra kết quả bằng công thức:
Độ dịch chuyển:
- Trong 4 giây đầu:
\({d_1} = {v_0}.{t_1} + \frac{1}{2}.a.t_1^2 = 8.4 + \frac{1}{2}.( - 2){.4^2} = 16(m)\)
- Trong 2 giây tiếp theo:
\({d_2} = {v_0}{t_2} + \frac{1}{2}a{t_2}^2 = 0.2 + \frac{1}{2}.( - 2){.2^2} = - 4\left( m \right)\)
- Trong 3 giây cuối:
\({d_3} = {v_3}t = - 4.3 = - 12\left( m \right)\)
=> Trùng với kết quả khi dùng đồ thị.
Câu 1: Trên hình bên là đồ thị độ dịch chuyển - thời gian của một vật chuyển động trên một đường thẳng. Hãy cho biết:
- Tốc độ và vận tốc của vật trong mỗi giai đoạn.
- Độ dịch chuyển và quãng đường vật đi được trong 4 giây đầu tiên, giây thứ 4 đến giây thứ 12, giây thứ 12 đến giây thứ 16, 12 giây đầu và trên cả đoạn đường
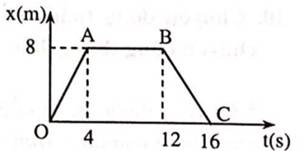
Từ O-A: Vận tốc của vật là: \(v=\dfrac{s}{t}=\dfrac{8}{4}=2\left(\dfrac{m}{s}\right)\)
Độ dịch chuyển trong 4 giây đầu: d=8(m)
Quãng đường vật đi được trong 4 giây đầu: s=8(m)
Từ A-B: Vận tốc của vật là: v=0 (m/s)
Độ dịch chuyển trong giây thứ 4 đến giây thứ 12: d=0(m)
Quãng đường vật đi được trong giây thứ 4 đến giấy thứ 12: s=0(m)
Từ B-C: Vận tốc của vật là: \(v=\dfrac{s}{t}=\dfrac{8}{16-12}=2\left(\dfrac{m}{s}\right)\)
Độ dịch chuyển trong giây 12 đến giây thứ 16 là: d=8(m)
Quãng đường vật đi được trong giây thứ 12 đến giây thứ 16: s=8(m)
Độ dịch chuyển trong 12 giây đầu: 8(m)
Quãng đường đi được trong 12 giây đầu: 8(m)
Độ dịch chuyển trên cả đoạn đường: d=0 (m)
Quãng đường đi được trên cả đoạn đường: 16(m)
Hình 7.2 là đồ thị độ dịch chuyển – thời gian của một người đang bơi trong một bể bơi dài 50 m. Đồ thị này cho biết những gì về chuyển động của người đó?

1. Trong 25 giây đầu mỗi giây người đó bơi được bao nhiêu mét? Tính vận tốc của người đó ra m/s
2. Từ giây nào đến giây nào người đó không bơi?
3. Từ giây 35 đến giây 60 người đó bơi theo chiều nào?
4. Trong 20 giây cuối cùng, mỗi giây người đó bơi được bao nhiêu mét? Tính vận tốc của người đó ra m/s.
5. Xác định độ dịch chuyển và vận tốc của người đó khi bơi từ B đến C.
6. Xác định độ dịch chuyển và vận tốc của người đó trong cả quá trình bơi.
1.
Từ đồ thị ta thấy, trong 25s đầu người đó chuyển động thẳng từ O – A và không đổi chiều, độ dịch chuyển trong 25 s đầu là 50 m.
Suy ra: Mỗi giây người đó bơi được: \(\frac{{50}}{{25}} = 2\left( m \right)\)
Vận tốc của người đó là: \(v = \frac{d}{t} = \frac{{50}}{{25}} = 2\left( {m/s} \right)\)
2.
Từ A – B: người đó không bơi => Người đó không bơi từ giây 25 đến giây 35.
3.
Từ giây 35 đến giây 60 người đó bơi ngược chiều dương.
Một ô tô bắt đầu chuyển động với vận tốc v t = a t 2 + b t với t tính bằng giây và v tính bằng mét/giây, sau 10 giây thì đạt vận tốc cao nhất v =50 và giữ nguyên vận tốc đó, có đồ thị vận tốc như hình sau.

Tính quãng đường s ô tô đi được trong 20 giây ban đầu.
A. s = 800
B. s = 2000/3
C. s = 2500/3
D. s =2600/3
Cho đồ thị độ dịch chuyển - thời gian của một người đang bơi trong một bể bơi dài 50m.

a) Tính tốc độ chuyển động trong 25s đầu
b) Từ t = 35s đến t = 60s người đó bơi theo chiều nào với tốc độ bao nhiêu?
c) Xác định độ dịch chuyển trong cả quá trình bơi
a) Để tính tốc độ chuyển động trong 25s đầu, chúng ta cần biết độ dịch chuyển trong khoảng thời gian đó. Từ đồ thị, chúng ta có thể thấy rằng độ dịch chuyển trong 25s đầu là khoảng 40m. Vì vậy, tốc độ chuyển động trong 25s đầu là:
tốc độ = độ dịch chuyển / thời gian = 40m / 25s = 1.6 m/s
b) Để xác định chiều và tốc độ chuyển động từ t = 35s đến t = 60s, chúng ta cần xem xét đường cong đồ thị trong khoảng thời gian này. Nếu đường cong đồ thị nằm trên trục dương, người đó đang bơi về phía dương, và nếu nằm trên trục âm, người đó đang bơi về phía âm.
Trong trường hợp này, chúng ta không có thông tin cụ thể về đồ thị. Vì vậy, không thể xác định được chiều di chuyển.
c) Để tính độ dịch chuyển trong cả quá trình bơi, chúng ta cần tính tổng diện tích dưới đường cong đồ thị trong khoảng thời gian từ t = 0s đến t = 60s. Khi đó, diện tích dưới đường cong đồ thị sẽ tương đương với độ dịch chuyển.
Tuy nhiên, vì chúng ta không có đồ thị cụ thể, không thể tính được độ dịch chuyển trong cả quá trình bơi.
\(a,\) Gọi điểm tại \(t=25s\) là H.
Tốc độ chuyển động trong 25s đầu là :
\(v_A=\left|+\dfrac{AH}{OH}\right|=\left|\dfrac{50}{25}\right|=2m/s\)
\(b,t=35s\rightarrow t=60s\) : người đó bơi theo chiều âm \(\left(-\right)\) (Do đường thẳng trên đồ thị đi xuống).
\(v=\left|\dfrac{d}{\Delta t}\right|=\left|-\dfrac{50}{60-35}\right|=\left|-2\right|=2m/s\)
\(c,\) Quá trình bơi được chia thành 3 lần khác nhau theo đồ thị biểu diễn :
+ Lần 1 : Từ \(0s\rightarrow25s\) : theo chiều dương \(\left(+\right)\) nên ta có tốc độ dịch chuyển lúc này chính là \(v_A=2m/s\)
+ Lần 2: Từ \(25s\rightarrow35s\) : người đó đứng yên nên tốc độ dịch chuyển lúc này \(=0\).
+ Lần 3 : Từ \(35s\rightarrow60s\) : theo chiều âm \(\left(-\right)\) nên ta có tốc độ dịch chuyển lúc này chính là \(v=2m/s\)
Vậy tốc độ dịch chuyển trong cả quá trình bơi là : \(2+0+2=4m/s\).
Một vật được thả theo phương thẳng đứng từ độ cao 20m xuống đất với vận tốc tại thời điểm bắt đầu là 5m/s. Vật chuyển động thẳng nhanh dần đều, cứ sau mỗi giây, vận tốc rơi tăng thêm 10m/s.
Giả sử vận tốc của vật được xác định theo hàm số y=ax+b với y được tính bằng m/s, x được tính bằng số giây kể từ khi vật được thả.
Biết thời gian của vật bị thả đến lúc chạm đất là 2 giây và vận tốc của vật lúc chạm đất là 25m/s.
Xác định a,b
đề bài hơi rắc rối, giúp mình nhé!
123 dô 23 dô 34 uống
câu hỏi dài thế làm anh đau đầu quá em ạ
Đồ thị toạ độ - thời gian của vật chuyển động thẳng mô tả ở hình bên. Tỉ lệ về tốc độ của vật trong giây đầu và hai giây sau là
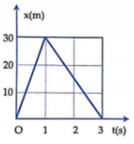
A. 1 : 2
B. 1 : 3
C. 3 : 1
D.2 : 1
Đáp án D
Tốc độ của vật trong giây đầu là: 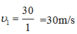
Tốc độ của vật trong hai giây sau là: 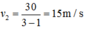
Vậy tỉ lệ về tốc độ trong giây đầu và hai giây sau là 2 : 1