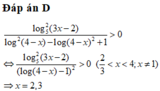-Tham khảo:

https://hoc24.vn/hoi-dap/tim-kiem?id=45441263315&q=T%C3%ACm%20nghi%E1%BB%87m%20nguy%C3%AAn%20c%E1%BB%A7a%20ph%C6%B0%C6%A1ng%20tr%C3%ACnh%20sau%C2%A0%5C%28x%5E6%203x%5E2%201%3Dy%5E4%5C%29

Ta có:

\(x^6+3x^2+1=y^4\)

\(\Leftrightarrow4x^6+12x^3+4=4y^4\)

\(\Leftrightarrow4x^6+12x^3+9=4y^4+5\)

\(\Leftrightarrow\left(2x^3+3\right)^2-4y^4=5\)

\(\Leftrightarrow\left(2x^3+2y^2+3\right)\left(2x^3-2y^2+3\right)=5\)

\(\Rightarrow\orbr{\begin{cases}2x^3+2y^2+3=5\\2x^3-2y^2+3=1\end{cases}}\)\(\Leftrightarrow\orbr{\begin{cases}x=0;y=1\\x=0;y=-1\end{cases}}\)

\(\Rightarrow\orbr{\begin{cases}2x^3+2y^2+3=-1\\2x^3-2y^2+3=-5\end{cases}\Leftrightarrow x=\sqrt[3]{-6}}\) (loại)

Vậy PT có nghiệm \(\left(x;y\right)=\left(0;1\right);\left(0;-1\right)\)

Em mới học lớp 5 à

Có x6+3x2+1=y3>x6x6+3x2+1=y3>x6 (1)(1)

x6+3x2+1=y3\leqx6+3x4+3x2+1=(x2+1)3(2)x6+3x2+1=y3\leqx6+3x4+3x2+1=(x2+1)3(2)

(1);(2)(1);(2) suy ra x6+3x2+1=(x2+1)3x6+3x2+1=(x2+1)3 suy ra x=0;y=1

Đây là đáp án đúng nhất :

Ta có :
(x2+1)3=x6+3x4+3x2+1≥x6+3x2+1>(x3)2(x2+1)3=x6+3x4+3x2+1≥x6+3x2+1>(x3)2
Mà : x6+3x2+1=y3x6+3x2+1=y3
⇒x6+3x2+1=(x2+1)3⇒x=0⇒y=1⇒x6+3x2+1=(x2+1)3⇒x=0⇒y=1

a/ \(x^3-3x^2+3x-2=0\)

\(\Leftrightarrow x^3-2x^2-x^2+2x+x-2=0\)

\(\Leftrightarrow x^2\left(x-2\right)-x\left(x-2\right)+\left(x-2\right)=0\)

\(\Leftrightarrow\left(x-2\right)\left(x^2-x+1\right)=0\)

\(\Leftrightarrow\orbr{\begin{cases}x-2=0\\x^2-x+1=0\end{cases}}\)

\(\Leftrightarrow\orbr{\begin{cases}x=2\left(tm\right)\\\left(x-\frac{1}{2}\right)^2+\frac{3}{4}=0\left(ktm\right)\end{cases}}\)

Vậy x = 2 là nghiệm của phương trình.

b/ \(\left(x+y\right)^2=\left(x-1\right)\left(y+1\right)\)

\(\Leftrightarrow2\left(x+y\right)^2=2\left(x-1\right)\left(y+1\right)\)

\(\Leftrightarrow2x^2+4xy+2y^2=2xy+2x-2y-2\)

\(\Leftrightarrow2x^2+2y^2+2xy-2x+2y+2=0\)

\(\Leftrightarrow\left(x^2-2x+1\right)+\left(y^2+2y+1\right)+\left(x^2+2xy+y^2\right)=0\)

\(\Leftrightarrow\left(x-1\right)^2+\left(y+1\right)^2+\left(x+y\right)^2=0\)

Mà \(\left(x-1\right)^2\ge0\)

      \(\left(y+1\right)^2\ge0\)

      \(\left(x+y\right)^2\ge0\)

Dấu " = " xảy ra \(\Leftrightarrow\hept{\begin{cases}x=1\\y=-1\end{cases}}\)

Vậy \(x=1;y=-1\Leftrightarrow\left(x+y\right)^2=\left(x-1\right)\left(y+1\right)\)