Giúp mình mấy bài này với. Mình xin cảm ơn!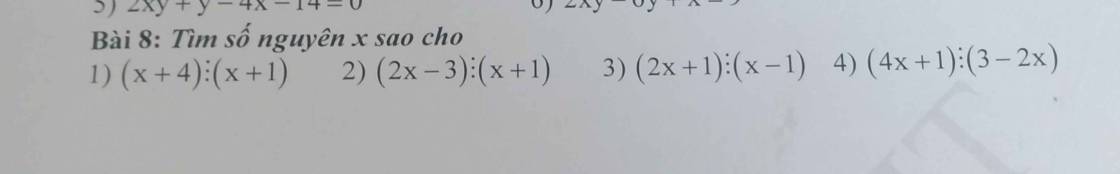

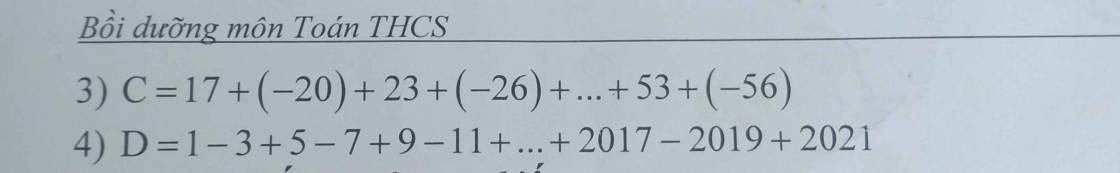
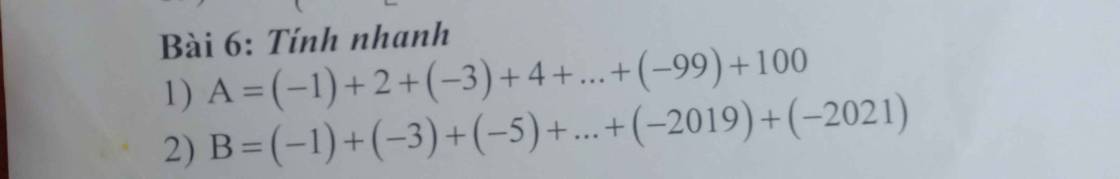
Giúp mình bài này với. Mình cần gấp lắm !!! Xin cảm ơn!

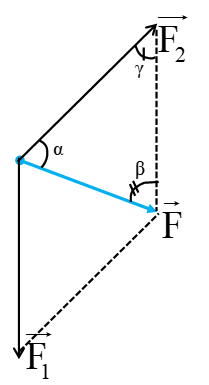
Theo định lí \(sin\):
\(\dfrac{sin\alpha}{F_1}=\dfrac{sin\beta}{F_2}=\dfrac{sin\gamma}{F}\)\(\Rightarrow F_2=\dfrac{F_1}{sin\alpha}\cdot sin\beta\)
\(F_{min}\Leftrightarrow sin\alpha=1\Rightarrow\alpha=90^o\)
\(\Rightarrow\beta=120-90=60^o\)
\(\Rightarrow F_2=\dfrac{6}{1}\cdot sin60^o=3\sqrt{3}N\)
Giúp mình bài này với. Mình cần gấp lắm !!! Xin cảm ơn!

Coi điểm tựa G là trung điểm AB.
Ta có hệ:
\(\left\{{}\begin{matrix}AH+HB=L=80\\3AH=HB\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}AH=20\\BH=60\end{matrix}\right.\)
\(\Rightarrow HG=\dfrac{1}{4}AB=\dfrac{1}{4}\cdot80=20cm\)
\(\Rightarrow GB=BH-HG=60-20=40cm\)
Giúp mình bài này với. Mình cần gấp lắm !!! Xin cảm ơn!

Giúp mình bài này với. Mình cần gấp lắm !!! Xin cảm ơn!

Giúp mình bài này với ạ, mình cần gấp lắm. Xin cảm ơn

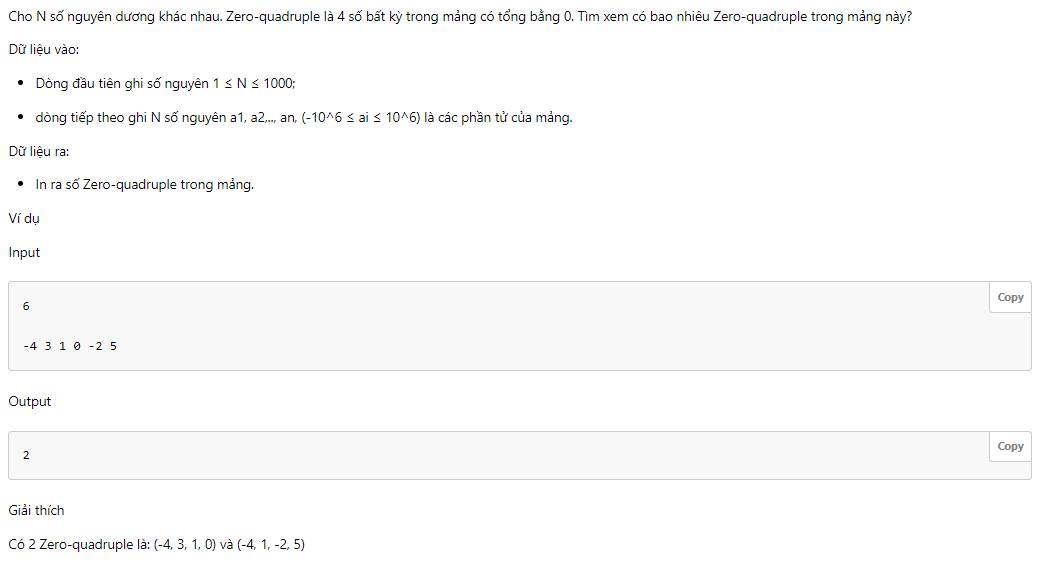 Bạn nào biết làm bài này ko làm giúp mình với mình đang cần bài này ạ! Xin cảm ơn
Bạn nào biết làm bài này ko làm giúp mình với mình đang cần bài này ạ! Xin cảm ơn
Bạn tham khảo code C++ nhé
Giúp mình bài này với ạ. Mình cần gấp lắm ạ. Xin cảm ơn!!

 ai giúp mình hai bài này với ạ, mình cần gấp xin cảm ơn
ai giúp mình hai bài này với ạ, mình cần gấp xin cảm ơn
Bài 4:
a: Xét ΔBFC có
FP,BA là các đường cao
FP cắt BA tại E
Do đó: E là trực tâm của ΔBFC
=>CE⊥BF tại Q
b: AMPN là hình vuông
=>AP là phân giác của góc MAN
=>\(\hat{MAP}=\hat{NAP}=\frac12\cdot\hat{MAN}=45^0\)
Xét tứ giác AEPC có \(\hat{EPC}+\hat{EAC}=90^0+90^0=180^0\)
nên AEPC là tứ giác nội tiếp
=>\(\hat{PEC}=\hat{PAC}\)
=>\(\hat{PEC}=45^0\)
Xét ΔPEC vuông tại P có \(\hat{PEC}=45^0\)
nên ΔPEC vuông cân tại P
=>PE=PC
Ta có: \(\hat{PFB}+\hat{PBF}=90^0\) (ΔPBF vuông tại P)
\(\hat{PCE}+\hat{PBQ}=90^0\) (ΔBQC vuông tại Q)
Do đó: \(\hat{BFP}=\hat{BCQ}\)
=>\(\hat{BFP}=45^0\)
Xét ΔPBF vuông tại P có \(\hat{PFB}=45^0\)
nên ΔPBF vuông cân tại P
=>PB=PF
c: ΔEPC cân tại P
mà PI là đường trung tuyến
nên PI⊥EC tại I
ΔPBF cân tại P
mà PK là đường trung tuyến
nên PK⊥BQ tại K
Xét tứ giác PKQI có \(\hat{PKQ}=\hat{PIQ}=\hat{KQI}=90^0\)
nên PKQI là hình chữ nhật
Ai Giải giúp mình 2 bài này với ạ
Mình đang cần gấp, xin cảm ơn.
Bài 3:
a. \(R=R1+R2=15+30=45\Omega\)
b. \(\left\{{}\begin{matrix}I=U:R=9:45=0,2A\\I=I1=I2=0,2A\left(R1ntR2\right)\end{matrix}\right.\)
c. \(\left\{{}\begin{matrix}U1=R1.I1=15.0,2=3V\\U2=R2.I2=30.0,2=6V\end{matrix}\right.\)
Bài 4:
\(I1=U1:R1=6:3=2A\)
\(\Rightarrow I=I1=I2=2A\left(R1ntR2\right)\)
\(U=R.I=\left(3+15\right).2=36V\)
\(U2=R2.I2=15.2=30V\)