Cho hàm số f(x) = ax+b, biết f(-2) = -1 và f(3) = 9. khi đó giá trị của f(1) =

Những câu hỏi liên quan
1.Cho hàm số f(x)=ax+b, biết f(-2)=-1 và f(3)=9. Khi đó giá trị của f(1) bằng..........
2.Cho f(x)=x-1
Giá trị của P=13993.f(\(\frac{1}{2}\)).f(\(\frac{1}{3}\)).f(\(\frac{1}{4}\))....f(\(\frac{1}{1999}\)) là.....
Cho hàm số f(x)=ax+b thỏa mãn đẳng thức
f(f(f(0)))=2 và f(f(f(1)))=29
Khi đó giá trị của a là bao nhiêu?
cho hàm số f(x)= ax+b thỏa mãn các đẳng thức f(f(f(0)))=2 và f(f(f(1)))=29.Khi đó giá trị của a là?
A-1
B-3
C-4
D-5
Cho hàm số \(f\left(x\right)=ax^2+b\), biết \(f\left(-2\right)=-1\) và \(f\left(3\right)=9\)
Khi đó giá trị của \(f\left(1\right)=?\)
tìm giá trị nhỏ nhất của A= / x- 2010/ + ( y+ 2011)^2010 +2011 và giá trị của x, y tương ứng
2, tính : A = 2^12*3^5 - 4^6 * 9^2 / (2^2 * 3)^6 + 8^4 *3^5 - 5^10 *7^3 - 25^5 *49^2/ (125*7)^3 + 5^9 */14^3
3, Cho hàm số y = f(x) = ax^2 + bx +c
Cho biết f(0)= 2010; f(1)=2012 ; f(-1)= 2012. Tính f(-2)
Bài 1:Cho hàm số y=f(x)=x+3/x-2.Tìm số nguyên x để y có giá trị cùng là số nguyên
Bài 2:Cho hàm số y=f(x)=ax+b.Xác định a,b biết :f(1)=3;f(2)=1
Giúp mik nha
a) Cho hàm số
y
f
(
x
)
2
3
x
Tính: f(-2); f(-1); f(0); f(1/2); f(1); f(2); f(3)b) Cho hàm số
y
g
(
x
)
2
3
x
+
3
Tính: g(-2); g(-1); g(0); g(1/2); g(1); g(2); g(3)c) Có nhận xét gì về giá trị của hai hàm số đã cho ở trên khi biến x lấy cùng một giá trị?
Đọc tiếp
a) Cho hàm số
y = f ( x ) = 2 3 x
Tính: f(-2); f(-1); f(0); f(1/2); f(1); f(2); f(3)
b) Cho hàm số
y = g ( x ) = 2 3 x + 3
Tính: g(-2); g(-1); g(0); g(1/2); g(1); g(2); g(3)
c) Có nhận xét gì về giá trị của hai hàm số đã cho ở trên khi biến x lấy cùng một giá trị?
a) Ta có:
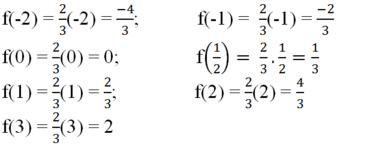
b) Ta có:
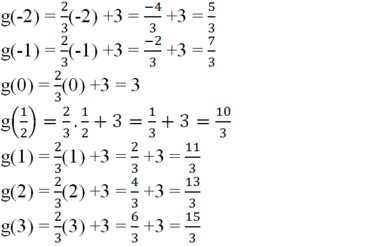
c) Từ kết quả câu a, b ta được bảng sau:

Nhận xét:
- Hai hàm số
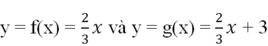
là hai hàm số đồng biến vì khi x tăng thì y cũng nhận được các giá trị tương ứng tăng lên.
- Cùng một giá trị của biến x, giá trị của hàm số y = g(x) luôn luôn lớn hơn giá trị tương ứng của hàm số y = f(x) là 3 đơn vị.
Đúng 0
Bình luận (0)
Câu 1: Cho hàm số y = 2x\(^2\)
a) Hãy lập bảng tính các giá trị f(-5), f(-3), f(0), f(3), f(5)
b) Tìm x biết f(x) = 8, f(x) = 6 - 4\(\sqrt{2}\)
Câu 2: Cho hàm số y = f(x) = \(\dfrac{1}{3}x^2\)
Tìm các giá trị của x, biết rằng \(y=\dfrac{1}{27}\). Cũng câu hỏi tương tự với y = 5
Câu 1:
a)
| \(y=f\left(x\right)=2x^2\) | -5 | -3 | 0 | 3 | 5 |
| f(x) | 50 | 18 | 0 | 18 | 50 |
b) Ta có: f(x)=8
\(\Leftrightarrow2x^2=8\)
\(\Leftrightarrow x^2=4\)
hay \(x\in\left\{2;-2\right\}\)
Vậy: Để f(x)=8 thì \(x\in\left\{2;-2\right\}\)
Ta có: \(f\left(x\right)=6-4\sqrt{2}\)
\(\Leftrightarrow2x^2=6-4\sqrt{2}\)
\(\Leftrightarrow x^2=3-2\sqrt{2}\)
\(\Leftrightarrow x=\sqrt{3-2\sqrt{2}}\)
hay \(x=\sqrt{2}-1\)
Vậy: Để \(f\left(x\right)=6-4\sqrt{2}\) thì \(x=\sqrt{2}-1\)
Đúng 2
Bình luận (0)
Giá trị của a trong công thức của hàm số y=f(x)=ax biết |a|=5 và f(1)>f(2)
Vì f(1)>f(2) => 1.a>2.a . ta dễ dàng thấy a <0 mới thõa mãn 1a>2a . mà trị tuyệt đối của a=5 => a=-5
Đúng 0
Bình luận (0)















