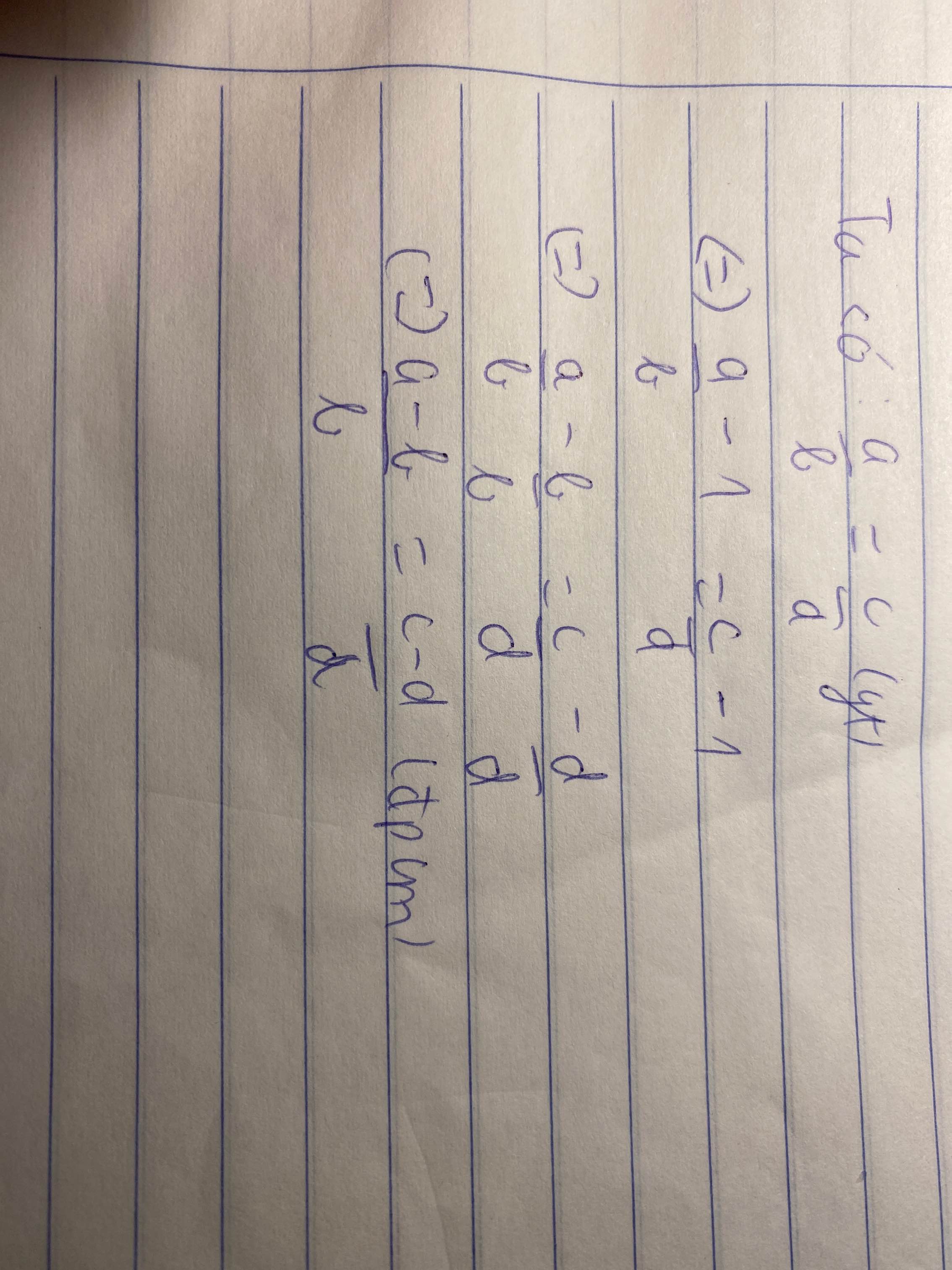giúp tớ  với

Áp dụng t.c dtsbn:

\(\dfrac{a}{b}=\dfrac{c}{d}\Leftrightarrow\dfrac{a}{c}=\dfrac{b}{d}=\dfrac{a+b}{c+d}=\dfrac{a-b}{c-d}\\ \Leftrightarrow\dfrac{a+b}{a-b}=\dfrac{c+d}{c-d}\)

Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{a}{c}=\dfrac{b}{d}=\dfrac{a-b}{c-d}=\dfrac{a+b}{c+d}\)

\(\Leftrightarrow\dfrac{a+b}{a-b}=\dfrac{c+d}{c-d}\)

Đây nhé bạn

Cho \(\frac{a}{b}=\frac{c}{d}\) chứng minh rằng \(\frac{a}{a-b}=\frac{c}{c-d}\)

Có \(\frac{a}{a-b}=\frac{c}{c-d}\Leftrightarrow\frac{a-b}{a}=\frac{c-d}{c}\Leftrightarrow\frac{a}{a}-\frac{b}{a}=\frac{c}{c}-\frac{d}{c}\Leftrightarrow1-\frac{b}{a}=1-\frac{d}{c}\)

\(\Rightarrow\frac{b}{a}=\frac{d}{c}hay\frac{a}{b}=\frac{c}{d}\Rightarrow ad=bc\)

Đề bài cho \(\frac{a}{b}=\frac{c}{d}\) \(\Rightarrow b=c.\) Không thể \(ad=bc\Rightarrow\) Đề sai

chịu

Đề: Cho \(\frac{a}{b}=\frac{c}{d}\). Chứng minh rằng: \(\frac{a}{b}=\frac{a+c}{b+d}=\frac{a-c}{b-d}\). 

Giải: 

Đặt \(\frac{a}{b}=\frac{c}{d}=t\).

\(\frac{a+c}{b+d}=\frac{bt+dt}{b+d}=\frac{t\left(b+d\right)}{b+d}=t\)

\(\frac{a-c}{b-d}=\frac{bt-dt}{b-d}=\frac{t\left(b-d\right)}{b-d}=t\)

Do đó \(\frac{a}{b}=\frac{a+c}{b+d}=\frac{a-c}{b-d}\).

đặt \(\frac{a}{b}=\frac{c}{d}=k\)

=> a=bk, c=dk  =>\(\frac{2a+5b}{3a-4b}=\frac{2bk+5b}{3bk-4b}=\frac{b\left(2k+5\right)}{b\left(3k-4\right)}=\frac{2k+5}{3k-4}\)(1)

=> \(\frac{2c+5d}{3c-4d}=\frac{2dk+5d}{3dk-4d}=\frac{2k+5}{3k-4}\) ( 2)

từ (1)( 2)=> \(\frac{2a+5b}{3a-4b}=\frac{2c+5d}{3c-4d}\)

câu b c/m tg tự 

\(\frac{a}{b}=\frac{c}{d}\Rightarrow ad=bc=ad-bd=bc-bd=d.\left(a-b\right)=b.\left(c-d\right)\Rightarrow\frac{a-b}{b}=\frac{c-d}{d}\)Đúng 100% tick nha

a.d<b.c suy ra \(\frac{a}{b}<\frac{c}{d}\)

Tích chéo nha bạn

\(\frac{a}{2}=\frac{b}{3}=\frac{c}{4}\Rightarrow\frac{q^2}{4}=\frac{b^2}{9}=\frac{2c^2}{32}=\frac{a^2-b^2+2c^2}{4-9+32}=\frac{108}{27}=4\)

=> \(\frac{a^2}{4}=4\Rightarrow a^2=4.4=16\Rightarrow a=+-4\)

=>\(\frac{b^2}{9}=4\Rightarrow b^2=4.9=36\Rightarrow b=+-6\)

=>\(\frac{2c^2}{32}=4\Rightarrow c^2=4.32:2=64\Rightarrow c=+-8\)

Câu 2 :

Ta có : \(\frac{a}{b}=\frac{c}{d}\) \(\Rightarrow\frac{a}{c}=\frac{b}{d}=\frac{a+b}{c+d}=\frac{a-b}{c-d}\)

\(\Rightarrow\frac{a+b}{a-b}=\frac{c+d}{c-d}\)

ghigun