Câu B giúp mình ạ Cảm ơn

Những câu hỏi liên quan
Giúp mình câu b thôi ạ! Mình cảm ơn ạ!
Đọc tiếp
Giúp mình câu b thôi ạ! Mình cảm ơn ạ!
b) Để P nguyên thì \(\sqrt{x}+5⋮3\sqrt{x}-1\)
\(\Leftrightarrow3\sqrt{x}+15⋮3\sqrt{x}-1\)
\(\Leftrightarrow16⋮3\sqrt{x}-1\)
\(\Leftrightarrow3\sqrt{x}-1\in\left\{-1;1;2;4;8;16\right\}\)
\(\Leftrightarrow3\sqrt{x}\in\left\{0;2;3;5;9;17\right\}\)
\(\Leftrightarrow3\sqrt{x}\in\left\{0;3;9\right\}\)
\(\Leftrightarrow\sqrt{x}\in\left\{0;1;3\right\}\)
hay \(x\in\left\{0;1;9\right\}\)
Đúng 1
Bình luận (0)
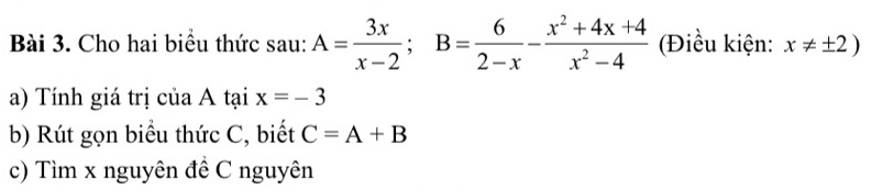
Giúp mình câu b và c với ạ, mình cảm ơn rất nhiều ạ
a: Khi x=3 thì \(A=\dfrac{3\cdot3}{3-2}=9\)
b: C=A+B
\(=\dfrac{3x}{x-2}-\dfrac{6}{x-2}-\dfrac{x^2+4x+4}{x^2-4}\)
\(=\dfrac{3x-6}{x-2}-\dfrac{x+2}{x-2}\)
\(=\dfrac{3x-6-x-2}{x-2}=\dfrac{2x-8}{x-2}\)
c: Để C nguyên thì 2x-4-4 chia hết cho x-2
=>\(x-2\in\left\{1;-1;2;-2;4;-4\right\}\)
=>\(x\in\left\{3;1;4;0;6\right\}\)
Đúng 1
Bình luận (1)
các bạn giúp mình câu b ạ, mình cảm ơn
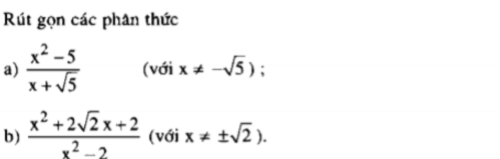
b) \(\dfrac{x^2+2\sqrt{2}x+2}{x^2-2}=\dfrac{\left(x+\sqrt{2}\right)^2}{\left(x-\sqrt{2}\right)\left(x+\sqrt{2}\right)}=\dfrac{x+\sqrt{2}}{x-\sqrt{2}}\)
Đúng 1
Bình luận (0)
a, \(\dfrac{x^2-5}{x+\sqrt{5}}=\dfrac{\left(x-\sqrt{5}\right)\left(x+\sqrt{5}\right)}{x+\sqrt{5}}=x-\sqrt{5}\)
Đúng 1
Bình luận (0)
Mn giúp mình câu B với ạ, mình cảm ơn
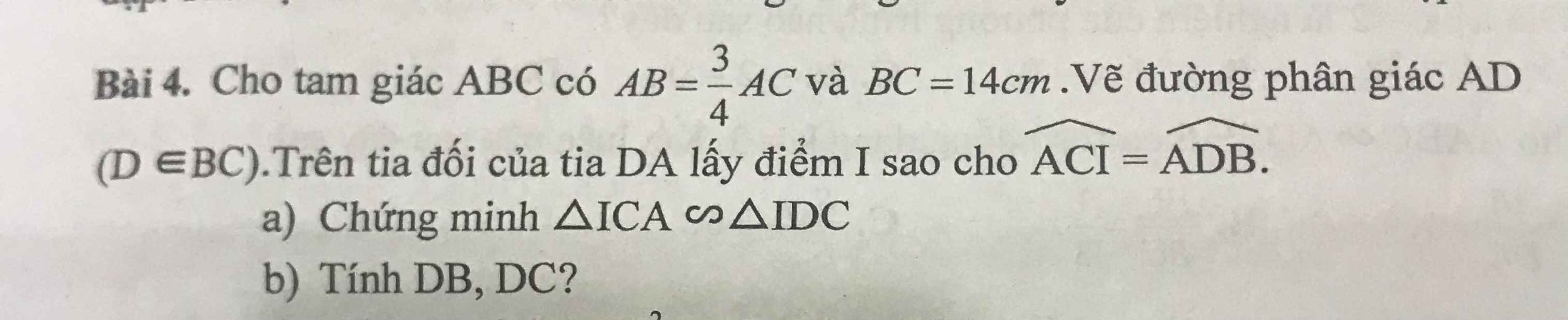
Làm giúp mình câu b với ạ. Mình xin cảm ơn
b: AD là phân giác
=>DB/AB=DC/AC
=>DB/DC=AB/AC=3/4
=>DB/3=DC/4
mà DB+DC=BC=14
nên DB/3=DC/4=14/7=2
=>DB=6cm; DC=8cm
Đúng 0
Bình luận (0)
Làm giúp mình câu b và câu f với ạ. Mình cần gấp, mình cảm ơn trước
Lời giải:
b. Tam giác $ABC$ vuông tại $A$ và $C=45^0$ nên:
$B=90^0-C=90^0-45^0=45^0$
Do đó, tam giác $ABC$ vuông cân tại $A$
$\Rightarrow AC=AB=50$ (cm)
Áp dụng định lý Pitago: $BC=\sqrt{AB^2+AC^2}=\sqrt{50^2+50^2}=50\sqrt{2}$ (cm)
f.
Theo định lý Pitago: $AC=\sqrt{BC^2-AB^2}=\sqrt{7^2-5^2}=2\sqrt{6}$ (cm)
$\sin B=\frac{AC}{BC}=\frac{2\sqrt{6}}{7}$
$\Rightarrow B=44,42^0$
$C=90^0-B=90^0-44,42^0=45,58^0$
Đúng 1
Bình luận (0)
b) Xét ΔABC vuông tại A có \(\widehat{C}=45^0\)(gt)
nên ΔABC vuông cân tại A(Định nghĩa tam giác vuông cân)
Suy ra: \(\widehat{B}=45^0\) và AC=50(cm)
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=50^2+50^2=5000\)
hay \(BC=50\sqrt{2}\left(cm\right)\)
Đúng 0
Bình luận (0)
a) Ta có: ΔABC vuông tại A(gt)
nên \(\widehat{B}+\widehat{C}=90^0\)
hay \(\widehat{B}=60^0\)
Xét ΔABC vuông tại A có
\(AB=AC\cdot\tan30^0\)
\(=100\cdot\dfrac{\sqrt{3}}{3}\)
\(=\dfrac{100\sqrt{3}}{3}\left(cm\right)\)
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=100^2+\left(\dfrac{100\sqrt{3}}{3}\right)^2=\dfrac{40000}{3}\)
hay \(AC=\dfrac{200\sqrt{3}}{3}\left(cm\right)\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
 vẽ giúp mình hình và câu c,b với ạ, mình cảm ơn
vẽ giúp mình hình và câu c,b với ạ, mình cảm ơn
Ai giúp mình câu b phần 2 bài III với cả câu b bài IV với ạ. Mình xin cảm ơn rất rất nhiều ạ.

Bài III.2b.
Phương trình hoành độ giao điểm của \(\left(P\right)\) và \(\left(d\right)\) : \(x^2=\left(m+1\right)x-m-4\)
hay : \(x^2-\left(m+1\right)x+m+4=0\left(I\right)\)
\(\left(d\right)\) cắt \(\left(P\right)\) tại hai điểm nên phương trình \(\left(I\right)\) sẽ có hai nghiệm phân biệt. Do đó, phương trình \(\left(I\right)\) phải có :
\(\Delta=b^2-4ac=\left[-\left(m+1\right)\right]^2-4.1.\left(m+4\right)\)
\(=m^2+2m+1-4m-16\)
\(=m^2-2m-15>0\).
\(\Rightarrow m< -3\) hoặc \(m>5\).
Theo đề bài : \(\sqrt{x_1}+\sqrt{x_2}=2\sqrt{3}\)
\(\Rightarrow\left(\sqrt{x_1}+\sqrt{x_2}\right)^2=\left(2\sqrt{3}\right)^2=12\)
\(\Leftrightarrow x_1+x_2+2\sqrt{x_1x_2}=12\left(II\right)\)
Do phương trình \(\left(I\right)\) có hai nghiệm khi \(m< -3\) hoặc \(m>5\) nên theo định lí Vi-ét, ta có : \(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=-\dfrac{-\left(m+1\right)}{1}=m+1\\x_1x_2=\dfrac{c}{a}=\dfrac{m+4}{1}=m+4\end{matrix}\right.\).
Thay vào \(\left(II\right)\) ta được : \(m+1+2\sqrt{m+4}=12\)
Đặt \(t=\sqrt{m+4}\left(t\ge0\right)\), viết lại phương trình trên thành : \(t^2-3+2t=12\)
\(\Leftrightarrow t^2+2t-15=0\left(III\right)\).
Phương trình \(\left(III\right)\) có : \(\Delta'=b'^2-ac=1^2-1.\left(-15\right)=16>0\).
Suy ra, \(\left(III\right)\) có hai nghiệm phân biệt :
\(\left\{{}\begin{matrix}t_1=\dfrac{-b'+\sqrt{\Delta'}}{a}=\dfrac{-1+\sqrt{16}}{1}=3\left(t/m\right)\\t_2=\dfrac{-b'-\sqrt{\Delta'}}{a}=\dfrac{-1-\sqrt{16}}{1}=-5\left(ktm\right)\end{matrix}\right.\)
Suy ra được : \(\sqrt{m+4}=3\Rightarrow m=5\left(ktm\right)\).
Vậy : Không có giá trị m thỏa mãn đề bài.
Đúng 3
Bình luận (0)
Bài IV.b.
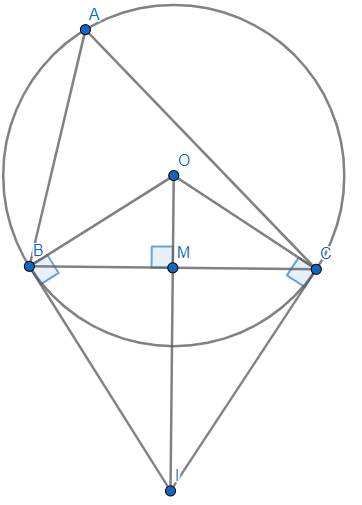
Chứng minh : Ta có : \(OB=OC=R\) nên \(O\) nằm trên đường trung trực \(d\) của \(BC\).
Theo tính chất hai tiếp tuyến cắt nhau thì \(IB=IC\), suy ra \(I\in d\).
Suy ra được \(OI\) là một phần của đường trung trực \(d\) của \(BC\) \(\Rightarrow OI\perp BC\) tại \(M\) và \(MB=MC\).
Xét \(\Delta OBI\) vuông tại \(B\) có : \(MB^2=OM.OI\).
Lại có : \(BC=MB+MC=2MB\)
\(\Rightarrow BC^2=4MB^2=4OM.OI\left(đpcm\right).\)
Tính diện tích hình quạt tròn
Ta có : \(\hat{BAC}=\dfrac{1}{2}sđ\stackrel\frown{BC}\Rightarrow sđ\stackrel\frown{BC}=2.\hat{BAC}=2.70^o=140^o\) (góc nội tiếp).
\(\Rightarrow S=\dfrac{\pi R^2n}{360}=\dfrac{\pi R^2.140^o}{360}=\dfrac{7}{18}\pi R^2\left(đvdt\right)\)
Đúng 2
Bình luận (0)
ai giúp mình với minh cảm ơn nhìu ạ. làm câu nào nào cũng được ạ mình cảm ơn 
Giúp mình câu (b) với ạ ! Cảm ơn bạn nhiều !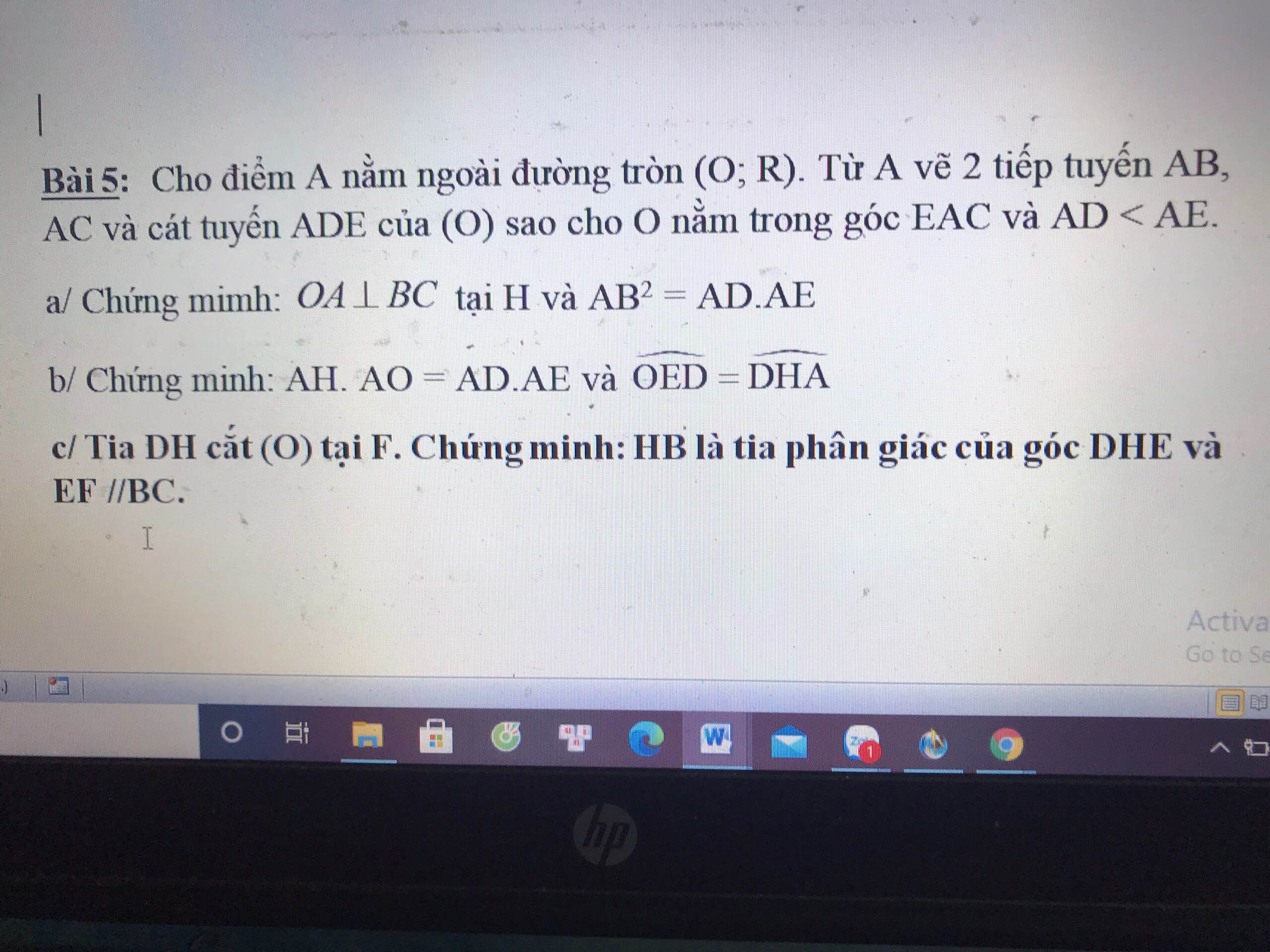
AB là tiếp tuyến nên \(AB\perp OB\) hay tam giác OAB vuông tại B
Áp dụng hệ thức lượng trong tam giác OAB với đường cao BH:
\(AB^2=AH.AO\)
Mà theo câu a. ta có \(AB^2=AD.AE\)
\(\Rightarrow AH.AO=AD.AE\)
//Từ đó ta cũng suy ra \(\dfrac{AH}{AD}=\dfrac{AE}{AO}\)
Xét hai tam giác AHE và ADO có: \(\left\{{}\begin{matrix}\dfrac{AH}{AD}=\dfrac{AE}{AO}\\\widehat{OAE}-chung\end{matrix}\right.\)
\(\Rightarrow\Delta AHE\sim\Delta ADO\left(c.g.c\right)\)
\(\Rightarrow\widehat{DOA}=\widehat{HEA}\)
\(\Rightarrow\) Tứ giác OHDE nội tiếp (2 góc cùng chắn DH bằng nhau)
\(\Rightarrow\widehat{OED}+\widehat{OHD}=180^0\)
Mà \(\widehat{OHD}+\widehat{DHA}=180^0\)
\(\Rightarrow\widehat{OED}=\widehat{DHA}\)
Đúng 0
Bình luận (0)

























