Ba bạn A, B, C mỗi bạn viết ngẫu nhiên lên bảng một số tự nhiên thuộc đoạn [1;21]. Hỏi có bao nhiêu cách viết để ba số được viết ra có tổng bằng 15.
Những câu hỏi liên quan
Ba bạn An, Bình, Cường mỗi bạn viết ngẫu nhiên lên bảng một số tự nhiên thuộc đoạn [1;19].Xác suất để ba số được viết ra có tổng chia hết cho 3 bằng?
A. 2539/6859
B. 2287/6859
C. 109/323
D. 1027/6859
3 bạn A,B,C mỗi bạn viết ngẫu nhiên lên bảng 1 số tự nhiên thuộc đoạn [1;16]. Xác suất để 3 số được viết ra có tổng chia hết cho 3 bằng?
Cho em hỏi cách làm dạng này với ạ :<
Mỗi bạn có 16 cách viết nên số phần tử không gian mẫu là 16^3.
Gọi A là biến cố '3 số được viết ra có tổng chia hết cho 3'
Các số tự nhiên từ 1 đến 16 chia thành 3 nhóm:
Nhóm I gồm các số tự nhiên chia hết cho 3 gồm 5 số.
Nhóm II gồm các số tự nhiên cho 3 dư 1 gồm 6 số.
Nhóm III gồm các số tự nhiên cho 3 dư 2 gồm 5 số.
Để ba số có tổng chia hết cho 3 thì xảy ra các trường hơp sau:
Cả ba bạn viết được số thuộc nhóm I có 5^3 cách.
Cả ba bạn viết được số thuộc nhóm II có 6^3 cách.
Cả ba bạn viết được số thuộc nhóm III có 5^3 cách.
Mỗi bạn viết được một số thuộc một nhóm có 3!×(5×6×5)
=> n(A) = 5^3 + 6^3 + 5^3 + 3!×(5×6×5) = 1366
Vậy P(A) = 1366/16^3
Đúng 1
Bình luận (0)
Ba bạn A , B , C mỗi bạn viết ngẫu nhiên một số tự nhiên thuộc đoạn 1;16 được kí hiệu theo thứ tự là a, b, c rồi lập phương trình bậc hai . Xác suất để phương trình lập được có nghiệm kép là A.
17
2048
B.
5
512
C.
3
512
D.
1
128
Đọc tiếp
Ba bạn A , B , C mỗi bạn viết ngẫu nhiên một số tự nhiên thuộc đoạn 1;16 được kí hiệu theo thứ tự là a, b, c rồi lập phương trình bậc hai . Xác suất để phương trình lập được có nghiệm kép là
A. 17 2048
B. 5 512
C. 3 512
D. 1 128
Ba bạn A , B , C mỗi bạn viết ngẫu nhiên một số tự nhiên thuộc đoạn
1
;
16
được kí hiệu theo thứ tự là a, b, c rồi lập phương trình bậc hai
a
x
2
+
2
b
x
+
c
0
. Xác suất để phương trình lập được có nghiệm kép là A.
17
2048...
Đọc tiếp
Ba bạn A , B , C mỗi bạn viết ngẫu nhiên một số tự nhiên thuộc đoạn 1 ; 16 được kí hiệu theo thứ tự là a, b, c rồi lập phương trình bậc hai a x 2 + 2 b x + c = 0 . Xác suất để phương trình lập được có nghiệm kép là
A. 17 2048
B. 5 512
C. 3 512
D. 1 128
Cho tập S{1,2,..6} Ba bạn A, B, C được mời lên bảng, mỗi bạn viết ngẫu nhiên một tập con của S. Xác suất để các tập con của A, B, C viết được khác rỗng; đôi một không giao nhau và trên bảng có đúng 4 phần tử của S gần nhất với kết quả nào dưới đây ? A. 0,412 B. 0,206 C. 0,432 D. 0,216
Đọc tiếp
Cho tập S={1,2,..6} Ba bạn A, B, C được mời lên bảng, mỗi bạn viết ngẫu nhiên một tập con của S. Xác suất để các tập con của A, B, C viết được khác rỗng; đôi một không giao nhau và trên bảng có đúng 4 phần tử của S gần nhất với kết quả nào dưới đây ?
A. 0,412
B. 0,206
C. 0,432
D. 0,216
Tập S có tất cả 2 6 = 64 tập con. Mỗi bạn có 64 cách viết ngẫu nhiên. Nên số phần tử không gian mẫu bằng 64 3
Ta tìm số cách viết thoả mãn:
Gọi x, y, z là số phần tử có trong các tập con của A, B, C viết lên bảng.
Vì các tập con của ba bạn này viết khác rỗng nên x , y , z ≥ 1
Vì các tập con của ba bạn này đôi một không giao nhau và trên bảng có đúng 4 phần tử của S nên x+y+z=4
Vậy ta có hệ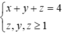 
⇔ ( x ; y ; z ) = 1 ; 1 ; 2 ; 1 ; 2 ; 1 ; 2 ; 1 ; 1
Vậy có tất cả 
cách viết thoả mãn.
Xác suất cần tính bằng 
Chọn đáp án B.
Đúng 0
Bình luận (0)
Cho tập X { 1;2;3;4;5 }. Viết ngẫu nhiên lên bảng hai số tự nhiên, mỗi số gồm 3 chữ số đôi một khác nhau thuộc tập X. Tính xác suất để trong hai số đó có đúng một số có chữ số 5 A.
12
25
B.
12
23
C.
21
25
D.
21
23
Đọc tiếp
Cho tập X = { 1;2;3;4;5 }. Viết ngẫu nhiên lên bảng hai số tự nhiên, mỗi số gồm 3 chữ số đôi một khác nhau thuộc tập X. Tính xác suất để trong hai số đó có đúng một số có chữ số 5
A. 12 25
B. 12 23
C. 21 25
D. 21 23
Số các số tự nhiên có 3 chữ số đôi một khác nhau thuộc tập X là: 5.4.3 = 60.
Trong đó số các số không có mặt chữ số 5 là 4.3.2 = 24 và số các số có mặt chữ số 5 là 60 - 24 = 36.
Gọi A là biến cố hai số được viết lên bảng đều có mặt chữ số 5; B là biến cố hai số được viết lên bảng đều không có mặt chữ số 5.
Rõ ràng A và B xung khắc. Do đó áp dụng quy tắc cộng xác suất ta có:
P A ∪ B = P A + P B = C 36 1 . C 36 1 C 60 1 . C 60 1 + C 24 1 . C 24 1 C 60 1 . C 60 1 = 13 25
Vậy xác suất cần tìm là
P = 1 - P A ∪ B = 1 - 13 25 = 12 25
Đáp án A
Đúng 0
Bình luận (0)
Bạn Xuân viết một số tự nhiên lên bảng. Bạn Hạ viết tiếp vào sau số đó 1994 thì được một số lớn hơn số của Xuân viết là 11993 đơn vị. Bạn Xuân đã viết số tự nhiên nào lên bảng?
Gọi số Xuân viết là A
A1994 = A+11993
10000.A + 1994 = A + 11993
9999.A=9999
A=1
Đúng 0
Bình luận (0)
Cho A = {0, 1, 2, 3, 4, 5, 6}, viết ngẫu nhiên một số tự nhiên có 4 chữ số lên bảng. Tính xác suất để viết được số chia hết cho 4.
A. 1 6
B. 1 7
C. 1 8
D. 1 9
Cho A{0,1,2,3,4,5,6} viết ngẫu nhiên một số tự nhiên có 4 chữ số lên bảng. Tính xác suất để viết được số chia hết cho 4. A. B. C. D.
Đọc tiếp
Cho A={0,1,2,3,4,5,6} viết ngẫu nhiên một số tự nhiên có 4 chữ số lên bảng. Tính xác suất để viết được số chia hết cho 4.
A. 
B. 
C. 
D. 
Đáp án B
Gọi 
là số cần tìm, để số này chia hết cho 4 thì ta phải có 
chia hết cho 4.
Có 
số tự nhiên có 4 chữ số tạo từ 
.
Ta thấy chỉ có các số 
là chia hết cho 4.
Do đó chọn 
có 7 cách, chọn a có 6 cách, chọn b có 7 cách nên có 
Vậy xác suất cần tính là 
Đúng 0
Bình luận (0)
Bạn viết lên bảng 5 số 5, 20 số 20 và 16 số 16. Mỗi số được viết bởi một trong ba màu: xanh, đỏ hoặc vàng. Bạn viết thêm lên bảng tổng của mỗi cặp số trên bảng bởi màu tím. Hỏi có bao nhiêu số màu tím được viết lên bảng?
(A) 848
(B) 816
(C) 820
(D) 804