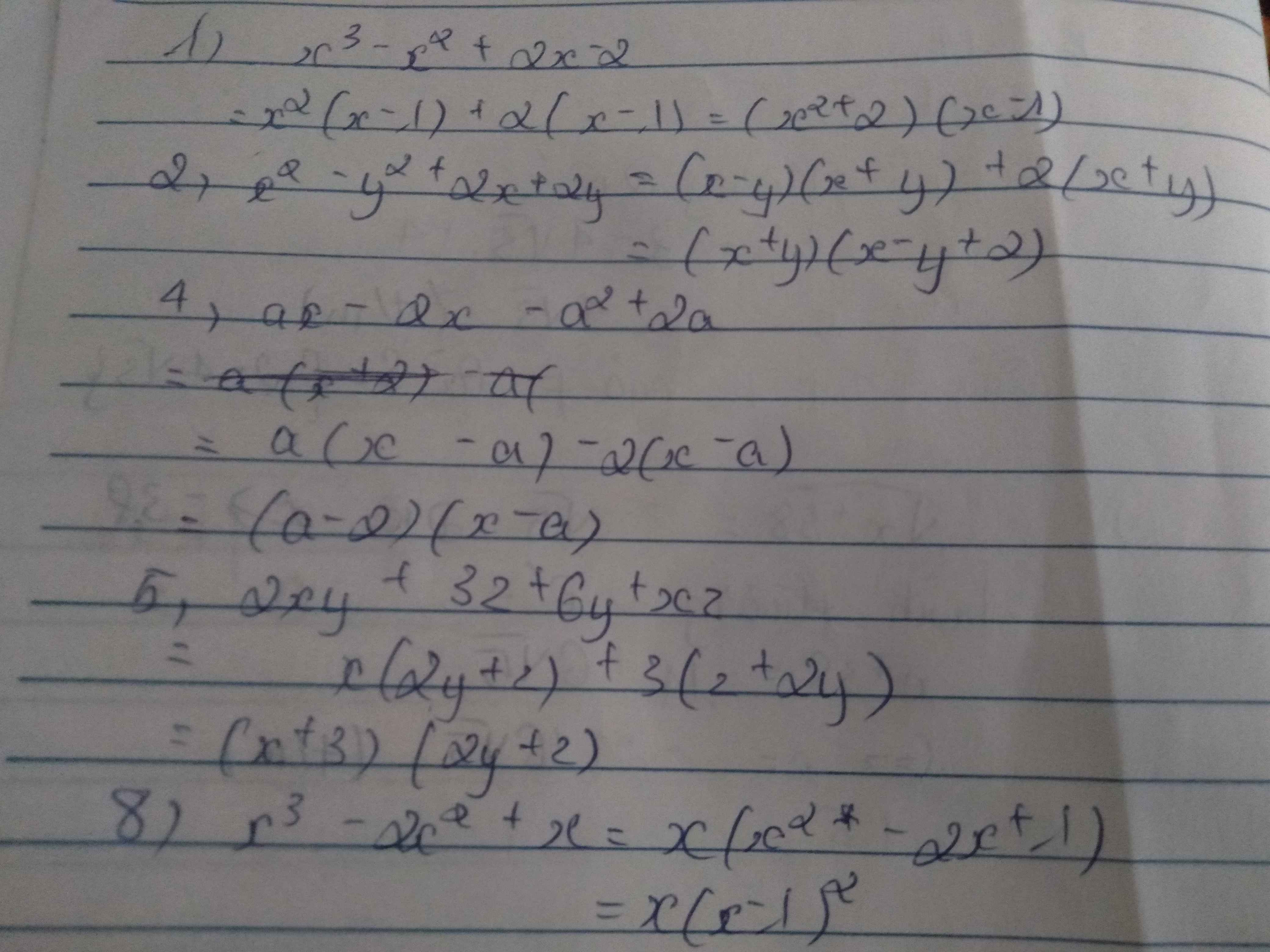Phân tích đa thức thành nhân tử

1: \(x^2-x-y^2-y\)

\(=\left(x^2-y^2\right)-\left(x+y\right)\)

\(=\left(x+y\right)\left(x-y\right)-\left(x+y\right)\)

\(=\left(x+y\right)\left(x-y-1\right)\)

2: \(x^2-y^2+x-y\)

\(=\left(x^2-y^2\right)+\left(x-y\right)\)

\(=\left(x-y\right)\left(x+y\right)+\left(x-y\right)\)

\(=\left(x-y\right)\left(x+y+1\right)\)

3: \(3x-3y+x^2-y^2\)

\(=\left(3x-3y\right)+\left(x^2-y^2\right)\)

\(=3\left(x-y\right)+\left(x-y\right)\left(x+y\right)\)

\(=\left(x-y\right)\left(x+y+3\right)\)

4: \(5x-5y+x^2-y^2\)

\(=\left(5x-5y\right)+\left(x^2-y^2\right)\)

\(=5\left(x-y\right)+\left(x-y\right)\left(x+y\right)\)

\(=\left(x-y\right)\left(5+x+y\right)\)

5: \(x^2-5x-y^2-5y\)

\(=\left(x^2-y^2\right)-\left(5x+5y\right)\)

\(=\left(x-y\right)\left(x+y\right)-5\left(x+y\right)\)

\(=\left(x+y\right)\left(x-y-5\right)\)

6: \(x^2-y^2+2x-2y\)

\(=\left(x^2-y^2\right)+\left(2x-2y\right)\)

\(=\left(x-y\right)\left(x+y\right)+2\left(x-y\right)\)

\(=\left(x-y\right)\left(x+y+2\right)\)

7: \(x^2-4y^2+x+2y\)

\(=\left(x^2-4y^2\right)+\left(x+2y\right)\)

\(=\left(x+2y\right)\left(x-2y\right)+\left(x+2y\right)\)

\(=\left(x+2y\right)\left(x-2y+1\right)\)

8: \(x^2-y^2-2x-2y\)

\(=\left(x^2-y^2\right)-\left(2x+2y\right)\)

\(=\left(x-y\right)\left(x+y\right)-2\left(x+y\right)\)

\(=\left(x+y\right)\left(x-y-2\right)\)

9: \(x^2-4y^2+2x+4y\)

\(=\left(x^2-4y^2\right)+\left(2x+4y\right)\)

\(=\left(x-2y\right)\left(x+2y\right)+2\left(x+2y\right)\)

\(=\left(x+2y\right)\left(x-2y+2\right)\)

nhìu giữ cha !!!!

a.

$12x^3y-24x^2y^2+12xy^3=12xy(x^2-2xy+y^2)=12xy(x-y)^2$
b.

$x^2-6x+xy-6y=(x^2+xy)-(6x+6y)=x(x+y)-6(x+y)=(x-6)(x+y)$
c.

$2x^2+2xy-x-y=2x(x+y)-(x+y)=(x+y)(2x-1)$

d.

$x^3-3x^2+3x-1=(x-1)^3$

e.

$3x^2-3y^2-12x-12y=(3x^2-3y^2)-(12x+12y)$

$=3(x-y)(x+y)-12(x+y)=(x+y)[3(x-y)-12]=3(x-y)(x-y-4)$

f.

$x^2-2xy-x^2+4y^2=4y^2-2xy=2y(2y-x)$

g.

$x^2+2x+1=(x+1)^2$

h. Không phân tích được thành nhân tử

i.

$x^2-2x-3=(x^2-3x)+(x-3)=x(x-3)+(x-3)=(x+1)(x-3)$

j.

$x^2+4x-12=(x^2-2x)+(6x-12)=x(x-2)+6(x-2)=(x-2)(x+6)$

k.

$x^2-8x-9=(x^2+x)-(9x+9)=x(x+1)-9(x+1)=(x+1)(x-9)$

l.

$x^2+x-6=(x^2+3x)-(2x+6)=x(x+3)-2(x+3)=(x-2)(x+3)$

$A=x^2+y^2-6x+4y+20=(x^2-6x+9)+(y^2+4y+4)+7$

$=(x-3)^2+(y+2)^2+7\geq 0+0+7=7$
Vậy $A_{\min}=7$. Giá trị này đạt tại $(x-3)^2=(y+2)^2=0$

$\Leftrightarrow x=3; y=-2$

---------------------

$B=9x^2+y^2+2z^2-18x+4z-6y+30$

$=(9x^2-18x+9)+(y^2-6y+9)+(2z^2+4z+2)+10$

$=9(x^2-2x+1)+(y^2-6y+9)+2(z^2+2z+1)+10$

$=9(x-1)^2+(y-3)^2+2(z+1)^2+10\geq 10$
Vậy $B_{\min}=10$. Giá trị này đạt tại $(x-1)^2=(y-3)^2=(z+1)^2$

$\Leftrightarrow x=1; y=3; z=-1$

$C=x^2+y^2+z^2-xy-yz-xz+3$

$2C=2x^2+2y^2+2z^2-2xy-2yz-2xz+6$

$=(x^2-2xy+y^2)+(y^2-2yz+z^2)+(x^2-2xz+z^2)+6$

$=(x-y)^2+(y-z)^2+(z-x)^2+6\geq 6$

$\Rightarrow C\geq 3$

Vậy $C_{\min}=3$. Giá trị này đạt tại $x-y=y-z=z-x=0$

$\Leftrihgtarrow x=y=z$

--------------------------------------

$D=5x^2+2y^2+4xy-2x+4y+2021$

$=2(y^2+2xy+x^2)+3x^2-2x+4y+2021$

$=2(x+y)^2+4(x+y)+3x^2-6x+2021$
$=2(x+y)^2+4(x+y)+2+3(x^2-2x+1)+2016$

$=2[(x+y)^2+2(x+y)+1]+3(x^2-2x+1)+2016$

$=2(x+y+1)^2+3(x-1)^2+2016\geq 2016$

Vậy $D_{\min}=2016$ khi $x+y+1=x-1=0$

$\Leftrightarrow x=1; y=-2$

$E=x^2-2x+4y^2+4y+2014$

$=(x^2-2x+1)+(4y^2+4y+1)+2012$

$=(x-1)^2+(2y+1)^2+2012$

$\geq 2012$

Vậy $E_{\min}=2012$. Giá trị này đạt tại $x-1=2y+1=0$

$\Leftrightarrow x=1; y=\frac{-1}{2}$

----------------------

$F=5x^2+5y^2+8xy+2y-2x+30$

$=4(x^2+2xy+y^2)+x^2+y^2+2y-2x+30$

$=4(x+y)^2+(x^2-2x+1)+(y^2+2y+1)+28$

$=4(x+y)^2+(x-1)^2+(y+1)^2+28\geq 28$

Vậy $F_{\min}=28$. Giá trị này đạt tại $x+y=x-1=y+1=0$

$\Leftrightarrow x=1; y=-1$

b: \(=\left(x-y\right)^2-4y^2\)

\(=\left(x-y-2y\right)\left(x-y+2y\right)\)

\(=\left(x-3y\right)\left(x+y\right)\)

c: \(=x\left(x-6\right)+y\left(x-6\right)\)

\(=\left(x-6\right)\left(x+y\right)\)

h: \(=\left(x+3\right)\cdot\left(x^2-3x+9\right)-4x\left(x+3\right)\)

\(=\left(x+3\right)\left(x^2-7x+9\right)\)

\(x^2+4xy-4z^2+4y^2\)

\(=x^2+4xy+4y^2-4z^2\)

\(=\left(x+2y\right)^2-4z^2\)

\(=\left(x+2y-2z\right)\left(x+2y+2z\right)\)

\(x^2+2x-15\)

\(=x^2+2x+1-16\)

\(=\left(x+1\right)^2-16\)

\(=\left(x+1-4\right)\left(x+1+4\right)\)

\(=\left(x-3\right)\left(x+5\right)\)

a) Ta có: \(\left(x+2y\right)\left(x^2-2xy+4y^2\right)-\left(x-y\right)\left(x^2+xy+y^2\right)\)

\(=x^3+\left(2y\right)^3-\left(x^3-y^3\right)\)

\(=x^3+8y^3-x^3+y^3\)

\(=9y^3\)

b) Ta có: \(\left(x+1\right)\left(x-1\right)^2-\left(x+2\right)\left(x^2-2x+4\right)\)

\(=\left(x+1\right)\left(x^2-2x+1\right)-\left(x+2\right)\left(x^2-2x+4\right)\)

\(=x^3-2x^2+x+x^2-2x+1-\left(x^3+8\right)\)

\(=x^3-x^2-x+1-x^3-8\)

\(=-x^2-x-7\)

\(l,=5x\left(y^2-2yz+5z\right)\\ m,=\left(x+1\right)^3-27y^3\\ =\left(x+1-3y\right)\left(x^2+2x+1+3xy+3y+9y^2\right)\\ n,=\left(x-3y\right)^2\\ o,=\left(x+2y\right)^3\\ p,=\left(5x+y^2\right)\left(25x^2-5xy^2+y^4\right)\\ q,=\left(x+2y\right)^2-2\left(x-2y\right)+1\\ =\left(x+2y-1\right)^2\)