sin2x + 3sin3x -2cosx -3 =0.Giải pt này giúp mình với

Những câu hỏi liên quan
Giải pt
\(2sin\left(x+\dfrac{\pi}{6}\right)+sinx+2cosx=3\)
\(\left(sin2x+cos2x\right)cosx+2cos2x-sinx=0\)
\(sin2x-cos2x+3sinx-cosx-1=0\)
1.
\(2sin\left(x+\dfrac{\pi}{6}\right)+sinx+2cosx=3\)
\(\Leftrightarrow\sqrt{3}sinx+cosx+sinx+2cosx=3\)
\(\Leftrightarrow\left(\sqrt{3}+1\right)sinx+3cosx=3\)
\(\Leftrightarrow\sqrt{13+2\sqrt{3}}\left[\dfrac{\sqrt{3}+1}{\sqrt{13+2\sqrt{3}}}sinx+\dfrac{3}{\sqrt{13+2\sqrt{3}}}cosx\right]=3\)
Đặt \(\alpha=arcsin\dfrac{3}{\sqrt{13+2\sqrt{3}}}\)
\(pt\Leftrightarrow\sqrt{13+2\sqrt{3}}sin\left(x+\alpha\right)=3\)
\(\Leftrightarrow sin\left(x+\alpha\right)=\dfrac{3}{\sqrt{13+2\sqrt{3}}}\)
\(\Leftrightarrow\left[{}\begin{matrix}x+\alpha=arcsin\dfrac{3}{\sqrt{13+2\sqrt{3}}}+k2\pi\\x+\alpha=\pi-arcsin\dfrac{3}{\sqrt{13+2\sqrt{3}}}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=k2\pi\\x=\pi-2arcsin\dfrac{3}{\sqrt{13+2\sqrt{3}}}+k2\pi\end{matrix}\right.\)
Vậy phương trình đã cho có nghiệm:
\(x=k2\pi;x=\pi-2arcsin\dfrac{3}{\sqrt{13+2\sqrt{3}}}+k2\pi\)
Đúng 0
Bình luận (0)
2.
\(\left(sin2x+cos2x\right)cosx+2cos2x-sinx=0\)
\(\Leftrightarrow2sinx.cos^2x+cos2x.cosx+2cos2x-sinx=0\)
\(\Leftrightarrow\left(2cos^2x-1\right)sinx+cos2x.cosx+2cos2x=0\)
\(\Leftrightarrow cos2x.sinx+cos2x.cosx+2cos2x=0\)
\(\Leftrightarrow cos2x.\left(sinx+cosx+2\right)=0\)
\(\Leftrightarrow cos2x=0\)
\(\Leftrightarrow2x=\dfrac{\pi}{2}+k\pi\)
\(\Leftrightarrow x=\dfrac{\pi}{4}+\dfrac{k\pi}{2}\)
Vậy phương trình đã cho có nghiệm \(x=\dfrac{\pi}{4}+\dfrac{k\pi}{2}\)
Đúng 0
Bình luận (0)
tanx/2cosx-sin2x=0 giải pt
giải PT :
tanx - sin2x - cos2x+ 2(2cosx -1/cosx )= 0
Giải giúp mình pt này với:
sin3x=sin2x
Mik chưa học lớp 11 nên ko trả lời đc sorry nha !! mik mới học lớp 6 thui
Đúng 0
Bình luận (0)
Giúp mình với
Giải pt sau:
\(sin2x\left(2cosx+1\right)-cos2x-2sinx-cosx+1=0\)
Giúp mình với !!!
Giải pt sau :
√3.cotx = 8cos2x.cosx - 1
sin2x.cos2x = sin7x.cos4x
2cosx.(sin2x+sinx - 1) = 1
1)Giải pt bậc hai đối với một hàm số lượng giác:
a. 2 cosxcos2x=1+cos2x+cos3x
b.5(1+cosx)=2+sin^4x-cos^4x
c.sin^4x +cos^4x=sin2x-1/2
2) giải phương trình chứa ẩn dưới mẫu:
Sin2x+2cosx-sinx-1/ tan x+√3=0
Giải: \(\dfrac{sin2x-2cos^2x-5sinx-cosx+4}{2cosx+\sqrt{3}}=0\)
Phương trình: 3sin3x+
3
cos9x 2cosx+4
sin
3
3
x
có số nghiệm trên
0
;
π
2
là A. 2 B. 3 C. 4 D. lớn hơn hoặc bằng 5 nghiệm
Đọc tiếp
Phương trình: 3sin3x+ 3 cos9x= 2cosx+4 sin 3 3 x có số nghiệm trên 0 ; π 2 là
A. 2
B. 3
C. 4
D. lớn hơn hoặc bằng 5 nghiệm
Chọn D
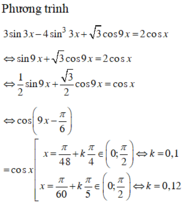
Vậy phương trình có 5 nghiệm thỏa mãn.
Đúng 0
Bình luận (0)
1.2cos2x+2cosx-√2=0
2.cos6x+3sin3x+4=0
1.
\(2\left(2cos^2x-1\right)+2cosx-\sqrt{2}=0\)
\(\Leftrightarrow4cos^2x+2cosx-2-\sqrt{2}=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=\frac{\sqrt{2}}{2}\\cosx=\frac{-1-\sqrt{2}}{2}< -1\left(l\right)\end{matrix}\right.\)
\(\Rightarrow x=\pm\frac{\pi}{4}+k2\pi\)

















