Phân tích đa thức thành nhân tử:
\(a,
7x-6x^2-2\)
\(b,
4x^2+4x-3\)

Những câu hỏi liên quan
Phân tích đa thức thành nhân tử :a)x*4-6x*2+8 b)x*4-5x*2-14 c)4x*4-7x*2+3 d)6x*4+7x*2+2 e)x*4-8x+15 giải chi tiết
Phân tích đa thức thành nhân tử
a) 4x2 - y2 - 1 - 4x
b) 6x2 - 7x - 20
\(a,4x^2-y^2-1-4x\)
\(\Rightarrow\left(4x^2+4x+1\right)-y^2\)
\(=\left(2x+1\right)^2-y^2=\left(2x+1-y\right)\left(2x+1+y\right)\)
\(b,6x^2-7x-20=6x^2-15x+8x-20\)
\(=\left(6x^2-15x\right)+\left(8x-20\right)\)
\(=3x\left(2x-5\right)+4\left(2x-5\right)\)
\(=\left(3x+4\right)\left(2x-5\right)\)
Đúng 0
Bình luận (0)
BT3: Phân tích các đa thức sau thành nhân tử bằng phương pháp cách tách hạng tử. a, x^3 + 4x^2 - 21x b, 5x^3 + 6x^2 + x c, x^3 - 7x + 6 d, 3x^3 + 2x - 5
a) \(x^3+4x^2-21x\)
\(=x\left(x^2+4x-21\right)\)
\(=x\left(x^2-3x+7x-21\right)\)
\(=x\left[x\left(x-3\right)+7\left(x-3\right)\right]\)
\(=x\left(x-3\right)\left(x+7\right)\)
b) \(5x^3+6x^2+x\)
\(=x\left(5x^2+6x+1\right)\)
\(=x\left(5x^2+5x+x+1\right)\)
\(=x\left[5x\left(x+1\right)+\left(x+1\right)\right]\)
\(=x\left(x+1\right)\left(5x+1\right)\)
c) \(x^3-7x+6\)
\(=x^3+2x^2-3x-2x^2-4x+6\)
\(=x\left(x^2+2x-3\right)-2\left(x^2+2x-3\right)\)
\(=\left(x-2\right)\left(x^2+2x-3\right)\)
\(=\left(x-2\right)\left(x-1\right)\left(x+3\right)\)
d) \(3x^3+2x-5\)
\(=3x^3+3x^2+5x-3x^2-3x-5\)
\(=x\left(3x^2+3x+5\right)-\left(3x^2+3x+5\right)\)
\(=\left(x-1\right)\left(3x^2+3x+5\right)\)
Đúng 1
Bình luận (0)
Phân tích đa thức thành nhân tử
4x\(^4\)-4x\(^3\)-7x\(^2\)-4x+4
\(4x^4-8x^3+4x^3-8x^2+x^2-2x-2x+4\\ =4x^3\left(x-2\right)+4x^2\left(x-2\right)+x\left(x-2\right)-2\left(x-2\right)\\ =\left(x-2\right)\left(4x^3+4x^2+x-2\right)\\ =\left(x-2\right)\left(4x^3-2x^2+6x^2-3x+4x-2\right)\\ =\left(x-2\right)\left[2x^2\left(2x-1\right)+3x\left(2x-1\right)+2\left(2x-1\right)\right]\\ =\left(x-2\right)\left(2x-1\right)\left(2x^2+3x-2\right)\)
Đúng 0
Bình luận (0)
Phân tích đa thức thành nhân tử:
a) \(x^3+4x^2-29x+24\)
b) \(x^4+6x^3+7x^2-6x+1\)
a) nhận xét hệ số : 1 + 4 - 29 + 24 = 0
=> x3 + 4x2 - 29x + 24 = x2(x-1) + 5x(x-1) - 24(x-1)
= (x-1)(x2+5x-24) = (x-1)(x-3)(x+8)
b) ...
Đúng 0
Bình luận (0)
a) \(x^3+4x^2-29x+24\)=\(\left(x+8\right)\left(x^2-4x+3\right)\)=\(\left(x+8\right)\left(x^2-x-3x+3\right)\)=\(\left(x+8\right)\left(x-1\right)\left(x-3\right)\)
b) \(x^4+6x^3+7x^2-6x+1\)=\(x^4+3x^3-x^2+3x^3+9x^2-3x-x^2-3x+1\)=\(x^2\left(x^2+3x-1\right)+3x\left(x^2+3x-1\right)-\left(x^2+3x-1\right)\)=\(\left(x^2+3x-1\right)\left(x^2+3x-1\right)\)=\(\left(x^2+3x-1\right)^2\)
Đúng 0
Bình luận (0)
phân tích đa thức thành nhân tử
1)x^2+5x-6
b)7x-6x^2-2
c)x^2+4x+3
d)2x^2+5x-3
a) \(x^2+5x-6=x^2-x+6x-6=x.\left(x-1\right)+6.\left(x-1\right)=\left(x+6\right)\left(x-1\right)\)
b) \(7x-6x^2-2=3x-6x^2-2+4x=3x.\left(1-2x\right)-2.\left(1-2x\right)=\left(1-2x\right)\left(3x-2\right)\)
c)\(x^2+4x+3=x^2+x+3x+3=x.\left(x+1\right)+3.\left(x+1\right)=\left(x+3\right)\left(x+1\right)\)
d) \(2x^2+5x-3=2x^2-x+6x-3=x.\left(2x-1\right)+3.\left(2x-1\right)=\left(x+3\right)\left(2x-1\right)\)
Đúng 0
Bình luận (0)
Phân tích các đa thức sau thành nhân tử:
a) x²-7x+6
x-3√3x-12√3 b)x2+4x-2
Lời giải:
a.
$x^2-7x+6=(x^2-x)-(6x-6)=x(x-1)-6(x-1)=(x-1)(x-6)$
b.
$x-3\sqrt{3}x-12\sqrt{3}$ không phân tích được thành nhân tử
c.
$x^2+4x-2$ không phân tích được thành nhân tử với các hệ số nguyên.
Đúng 1
Bình luận (0)
Phân tích các đa thức sau thành nhân tử:a) 4
x
2
- 4x + 1; b) 16
y
3
- 2
x
3
- 6x(x + 1) - 2;c) 2
x
2
+7x + 5; d)
x
2
- 6xy - 25
z
2
+9
y
2
Đọc tiếp
Phân tích các đa thức sau thành nhân tử:
a) 4 x 2 - 4x + 1; b) 16 y 3 - 2 x 3 - 6x(x + 1) - 2;
c) 2 x 2 +7x + 5; d) x 2 - 6xy - 25 z 2 +9 y 2
phân tích đa thức thành nhân tử a. 27x^3-8 b. 8x^3+12x^2+6x+1 c.(2y-1)^2-4x^2+4x-1
a) \(27x^3-8=\left(3x-2\right)\left(9x^2+6x+4\right)\)
b) \(8x^3+12x^2+6x+1=\left(2x+1\right)^3\)
c) \(\left(2y-1\right)^1-4x^2+4x-1=\left(2y-1\right)^2-\left(2x-1\right)^2=\left(2y-1-2x+1\right)\left(2y-1+2x-1\right)\)
\(=\left(2y-2x\right)\left(2y+2x-2\right)=4\left(y-x\right)\left(y+x-1\right)\)
Đúng 0
Bình luận (0)
Phân tích đa thức thành nhân tử 3x^3+4x^2-7x
Ta có:x(3x2+4x-7)=x[(3x2-3x)+(7x-7)]=x[3x(x-1)+7(x-1)]=x(x-1)(3x+7)
Đúng 1
Bình luận (1)



















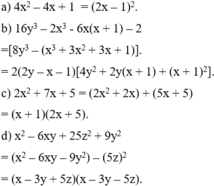

 k cho tui nha
k cho tui nha



