a) (2x-3)2=16
Yêu cầu: Giải 2 thành trường hợp
TH1: (2x-3)2=(4)2
TH2: (2x-3)2=(-4)2

Những câu hỏi liên quan
Giải phương trình ( giải theo trường hợp phương trình chứa biến ở mẫu)
a) 3 phần x-2 = 2x-1 phần x-2 -x
b) x+2 phần x = 2x+3 phần 2x-4
a: \(\Leftrightarrow\dfrac{3}{x-2}=\dfrac{2x-1}{x-2}-\dfrac{x\left(x-2\right)}{x-2}\)
=>3=2x-1-x^2+2x
=>3=-x^2+4x-1
=>x^2-4x+1+3=0
=>x^2-4x+4=0
=>x=2(loại)
b: =>(x+2)(2x-4)=x(2x+3)
=>2x^2-4x+4x-8=2x^2+3x
=>3x=-8
=>x=-8/3(nhận)
Đúng 0
Bình luận (0)
GIẢI GIÚP MÌNH GẤP NHA CẢM ƠN CÁC BẠN NHÌU !!!!!!
Phân tích các đa thúc sau thành nhân tử
a. (x^2 + y^2-5)- 4-x^y^2-16xy-16
b.(ab-1)^2+(a+b)^2
c.x^3+2x^2+2x+1
d.x^3-4x^2+12x-27
e.x^4-2x^3+2x-1
f.x^4+2x^3+2x^2+2x+1
g.x^2-2x-4y^2-4y
h.x^4+2x^3-4x-4
i.x^2(1-x^2)-4-4x^2
k.x^2+y^2-x^2y^2+xy-x-y
giải pt:
a)2x+1/6 - x-2/4= 3-2x/3 -x
b)2x/x-1 + 4/x^2+2x-3 = 2x-5/x+3
Xem chi tiết
phân tích đa thức thành nhân tử
a) 4x (a-b) +6xy(b-a)
b) (6x+3) - ( 2x-5) (2x+1)
c) 4 ( x-3)^2 +2x (3-x)
d) x^4 +2x^2 -4x-4
e) 2x (x+y) -x -y
g)( 3x-1 )^2 - (x+3)^2
a) \(4x\left(a-b\right)+6xy\left(b-a\right)\)
\(=4x\left(a-b\right)-6xy\left(a-b\right)\)
\(=\left(4x-6xy\right)\left(a-b\right)\)
\(=2x\left(2-3y\right)\left(a-b\right)\)
Đúng 1
Bình luận (0)
b) \(\left(6x+3\right)-\left(2x-5\right)\left(2x+1\right)\)
\(=3\left(2x+1\right)-\left(2x-5\right)\left(2x+1\right)\)
\(=\left(3-2x+5\right)\left(2x+1\right)\)
\(=\left(8-2x\right)\left(2x+1\right)\)
\(=2\left(4-x\right)\left(2x+1\right)\)
Đúng 1
Bình luận (0)
g: \(\left(3x-1\right)^2-\left(x+3\right)^2\)
\(=\left(3x-1-x-3\right)\left(3x-1+x+3\right)\)
\(=\left(2x-4\right)\left(4x+2\right)\)
\(=4\left(x-2\right)\left(2x+1\right)\)
Đúng 0
Bình luận (0)
Phân tích thành nhân tử :
a) x3 - 4x2 + 12x - 27
b) x3 + 2x2 + 2x + 1
c) x4 - 2x3 + 2x - 1
d) x4 + 2x3 + 2x2 + 2x + 1
Ai giải thì giải hết giúp mình đi ạ!
a, \(x^3-4x^2+12x-27\) \(=x^3-3x^2-x^2+3x+9x-27\)
= \(x^2\left(x-3\right)-x\left(x-3\right)+9\left(x-3\right)\) \(=\left(x-3\right)\left(x^2-x+9\right)\)
b, \(x^3+2x^2+2x+1\) \(=x^3+x^2+x^2+x+x+1\)
= \(x^2\left(x+1\right)+x\left(x+1\right)+x+1=\) \(\left(x+1\right)\left(x^2+x+1\right)\)
c, \(x^4-2x^3+2x-1=\) \(x^4-x^3-x^3+x^2-x^2+x+x-1\)
= \(x^3\left(x-1\right)-x^2\left(x-1\right)-x\left(x-1\right)+x-1\)
= \(\left(x-1\right)\left(x^3-x^2-x+1\right)\)
d, \(x^4+2x^3+2x^2+2x+1=\) \(x^4+x^3+x^3+x^2+x^2+x+x+1\)
= \(x^3\left(x+1\right)+x^2\left(x+1\right)+x\left(x+1\right)+x+1\)
= \(\left(x+1\right)\left(x^3+x^2+x+1\right)\)
Đúng 0
Bình luận (0)
Ta có : x3 - 4x2 + 12x - 27
= (x3 - 27) - (4x2 - 12x)
= (x - 3)(x2 + 3x + 9) - 4x(x - 3)
= (x - 3)(x2 + 3x + 9 - 4x)
= (x - 3)(x2 - x + 9)
b) https://olm.vn/hoi-dap/question/1004349.html tôi tự coppy tôi
Đúng 0
Bình luận (0)
1. Phân tích đa thức thành nhân tử:
a. (ab-1)^2+(a+b)^2
b. x^3+2x^2+2x+1
c. x^3-sx^2+12x-27
d. x64-2x^3+2x-1
e. x^4+2x^3+2x^2+2x+1
f. x^2-2x-4y^2-4y
g. x^4+2x^3-4x-4
h. x^2(1-x^2)-4-4x^2
i. (1+2x)(1-2x)-x(x+2)(x-2)
j. x^2+y^2-x^2.y^2+xy-x-y
2.Phân tích đa thức thành nhân tử:
a. a(b^2+c^2+bc)+b(c^2+a^2+ac)+c(a^2+b^2+ab)
b.(a+b+c)(ab+bc+ca)-abc
c. a(a+2b)^3-b(2a+b)^3
Giải phương trình
a
)
2
x
+
3
x
-
4
2
x
-
1
x
+
2
-
27
b
)
x
2
-
4
-
x
+
5...
Đọc tiếp
Giải phương trình
a ) 2 x + 3 x - 4 = 2 x - 1 x + 2 - 27
b ) x 2 - 4 - x + 5 2 - x = 0
c ) x + 2 x - 2 - x - 2 x + 2 = 4 x 2 - 4
d ) x + 1 x - 1 - x + 2 x + 3 + 4 x 2 + 2 x - 3 = 0
a) 2(x + 3)(x – 4) = (2x – 1)(x + 2) – 27
⇔ 2(x2 – 4x + 3x – 12) = 2x2 + 4x – x – 2 – 27
⇔ 2x2 – 2x – 24 = 2x2 + 3x – 29
⇔ -2x – 3x = 24 – 29
⇔ - 5x = - 5 ⇔ x = -5/-5 ⇔ x = 1
Tập nghiệm của phương trình : S = {1}
b) x2 – 4 – (x + 5)(2 – x) = 0
⇔ x2 – 4 + (x + 5)(x – 2) = 0 ⇔ (x – 2)(x + 2 + x + 5) = 0
⇔ (x – 2)(2x + 7) = 0 ⇔ x – 2 = 0 hoặc 2x + 7 = 0
⇔ x = 2 hoặc x = -7/2
Tập nghiệm của phương trình: S = {2; -7/2 }
c) ĐKXĐ : x – 2 ≠ 0 và x + 2 ≠ 0 (khi đó : x2 – 4 = (x – 2)(x + 2) ≠ 0)
⇔ x ≠ 2 và x ≠ -2
Quy đồng mẫu thức hai vế :
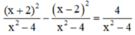
Khử mẫu, ta được : x2 + 4x + 4 – x2 + 4x – 4 = 4
⇔ 8x = 4 ⇔ x = 1/2( thỏa mãn ĐKXĐ)
Tập nghiệm của phương trình : S = {1/2}
d) ĐKXĐ : x – 1 ≠ 0 và x + 3 ≠ 0 (khi đó : x2 + 2x – 3 = (x – 1)(x + 3) ≠ 0)
⇔ x ≠ 1 và x ≠ -3
Quy đồng mẫu thức hai vế :
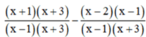
![]()
Khử mẫu, ta được : x2 + 3x + x + 3 – x2 + x – 2x + 2 + 4 = 0
⇔ 3x = -9 ⇔ x = -3 (không thỏa mãn ĐKXĐ)
Tập nghiệm của phương trình : S = ∅
Đúng 0
Bình luận (0)
\(2\left(x+3\right)\left(x-4\right)=\left(2x-1\right)\left(x+2\right)-27\)
\(< =>2\left(x^2-x-12\right)=2x^2+3x-2-27\)
\(< =>2x^2-2x-24=2x^2+3x-2-27\)
\(< =>5x=-24+29=5\)
\(< =>x=\frac{5}{5}=1\)
\(x^2-4-\left(x+5\right)\left(2-x\right)=0\)
\(< =>\left(x-2\right)\left(x+2\right)+\left(x+5\right)\left(x-2\right)=0\)
\(< =>\left(x-2\right)\left(x+2+x+5\right)=0\)
\(< =>\left(x-2\right)\left(2x+7\right)=0\)
\(< =>\orbr{\begin{cases}x-2=0\\2x+7=0\end{cases}}< =>\orbr{\begin{cases}x=2\\x=-\frac{7}{2}\end{cases}}\)
Xem thêm câu trả lời
Xác định các số nguyên sao cho:
a. Đa thức: x^4+x^3+2x^2-7x-5 phân tích thành tích của 2 đa thức: x^2+2x+5 và x^2+bx+c
b. Đa thức: x^4-2x^3+2x^2-2x+a phân tích thành tích của 2 đa thức: x^2-2x+1 và x^2+bx+c
Giải những phương trình sau a, 1/x^2-2x+2 +2/x^2-2x+3 = 6/x^2-2x+4
b,x^2-2x+3|x-2|<3
Phân tích đa thức thành nhân tử
a, x^4-5x^2+4
b, 45+x^3-5x^2-9x
c, x^4-2x^3-2x^2-2x-3
c. \(x^4-2x^3-2x^2-2x-3=x^3\left(x-3\right)+x^2\left(x-3\right)+x\left(x-3\right)+x-3\)
\(=\left(x-3\right)\left(x^3+x^2+x+1\right)=\left(x-3\right)\left(x+1\right)\left(x^2+1\right)\)
Đúng 0
Bình luận (0)
























