Giải giúp với ạ.
Giải bất phương trình 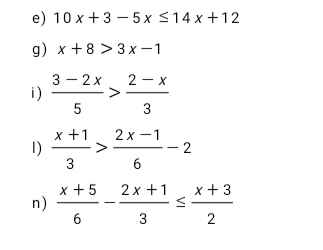

Những câu hỏi liên quan
giải chi tiết giúp em với ạ, em cảm ơn ^^ Giải bất phương trình sau

ĐK: \(x\ge0\)
Dễ thấy \(1-\sqrt{2\left(x^2-x+1\right)}\le1-\sqrt{2}< 0\)
Khi đó bất phương trình tương đương:
\(x-\sqrt{x}\le1-\sqrt{2\left(x^2-x+1\right)}\)
\(\Leftrightarrow\sqrt{x}-\dfrac{1}{\sqrt{x}}-1+\sqrt{2\left(x+\dfrac{1}{x}-1\right)}\le0\)
\(\Leftrightarrow\sqrt{x}-\dfrac{1}{\sqrt{x}}-1+\sqrt{2\left(\sqrt{x}-\dfrac{1}{\sqrt{x}}\right)^2+2}\le0\)
\(\Leftrightarrow t-1+\sqrt{2t^2+2}\le0\)
Đúng 1
Bình luận (1)
Giải bất phương trình \(\sqrt{ }\)X² + 61x ≤ 4x + 2 Giúp e với ạ thanks
Giúp e với ạ Giải bất phương trình: (x ^ 2 - 3x + 2)/(9 - x ^ 2) >0
\(\Leftrightarrow\dfrac{\left(x-1\right)\left(x-2\right)}{\left(3-x\right)\left(3+x\right)}>0\)
Bảng xét dấu:
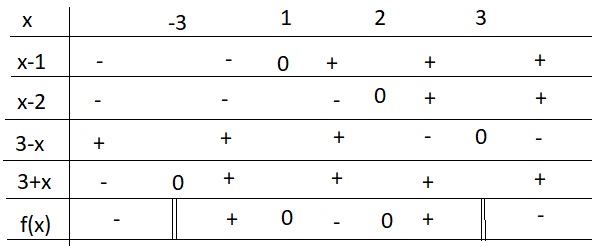
Từ bảng xét dấu ta có nghiệm của BPT là: \(x\in\left(-3;1\right)\cup\left(2;3\right)\)
Đúng 2
Bình luận (0)
Giúp e câu c với ạ. Giải bất phương trình sử dụng dấu nhị thức bậc nhất
Do \(x^2+x+1=\left(x+\dfrac{1}{2}\right)^2+\dfrac{3}{4}>0;\forall x\) nên BPT tương đương:
\(-3\left(x^2+x+1\right)\le x^2-3x-1\le3\left(x^2+x+1\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2-3x-1\ge-3x^2-3x-3\\x^2-3x-1\le3x^2+3x+3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}4x^2\ge-2\left(luôn-đúng\right)\\2x^2+6x+4\ge0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x\ge-1\\x\le-2\end{matrix}\right.\)
Đúng 5
Bình luận (0)
Giải bất phương trình:
\(\dfrac{3x+5}{3}>-2\) : \(\dfrac{6x+5}{2}\)
Giúp mình với ạ.
=>\(\dfrac{3x+5}{3}>\dfrac{-4}{6x+5}\)
=>\(\dfrac{18x^2+15x+30x+25+12}{3\left(6x+5\right)}>0\)
=>\(\dfrac{18x^2+45x+37}{3\left(6x+5\right)}>0\)
=>6x+5>0
=>x>-5/6
Đúng 0
Bình luận (1)
Giải các bất phương trình sau ( biểu diễn trục số ) 1) | 4x-1 | = 5-x Giúp em với ạ
\(\left|4x-1\right|=5-x\)
\(\Leftrightarrow\left[{}\begin{matrix}4x-1=5-x\left(x\ge\dfrac{1}{4}\right)\\4x-1=x-5\left(x< \dfrac{1}{4}\right)\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{6}{5}\left(nhận\right)\\x=-\dfrac{4}{3}\left(nhận\right)\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Giải bất phương trình sau ( với a là một số cho trước ):
( a - 1 )x +2a +1>0 với a>1
Giúp mình với ạ !
\(\left(a-1\right)x+2a+1>0\)
=>\(\left(a-1\right)x>-2a-1\)
=>\(x>\dfrac{-2a-1}{a-1}\)
Đúng 0
Bình luận (0)
giải phương trình và bất phương trình sau:
a, \(\dfrac{3}{x-1}=\dfrac{4}{x+1}\)
b,(x-1).(x-3)=0
c, 2(x-1)+x=0
mọi người giúp mình với ạ
a: =>3x+3=4x-4
=>-x=-7
hay x=7(nhận)
b: (x-1)(x-3)=0
=>x-1=0 hoặc x-3=0
=>x=1 hoặc x=3
c: 2(x-1)+x=0
=>2x-2+x=0
=>3x-2=0
hay x=2/3
Đúng 1
Bình luận (0)
a, ĐKXĐ : x ≠ 1 ; x ≠ -1
\(\Rightarrow3\left(x+1\right)=4\left(x-1\right)\)
\(\Leftrightarrow3x+3=4x-4\)
\(\Leftrightarrow-x=-7\)
\(\Leftrightarrow x=7\left(N\right)\)
b,
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=3\end{matrix}\right.\)
c,
\(\Leftrightarrow2x-2+x=0\)
\(\Leftrightarrow3x=2\)
\(\Leftrightarrow x=\dfrac{2}{3}\)
Đúng 1
Bình luận (0)
cho \(\sqrt{x+3}-\sqrt{7-x}>\sqrt{2x-8}\) số nghiệm nguyên của bất phương trình là:
giải giúp em với ạ
\(\sqrt{x+3}-\sqrt{7-x}>\sqrt{2x-8}\)
⇔ \(\sqrt{x+3}>\sqrt{7-x}+\sqrt{2x-8}\)
⇔ \(\left\{{}\begin{matrix}4\le x\le8\\x+3>7-x+2x-8+2\sqrt{\left(7-x\right)\left(2x-8\right)}\end{matrix}\right.\)
⇔ \(\left\{{}\begin{matrix}4\le x\le8\\x+3>x-1+2\sqrt{\left(7-x\right)\left(2x+8\right)}\end{matrix}\right.\)
⇔ \(\left\{{}\begin{matrix}4\le x\le8\\4>2\sqrt{\left(7-x\right)\left(2x+8\right)}\end{matrix}\right.\)
⇔ \(\left\{{}\begin{matrix}4\le x\le8\\\sqrt{\left(7-x\right)\left(2x-8\right)}< 2\end{matrix}\right.\)
⇔ \(\left\{{}\begin{matrix}4\le x\le8\\-2x^2+22x-56< 2\end{matrix}\right.\)
⇔ \(\left\{{}\begin{matrix}4\le x\le8\\\left[{}\begin{matrix}x>\dfrac{11+\sqrt{5}}{2}\\x< \dfrac{11-\sqrt{5}}{2}\end{matrix}\right.\end{matrix}\right.\)
⇔ \(\left[{}\begin{matrix}4\le x< \dfrac{11-\sqrt{5}}{2}\\\dfrac{11+\sqrt{5}}{2}< x\le8\end{matrix}\right.\)
Các giá trị nguyên của x thỏa mãn là S = {4 ; 7 ; 8}
Đúng 1
Bình luận (0)
Ấy chết sai điều kiện XĐ rồi, bạn sửa lại điều kiện thôi nhé
Đúng 1
Bình luận (0)
e)12-3x/2x+6>3
(Giải bất phương trình rồi biểu diễn tập nghiệm trên trục số)
mn giúp mình với ạ
e: \(\dfrac{12-3x}{2x+6}-3>0\)
\(\Leftrightarrow\dfrac{12-3x-6x-18}{2x+6}>0\)
\(\Leftrightarrow\dfrac{-9x+6}{2x+6}>0\)
\(\Leftrightarrow\dfrac{3x-2}{x+3}< 0\)
=>-3<x<2/3
Đúng 1
Bình luận (1)



















