Bạn cần viết đề bằng công thức toán (biểu tượng $\sum$ bên trái khung soạn thảo) để được hỗ trợ tốt hơn.

thx ban

Để \(\frac{2a+2b}{ab+1}\) là bình phương của 1 số nguyên thì 2a + 2b chia hết cho ab + 1; mà ab + 1 chia hết cho 2a + 2b => ab + 1 = 2b + 2a
=> \(\frac{2a+2b}{ab+1}\)=1 = 1²

Ta có:

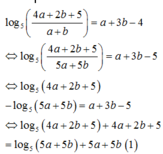
Xét hàm số

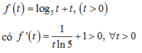
 Hàm số f t  đồng biến trên 0 ; + ∞

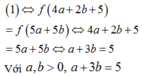
 ta có:

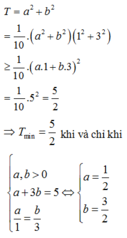
Chọn: D

Đáp án B

Ta có: log 5 4 a + 2 b + 5 a + b = a + 3 b − 4  

⇔ log 5 4 a + 2 b + 5 + 4 a + 2 b + 5 = log 5 5 a + 5 b + 5 a + 5 b  

Xét hàm số f t = log 5 t + t t > 0 ⇒ f t  đồng biến trên 0 ; + ∞  

Do đó f 4 a + 2 b + 5 = f 5 a + 5 b ⇔ 4 a + 2 b + 5 = 5 a + 5 b  

⇔ a + 3 b = 5 ⇒ T = 5 − 3 b 2 + b 2 = 10 b 2 − 30 b + 25 = 10 b − 3 2 2 + 5 2 ≥ 5 2