Xác định hệ số a,b,c ; biết:
(x2+cx+2)(ax+b)= x3+x2-2 với mọi x
(ay2+by+c)(y+3)= y3+2y2-3y với mọi y
(z2-z+1)(az2+bz+c)=2z4-z3+2z2+1 với mọi z
Mn giúp e với ạ
Những câu hỏi liên quan
Cho hai đa thức biến x : A = ax^2 - 3x - 18 và B = 1 + 4x - 7x^2
a) Xác định bậc , hệ số cao nhất , hệ số tự do của B
b) Xác định hệ số a xuất hiện ở đa thức A , biết rằng A có một nghiệm là 2
c) Với a tìm được . tìm đa thức C sao cho C + B = A
a: Bậc là 2
Hệ số cao nhất là -7
Hệ số tự do là 1
b: Thay x=2 vào A=0, ta được:
\(a\cdot2^2-3\cdot2-18=0\)
\(\Leftrightarrow4a=24\)
hay a=6
c: Ta có: C+B=A
nên C=A-B
\(=6x^2-3x-18-1-4x+7x^2\)
\(=13x^2-7x-19\)
Đúng 1
Bình luận (0)
Cho phương trình 3x2 + 7x + 4 = 0.
Xác định các hệ số a, b, c rồi tính a - b + c.
a = 3; b = 7; c = 4
⇒ a + b + c = 3 - 7 + 4 = 0
Đúng 0
Bình luận (0)
Cho phương trình 2x2 – 5x + 3 = 0.
Xác định các hệ số a, b, c rồi tính a + b + c.
a = 2; b = -5; c = 3
⇒ a + b + c = 2 - 5 + 3 = 0
Đúng 0
Bình luận (0)
Không giải phương trình, hãy xác định các hệ số a, b, c, tính biệt thức Δ và xác định số nghiệm của mỗi phương trình sau: 7 x 2 - 2 x + 3 = 0
Phương trình bậc hai: 7x2 – 2x + 3 = 0
Có: a = 7; b = -2; c = 3; Δ = b2 – 4ac = (-2)2 – 4.7.3 = -80 < 0
Vậy phương trình vô nghiệm.
Đúng 0
Bình luận (0)
Không giải phương trình, hãy xác định các hệ số a, b, c, tính biệt thức Δ và xác định số nghiệm của mỗi phương trình sau: 5 x 2 + 2 10 x + 2 3 = 0
Phương trình bậc hai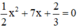 
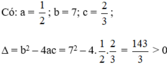
Vậy phương trình có hai nghiệm phân biệt.
Đúng 0
Bình luận (0)
Không giải phương trình, hãy xác định các hệ số a, b, c, tính biệt thức Δ và xác định số nghiệm của mỗi phương trình sau: 1 , 7 x 2 - 1 , 2 x - 2 , 1 = 0
Phương trình bậc hai 1,7x2 – 1,2x – 2,1 = 0
Có: a = 1,7; b = -1,2; c = -2,1; Δ = b2 – 4ac = (-1,2)2 – 4.1,7.(-2,1) = 15,72 > 0
Vậy phương trình có hai nghiệm phân biệt.
Đúng 0
Bình luận (0)
xác định hệ số a,b,c biết: (2x-5)(3a+b)=ax^2+x+c
Xác định hệ số a,b,c biết : (2x-5) . (3x+b) = ax^2+x+c
\( \left(2x-5\right)\left(3x+b\right)=ax^2+x+c\)
\(\Rightarrow2x\left(3x+b\right)-5\left(3x+b\right)=ax^2+x+c\)
\(\Rightarrow6x^2+2bx-15x-5b=ax^2+x+c\)
\(\)\(\Rightarrow6x^2+\left(2b-15\right)x-5b=ax^2+x+c\)
\(\Rightarrow\hept{\begin{cases}6x^2=ax^2\\\left(2b-15\right)x=x\\-5b=c\end{cases}\Rightarrow\hept{\begin{cases}a=6\\2b-15=1\\-5b=c\end{cases}\Rightarrow}}\hept{\begin{cases}a=6\\b=8\\c=-40\end{cases}}\)
Đúng 0
Bình luận (0)
a) Biết đồ thị hàm số y = ax + 7 đi qua M(2; 11). Xác định hệ số a?
b) Biết rằng khi x = 3 thì hàm số y = 2x + b có giá trị bằng 8. Xác định hệ số b?
SGK Chân trời sáng tạo trang 56
24 tháng 9 2023 lúc 22:49
Cho hàm số bậc hai \(y = f(x) = a{x^2} + bx + c\) có \(f(0) = 1,f(1) = 2,f(2) = 5.\)
a) Hãy xác định giá trị của các hệ số \(a,b\) và \(c.\)
b) Xác định tập giá trị và khoảng biến thiên của hàm số.
Tham khảo:
a) Ta có: \(f(0) = a{.0^2} + b.0 + c = 1 \Rightarrow c = 1.\)
Lại có:
\(f(1) = a{.1^2} + b.1 + c = 2 \Rightarrow a + b + 1 = 2\)
\(f(2) = a{.2^2} + b.2 + c = 5 \Rightarrow 4a + 2b + 1 = 5\)
Từ đó ta có hệ phương trình \(\left\{ \begin{array}{l}a + b + 1 = 2\\4a + 2b + 1 = 5\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}a + b = 1\\4a + 2b = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b = 0\end{array} \right.\)(thỏa mãn điều kiện \(a \ne 0\))
Vậy hàm số bậc hai đó là \(y = f(x) = {x^2} + 1\)
b) Tập giá trị \(T = \{ {x^2} + 1|x \in \mathbb{R}\} \)
Vì \({x^2} + 1 \ge 1\;\forall x \in \mathbb{R}\) nên \(T = [1; + \infty )\)
Đỉnh S có tọa độ: \({x_S} = \frac{{ - b}}{{2a}} = \frac{{ - 0}}{{2.1}} = 0;{y_S} = f(0) = 1\)
Hay \(S\left( {0;1} \right).\)
Vì hàm số bậc hai có \(a = 1 > 0\) nên ta có bảng biến thiên sau:
Hàm số nghịch biến trên khoảng \(\left( { - \infty ;0} \right)\) và đồng biến trên khoảng \(\left( {0; + \infty } \right)\)
Đúng 0
Bình luận (0)