Tìm 3 giá trị của y, sao cho:
3,5 < y < 3,51
Phải có lí do và lời giải thích
Gọi x và y là các số nguyên sao cho \(\left|x+y\right|>\left|1+xy\right|\). Tìm tất cả các giá trị của xy, và giải thích tại sao chúng là giá trị duy nhất có thể tìm được.
Cho bài toán: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = 2 x 4 − 4 x 2 + 3 . Dưới đây là lời giải của học sinh:
* Bước 1: Tập xác định D=R. Đạo hàm y ' = 8 x 3 − 8 x .
* Bước 2: Cho y ' = 0 tìm .
* Bước 3: Tính y 0 = 3 ; y − 1 = y 1 = 1 . Vậy giá trị lớn nhất của hàm số là 3, và giá trị nhỏ nhất là 1.
Lời giải trên đúng hay sai? Nếu sai thì giải sai từ bước mấy?
A. Bước 2.
B. Lời giải đúng.
C. Bước 3.
D. Bước 1.
Cho bài toán : Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = 2 x 4 − 4 x 2 + 3
Dưới đây là lời giải của một học sinh.
Bước 1: Tập xác định D = ℝ . y ' = 8 x 3 − 8 x
Bước 2. Cho y' = 0 tìm x = 0 ; x = − 1 ; x = 1
Bước 3. Tính được y 0 = 3 ; y − 1 = 1 ; y 1 = 1. Vậy giá trị lớn nhất của hàm số là 3 , và giá trị nhỏ nhất là 1. Lời giải trên đúng hay sai? Nếu sai thì lời giải sai từ bước mấy?
A. Bước 2.
B. Lời giải đúng.
C. Bước 3.
D. Bước 1.
Đáp án C
Lưu ý: Đề không cho tìm max – min trên đoạn nên ta không thể so sánh các giá trị như vậy
Cách giải: Lập BBT và ở đây kết luận được giá trị nhỏ nhất của hàm số là 1 , nhưng hàm số không có giá trị lớn nhất.
Cho bài toán: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = 2 x 4 − 4 x 2 + 3 . Dưới đây là lời giải của học sinh:
* Bước 1: Tập xác định D = ℝ . Đạo hàm y ' = 8 x 3 − 8 x .
* Bước 2: Cho y ' = 0 tìm x = 0 ; x = − 1 ; x = 1 .
* Bước 3: Tính y 0 = 3 ; y − 1 = y 1 = 1 . Vậy giá trị lớn nhất của hàm số là 3, và giá trị nhỏ nhất là 1.
Lời giải trên đúng hay sai? Nếu sai thì giải sai từ bước mấy?
A. Bước 2
B. Lời giải đúng
C. Bước 3
D. Bước 1
Đáp án C
Lời giải trên là sai. Cách làm lời giải này chỉ đúng đối với bài toán tìm giá trị lớn nhất – giá trị nhỏ nhất của hàm số trên một đoạn .
Để giải bài toán này, ta lập bảng biến thiên của hàm số y = 2 x 4 − 4 x 2 + 3 trên R
* Bước 1: Tập xác định D = ℝ . Đạo hàm y ' = 8 x 3 − 8 x .
* Bước 2: Cho y ' = 0 tìm x = 0 ; x = − 1 ; x = 1 .
* Bước 3: Ta có bảng biến thiên sau:
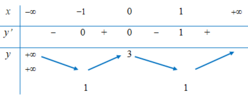
Quan sát bảng biến thiên, ta thấy giá trị nhỏ nhất của hàm số là 1 và hàm số không có giá trị lớn nhất. Vậy lời giải trên sai từ bước 3.
Cho ba đường thẳng sau:
y = 2/5x + 1/2 ( d 1 ) ;
y = 3/5x - 5/2 ( d 2 ) ;
y = kx + 3,5 ( d 3 )
Hãy tìm giá trị của k để sao cho ba đường thẳng đồng quy tại một điểm.
* Trước hết tìm giao điểm của hai đường thẳng ( d 1 ) và ( d 2 ).
- Tìm hoành độ của giao điểm:
2/5x + 1/2 = 3/5x - 5/2 ⇔ 1/5x = 6/2 ⇔ x = 15.
- Tìm tung độ giao điểm:
y = 2/5.15 + 1/2 = 6,5.
*Tìm k (bằng cách thay tọa độ của giao điểm vào phương trình ( d 3 ).
6,5 = k.15 + 3,5 ⇔ 15k = 3 ⇔ k = 0,2.
Trả lời: Khi k = 0,2 thì ba đường thẳng đồng quy tại điểm (15; 6,5).
Tìm giá trị của y sao cho
Biểu thức (y-1)/(y-2) - (3+y)/(y-4) và biểu thức -2/(y-2)(y-4) có giá trị bằng nhau
\(ĐKXĐ:\hept{\begin{cases}y\ne2\\y\ne4\end{cases}}\)
\(\frac{y-1}{y-2}-\frac{3+y}{y-4}=\frac{-2}{\left(y-2\right)\left(y-4\right)}\)
\(\Leftrightarrow\frac{\left(y-1\right)\left(y-4\right)-\left(3+y\right)\left(y-2\right)}{\left(y-2\right)\left(y-4\right)}=\frac{-2}{\left(y-2\right)\left(y-4\right)}\)
\(\Leftrightarrow y^2-5y+4-y^2-y+6=-2\)
\(\Leftrightarrow-6y+10=-2\)
\(\Leftrightarrow-6y+12=0\)
\(\Leftrightarrow y=2\)(KTM)
Vậy tập nghiệm của phương trình là \(S=\varnothing\)
Cho A={-14;21;-23;34;19;0}.Tìm x,y thuộc A,x và y khác nhau sao cho
a) Tổng x+y đật giá trị lớn nhất
b) Tổng x+y đạt giá trị nhỏ nhất
Giúp mình với mình sẽ cho think nhưng trả lời đầy đủ nha đừng có trả lời mỗi đáp thôi.Thanks mọi người ạ !!!!!!!
Tìm giá trị lớn nhất của:
A = 0,5 - | x - 3,5|
B = - | 1,4 - x | - 2
Tìm giá trị nhỏ nhất:
c = 1,7 + | 3,4 - x |
D = | x + 2,8 | -3,5
Ai trả lời đúng lời giải rõ ràng chi tiết tớ tik cho 6 cái ko nói điêu ~~
a) |x-3,5| \(\ge\)0.
Vậy 0,5 - |x-3,5| \(\le\)0,5.
Vậy GTLN cùa A bằng 0,5 tại x-3,5 = 0 hay x = 3,5.
b) -|1,4-x| \(\le\)0.
Vậy -|1,4-x| - 2 \(\le\)-2.
Vậy GTLN của B bằng -2 tại 1,4 - x = 0 hay x = 1,4.
c) |3,4-x| \(\ge\)0.
Vậy 1,7 + |3,4-x| \(\ge\)1,7.
Vậy GTNN của C bằng 1,7 tại 3,4 - x = 0 hay x = 3,4.
d) |x+2,8| \(\ge\)0.
Vậy |x+2,8| - 3,5 \(\ge\)3,5.
Vậy GTNN của D bằng 3,5 tại x + 2,8 = 0 hay x = -2,8.
a)Ta thấy:- | x - 3,5|=<0
=> 0-5-| x - 3,5|=<0,5-0=0,5
=> A=<0,5
Dấu = khi x=3,5
Vậy...
Ta thấy:-|1,4-x|=<0
=>-|1,4-x|-2=<0-2=-2
=>B=<-2
Dấu = khi x=1,4
Vậy...
b)Ta thấy:|3,4-x|>=0
=>1,7+|3,4-x|>=1,7+0=1,7
=>C>=1,7
Dấu = khi x=3,4
Vậy....
Ta thấy:|x+2,8|>=0
=>|x+2,8|-3,5>=0-3,5=-3,5
=>D>=-3,5
Dấu = khi x=-2,8
Vậy....
+Để A max thì /x-3,5/ min
mà /x-3,5/ > hoặc = 0 nên /x-3,5/ min=0
=> A max=0,5-0=0,5
+Để B max thì -/1,4-x/ max
mà -/1,4-x/ < hoặc = 0 nên -/1,4-x/ max=0
=>B max =0-2= -2
+Để C min thì /3,4-x/ min
mà /3,4-x/ > hoặc = 0 nên /3,4-x/ min =0
=>C min=1,7+0+1,7
+Để D min thì /x+2,8/ min
mà /x+2,8/ > hoặc = 0 nên /x+2,8/ min =0
=>D=0-3,5= -3,5
tìm x và y bt:X+10/5=6/Y+1
tìm số nguyên n để 2n+3/n là một số nguyên
tìm số nguyên tố n để n+3 là số nguyên tố
Cho số tự nhiên n.Hãy giải thích tại sao 2n+3/2n+5 tối giản với các giá trị của n
b: Để A nguyên thì 2n+3 chia hết cho n
=>3 chia hết cho n
=>n thuộc {1;-1;3;-3}
c: Th1: n=2
=>n+3=5(nhận)
TH2: n=2k+1
=>n+3=2k+4=2(k+2)
=>Loại
d: Gọi d=ƯCLN(2n+3;2n+5)
=>2n+5-2n-3 chia hết cho d
=>2 chia hết cho d
mà 2n+3 lẻ
nên d=1
=>PSTG