giải các phương trình sau
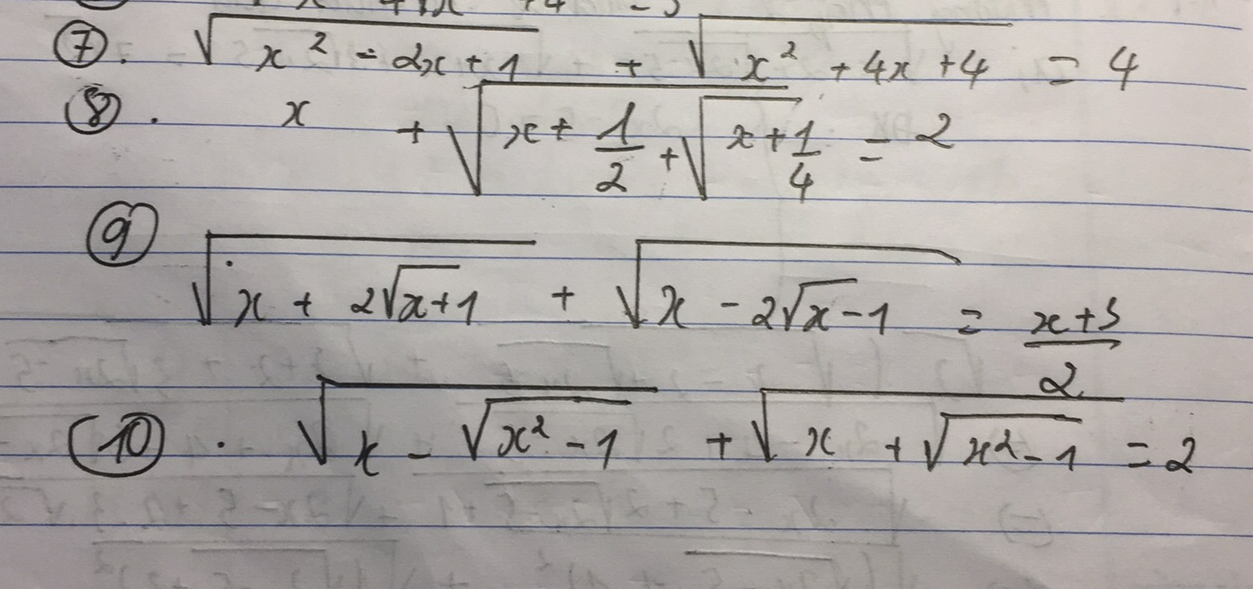
nhờ các bạn và thầy cô giải giúp mình , mình cảm ơn
Giải hệ phương trình :

Mình đang cần gấp ạ ! Các bạn giải giúp mình ! Mình cảm ơn !
22.
ĐKXĐ: \(y\ne1\)
\(\left\{{}\begin{matrix}x^2-\dfrac{1}{y-1}=2\\2x^2+\dfrac{3}{1-y}=2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x^2+\dfrac{2}{1-y}=4\\2x^2+\dfrac{3}{1-y}=2\end{matrix}\right.\)
Trừ pt dưới cho trên:
\(\Rightarrow\dfrac{1}{1-y}=-2\)
\(\Rightarrow1-y=-\dfrac{1}{2}\Rightarrow y=\dfrac{3}{2}\)
Thế vào \(x^2-\dfrac{1}{y-1}=2\)
\(\Rightarrow x^2=4\Rightarrow x=\pm2\)
Vậy nghiệm của hệ là \(\left(x;y\right)=\left(2;\dfrac{3}{2}\right);\left(-2;\dfrac{3}{2}\right)\)
b.
ĐKXĐ: \(x\ne-\dfrac{1}{2}\)
\(Hệ\Leftrightarrow\left\{{}\begin{matrix}2y^2-\dfrac{10}{2x+1}=8\\2y^2-\dfrac{11}{2x+1}=7\end{matrix}\right.\)
Trừ pt trên cho dưới:
\(\Rightarrow\dfrac{1}{2x+1}=1\)
\(\Rightarrow2x+1=1\)
\(\Rightarrow x=0\)
Thế vào \(y^2-\dfrac{5}{2x+1}=4\)
\(\Rightarrow y^2=9\Rightarrow y=\pm3\)
Vậy nghiệm của hệ là \(\left(x;y\right)=\left(0;3\right);\left(0;-3\right)\)
1 phần 20 là bao nhiêu yến?
Trả lời sớm gúp mình và giải thích được không ạ?
Cảm ơn các bạn,các anh chị,các thầy cô đã chỉ cho mình^^
ở chỗ 1 phần 20 ko có đơn vị rồi
Mình có bài này không biết giải,nhờ các bạn giải giùm mình nha!
Đề bài như sau:
abcde x 9 = edcba.
Nhờ các bạn giải hộ nha
Các bạn làm lời giải ở dưới,và làm bài giải đàng hoảng cho mình với nha,cảm ơn nhiều!
Cảm ơn bạn nhiều,nhưng bạn có thể giải giúp mình được không?
đặt cột dọc là được cậu ơi để tớ viết lời giải ở dưới nha
Cho 60 số tự nhiên liên tiếp,lấy ra ít nhất bao nhiêu số tự nhiên bất kì trong chúng để có tổng hai số tự nhiên liên tiếp:
a) chia hết cho 2
b)chia hết cho 3
Mình nhờ cậu và các cô,thầy giáo trong ban quản lý giúp với ạ.em đang cần gấp mà hỏi mấy cô chuyên toán cũng không giải được.Mình mong chờ vào các bạn,các thầy cô giáo cả.Nhờ mọi người trình bày bài và có lập luận để đưa ra bài đúng luôn nha1Xin cảm ơn mọi người rất nhiều!
Nhờ thầy cô và các bạn giúp em ạ. Em cảm ơn.
14.
\(\left(ab+c\right)\left(bc+a\right)\le\dfrac{1}{4}\left(ab+bc+c+a\right)^2=\dfrac{1}{4}\left(a+c\right)^2\left(b+1\right)^2\)
Tương tự:
\(\left(ab+c\right)\left(ca+b\right)\le\dfrac{1}{4}\left(b+c\right)^2\left(a+1\right)^2\)
\(\left(bc+a\right)\left(ca+b\right)\le\dfrac{1}{4}\left(a+b\right)^2\left(c+1\right)^2\)
Nhân vế với vế và khai căn:
\(\left(ab+c\right)\left(bc+a\right)\left(ca+b\right)\le\dfrac{1}{8}\left(a+b\right)\left(b+c\right)\left(c+a\right)\left(a+1\right)\left(b+1\right)\left(c+1\right)\)
Mặt khác ta có:
\(\left(a+1\right)\left(b+1\right)\left(c+1\right)\le\dfrac{1}{27}\left(a+b+c+3\right)^3=8\)
\(\Rightarrow\left(ab+c\right)\left(bc+a\right)\left(ca+b\right)\le\dfrac{1}{8}.8.\left(a+b\right)\left(b+c\right)\left(c+a\right)\)
Dấu "=" xảy ra khi...
15.
\(\Leftrightarrow\sum\dfrac{2a^2}{2a^2+\left(b+c-a\right)^2}\le2\)
\(\Leftrightarrow\sum\left(\dfrac{2a^2}{2a^2+\left(b+c-a\right)^2}-1\right)\le2-3\)
\(\Leftrightarrow\sum\dfrac{\left(b+c-a\right)^2}{2a^2+\left(b+c-a\right)^2}\ge1\)
Đặt \(\left\{{}\begin{matrix}b+c-a=x\\c+a-b=y\\a+b-c=z\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=\dfrac{y+z}{2}\\b=\dfrac{x+z}{2}\\c=\dfrac{x+y}{2}\end{matrix}\right.\)
\(VT=\sum\dfrac{x^2}{2\left(\dfrac{y+z}{2}\right)^2+x^2}=\sum\dfrac{2x^2}{2x^2+\left(y+z\right)^2}\ge\sum\dfrac{2x^2}{2x^2+2\left(y^2+z^2\right)}=1\)
Dấu "=" xảy ra khi...
Các bạn ơi giải giúp mình với
Giải phương trình sau:
4+2x(2x+4) = -x
Cảm ơn mn nha
\(4+2x\left(2x+4\right)=-x\)
\(4+4x^2+8x=-x\)
\(4+4x^2+8x+x=0\)
\(4+4x^2+9x=0\)
=> vô nghiệm
các bạn giúp mình câu này với
giải phương trình sau: \(\dfrac{x+2}{x-2}\)-\(\dfrac{2}{x^2-2x}\)=\(\dfrac{1}{x}\)
mình cảm ơn nhiều ạ.
\(\dfrac{x+2}{x-2}-\dfrac{2}{x^2-2x}=\dfrac{1}{x}\left(đk:x\ne0,x\ne2\right)\)
\(\Leftrightarrow\dfrac{\left(x+2\right)x-2}{x\left(x-2\right)}=\dfrac{x^2-2x}{x\left(x-2\right)}\)
\(\Leftrightarrow x^2+2x-2=x^2-2x\)
\(\Leftrightarrow4x=2\Leftrightarrow x=\dfrac{1}{2}\)
Cho mình sửa lại nhé:
\(\dfrac{x+2}{x-2}-\dfrac{2}{x^2-2x}=\dfrac{1}{x}\left(đk:x\ne0,x\ne2\right)\)
\(\Leftrightarrow\dfrac{\left(x+2\right)x-2}{x\left(x-2\right)}=\dfrac{x-2}{x\left(x-2\right)}\)
\(\Leftrightarrow x^2+2x-2=x-2\)
\(\Leftrightarrow x^2+x=0\)
\(\Leftrightarrow x\left(x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\left(ktm\right)\\x=-1\left(tm\right)\end{matrix}\right.\)
Nhờ thầy cô và các bạn giúp em câu 1.1.16 và 1.1.17 ạ. Em cảm ơn.
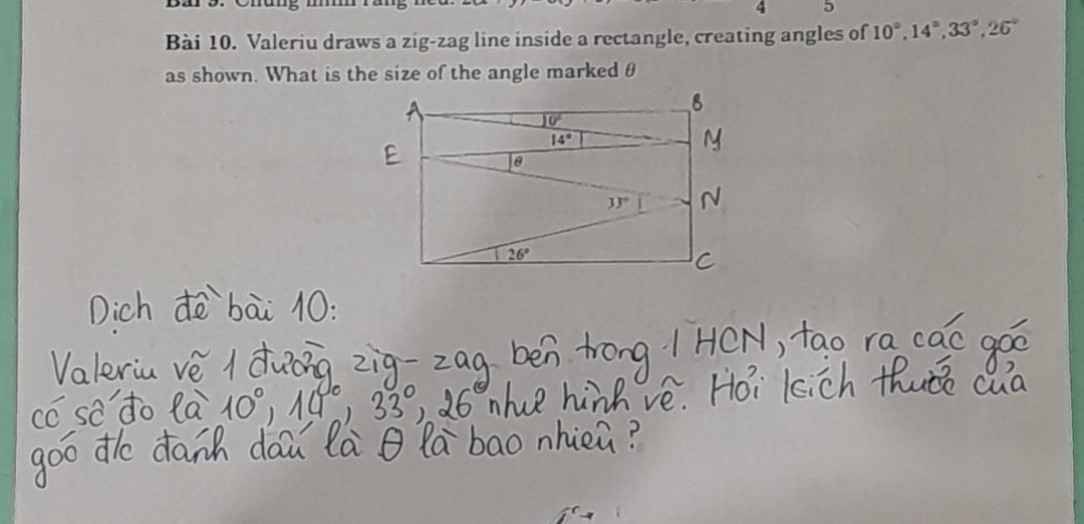 Nhờ các bạn giải giúp mình 2 bài này nha cảm ơn csc bạn nhiều!!!!
Nhờ các bạn giải giúp mình 2 bài này nha cảm ơn csc bạn nhiều!!!!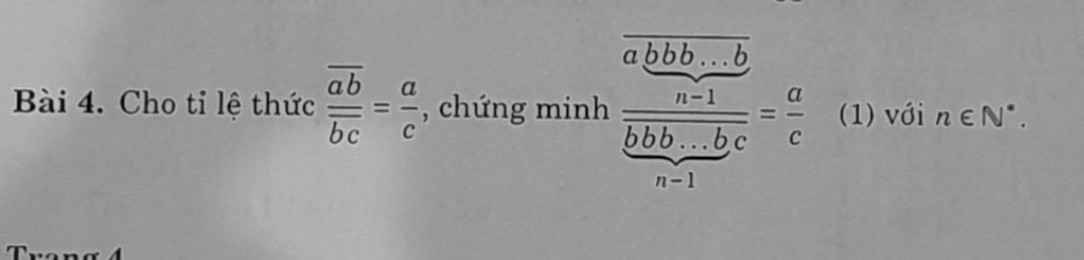
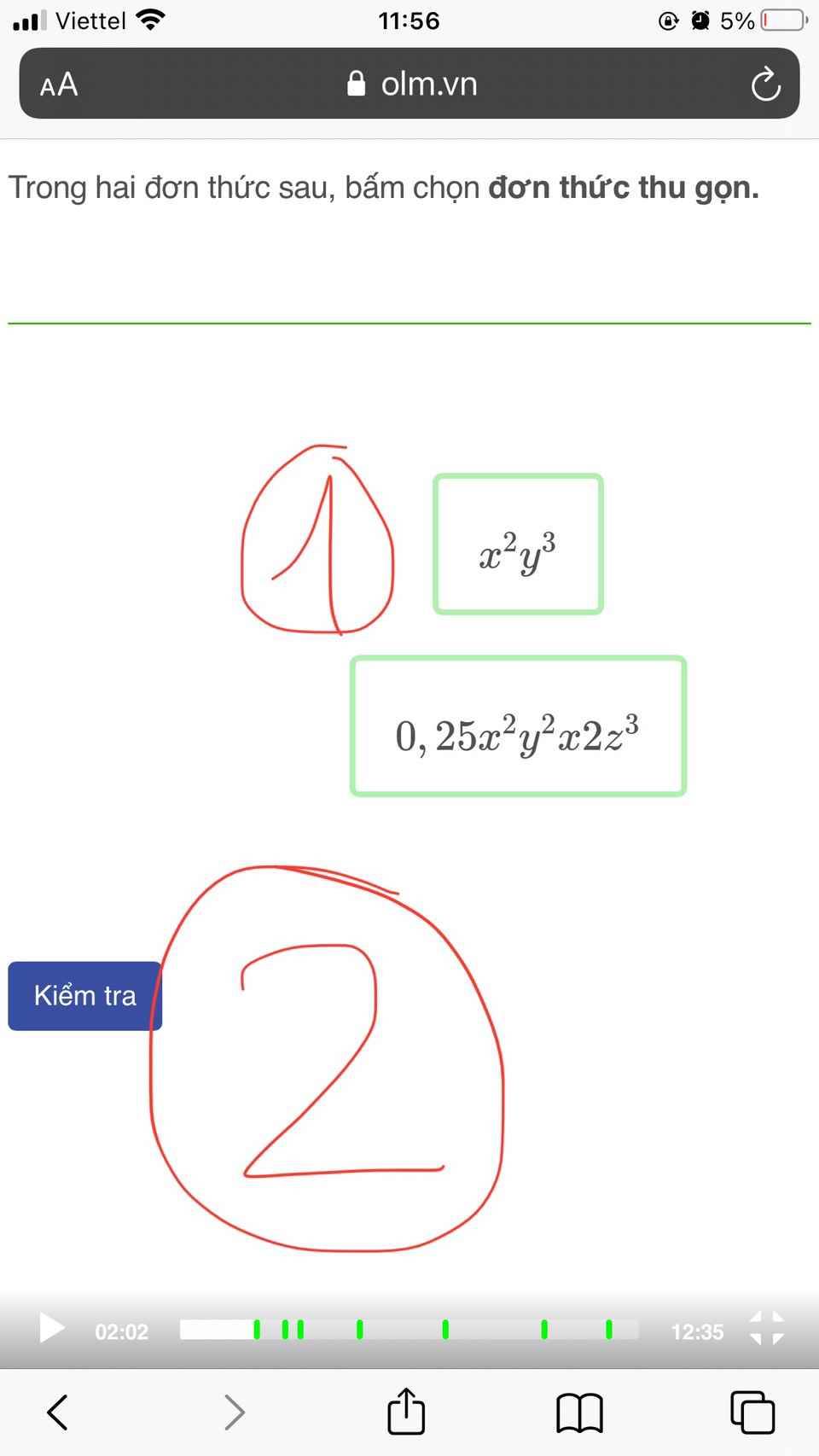
Mình chưa biết code như thế nào để chọn đáp án
Nhờ các thầy cô chỉ giúp. Xin cảm ơn!
Chào em, cảm ơn em đã tham gia nền tảng học trực tuyến olm.vn. Với những bài thực hành như này Olm xin hướng dẫn em làm như sau: Bước 1 em chọn đáp án đúng. Bước 2 em bấm kiểm tra vậy là ok rồi em nhá.