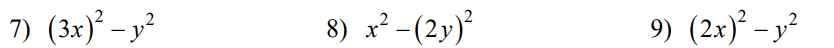
\(7)\)  \(\left(3x\right)^2-y^2=\left(3x-y\right)\left(3x+y\right)\)

\(8)\)  \(x^2-\left(2y\right)^2=\left(x-2y\right)\left(x+2y\right)\)

\(9)\)  \(\left(2x\right)^2-y^2=\left(2x-y\right)\left(2x+y\right)\)

\(\left(x-6\right)\left(6+x\right)=\left(x-6\right)\left(x+6\right)=x^2-6^2=x^2-36\)

=(x-6) (x+6= \(x^2-6^2=x^2-36\)

( A   –   B ) 3   =   ( A   +   ( - B ) ) 3       =   A 3   +   3 . A 2 . ( - B )   +   3 . A . ( - B ) 2   +   ( - B ) 3       =   A 3   –   3 A 2 B   +   3 A B 2   –   B 3     = >   ( A   –   B ) 3   =   A 3   –   3 A 2 B   –   3 A B 2   +   B 3

là sai

Đáp án cần chọn là: B

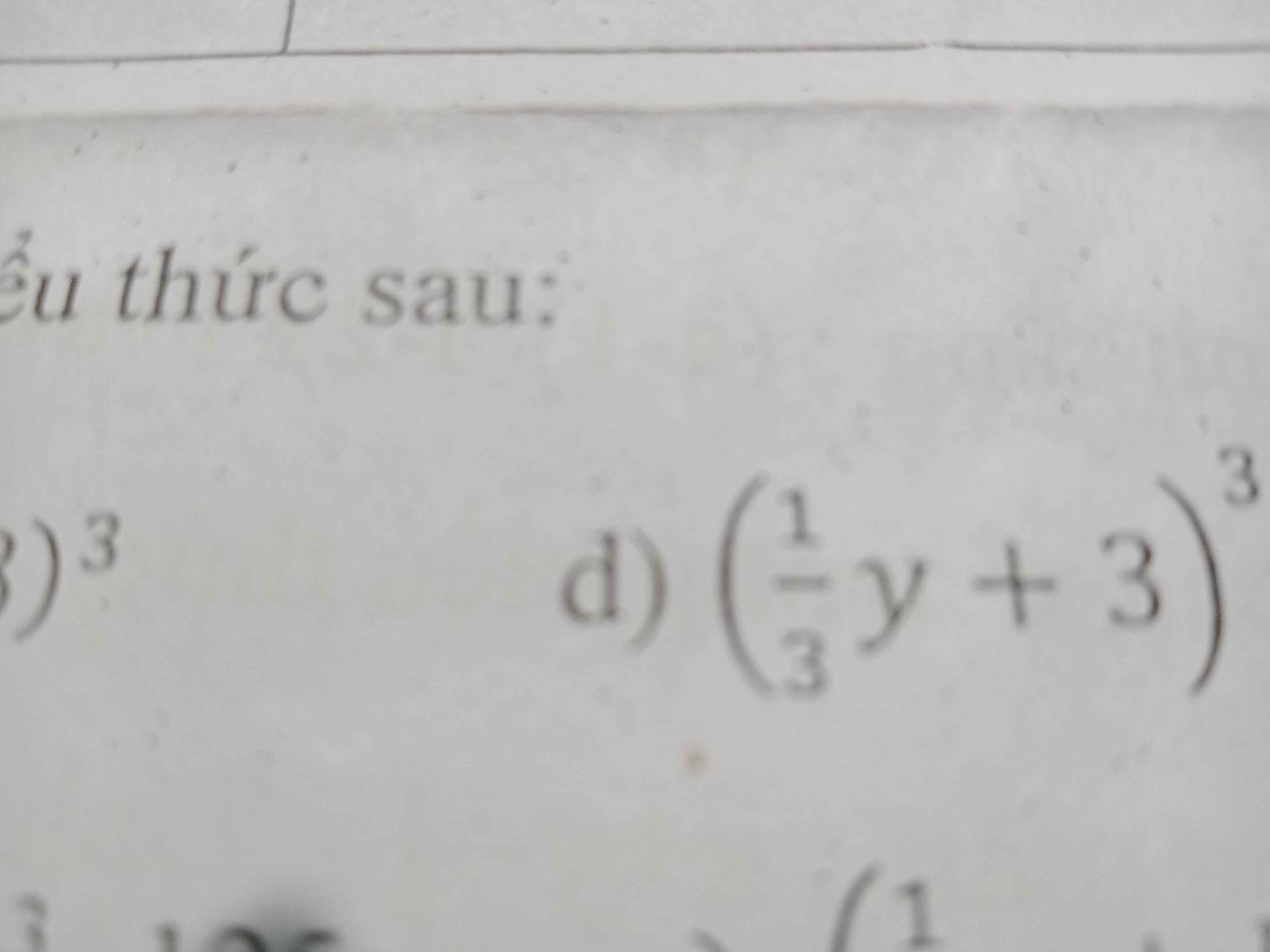
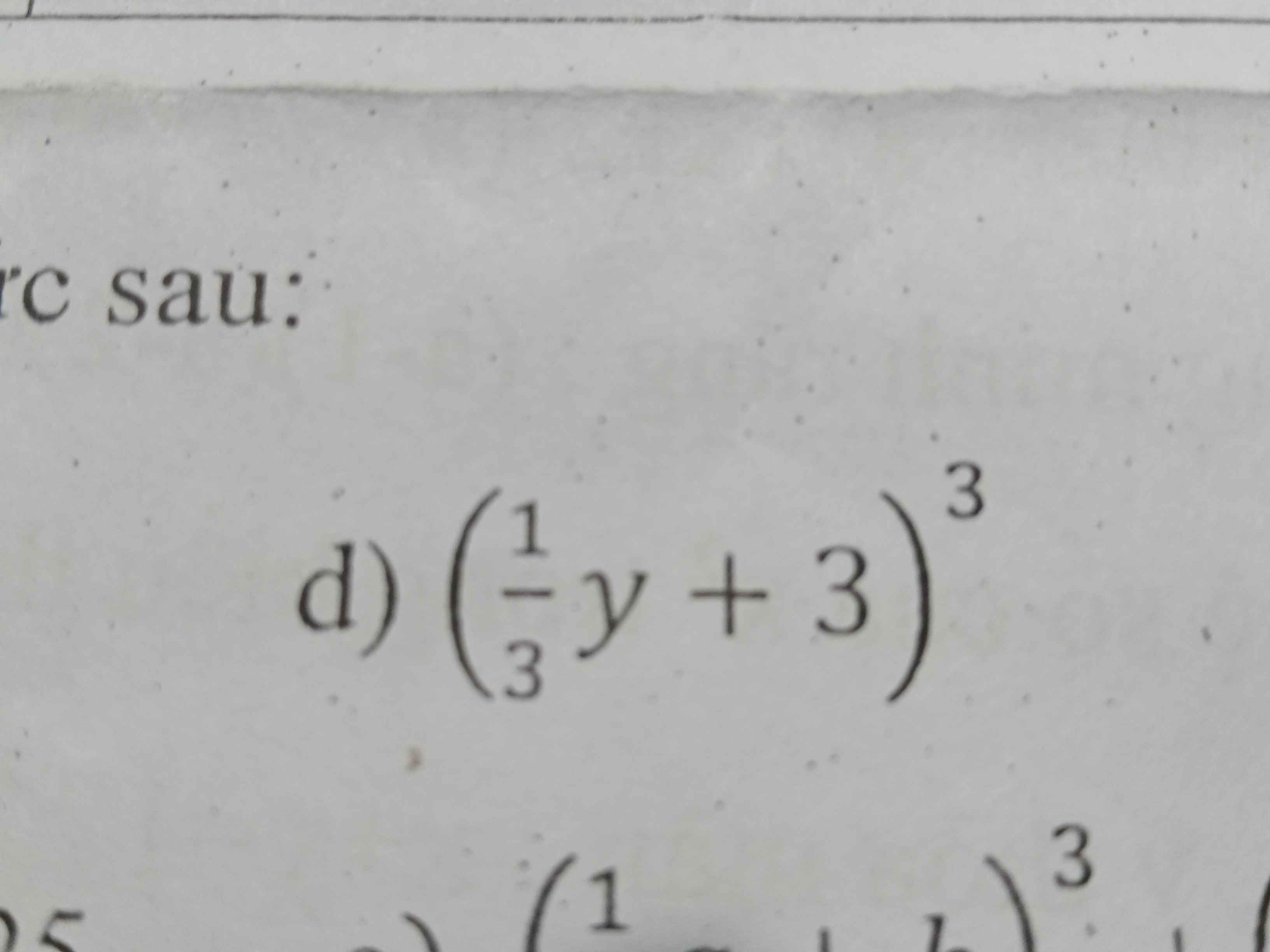
(1𝑦/3+3)^3

(𝑦/3+3)^3

(𝑦/3+3⋅3/3)^3

(𝑦+3⋅3/3)^3

(𝑦+9/3)^3

\(\left(\dfrac{1}{3}y+3\right)^3=\dfrac{1}{27}y^3+y^2+9y+27\)

Ta có:(a²+ab+b²)(a²-ab+b²)-(a⁴+b⁴)

    =   (a²+b²)²-a²b²-a⁴-b⁴=a⁴+2a²b²+b⁴-a²b²-a⁴-b⁴=a²b²

Ta có:(a²+ab+b²)(a²-ab+b²)-(a⁴+b⁴)

    =   (a²+b²)²-a²b²-a⁴-b⁴=a⁴+2a²b²+b⁴-a²b²-a⁴-b⁴=a²b²

\(\left(\dfrac{1}{3y+3}\right)^3=\dfrac{1}{\left(3y+3\right)^3}=\dfrac{1}{27y^3+81y^2+81y+27}\)

\(\left(\dfrac{1}{3y+3}\right)^3=\dfrac{1^3}{\left(3y+3\right)^3}=\dfrac{1}{27\left(y^3+3y^2+3y+1\right)}\)

\(\left(\dfrac{1}{3}y+3\right)^3=\dfrac{1}{27}y^3+y^2+9y+27\)

\(=x^3+9x^2+27x+27\)

a: Ta có: \(\left(x+y\right)^3-\left(x-y\right)^3\)

\(=x^3+3x^2y+3xy^2+y^3-x^3+3x^2y-3xy^2+y^3\)

\(=6x^2y+2y^3\)

\(\left(x+y\right)^3-\left(x-y\right)^3\)

\(=\left(x+y-x+y\right)^3+3\left(x+y\right)\left(x-y\right)\left(x+y-x+y\right)\)

\(=8y^3+6y\left(x^2-y^2\right)\)

\(=8y^3+6x^2y-6y^3\)

\(=2y^3+6x^2y\)

\(=\left[\left(2x^2+1\right)^2-\left(2x\right)^2\right]-\left(2x^2+1\right)^2=-4x^2\)

Bài 1: 

c: \(\left(-5x-y\right)^3=-125x^3-75x^2y-15xy^2-y^3\)

h: \(\left(3y-2x^2\right)^3=27y^3-54y^2x^2+36yx^4-8x^6\)

Bài 1:

c. (-5x - y)³ = -125x³ - 50x²y - 10xy² - y³

d. (3y - 2x²)³ = 27y³ - 18x²y² + 24xy⁴ - 8x⁶