Câu 2 pls

Những câu hỏi liên quan
Pls giải câu b bài 2
Lời giải:
Theo định lý Viet:
$x_1+x_2=\frac{2}{2}=1$
$x_1x_2=\frac{-1}{2}$
Ta có:
$y_1+y_2=\frac{1}{x_1-1}+\frac{1}{x_2-1}=\frac{x_1+x_2-2}{(x_1-1)(x_2-1)}$
$=\frac{x_1+x_2-2}{x_1x_2-(x_1+x_2)+1}=\frac{1-2}{\frac{-1}{2}-1+1}=2$
$y_1y_2=\frac{1}{x_1-1}.\frac{1}{x_2-1}=\frac{1}{x_1x_2-(x_1+x_2)+1}$
$=\frac{1}{\frac{-1}{2}-1+1}=-2$
Theo định lý Viet đảo, $y_1,y_2$ là nghiệm của pt:
$y^2-2y-2=0$
Đúng 1
Bình luận (2)
Lời giải:
Theo định lý Viet:
$x_1+x_2=\frac{2}{2}=1$
$x_1x_2=\frac{-1}{2}$
Ta có:
$y_1+y_2=\frac{1}{x_1-1}+\frac{1}{x_2-1}=\frac{x_1+x_2-2}{(x_1-1)(x_2-1)}$
$=\frac{x_1+x_2-2}{x_1x_2-(x_1+x_2)+1}=\frac{1-2}{\frac{-1}{2}-1+1}=2$
$y_1y_2=\frac{1}{x_1-1}.\frac{1}{x_2-1}=\frac{1}{x_1x_2-(x_1+x_2)+1}$
$=\frac{1}{\frac{-1}{2}-1+1}=-2$
Theo định lý Viet đảo, $y_1,y_2$ là nghiệm của pt:
$y^2-2y-2=0$
ai làm hộ em 2 câu này với pls
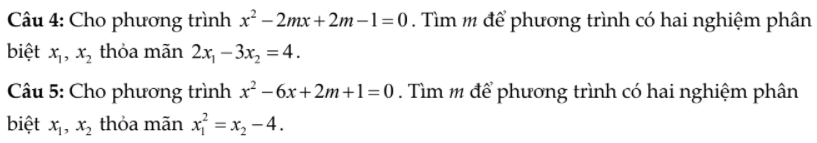
Bài 2 :
\(\Delta'=m^2-\left(2m-1\right)=\left(m-1\right)^2\ge0\)
Để pt có 2 nghiệm pb
\(m-1\ne0\Leftrightarrow m\ne1\)
Theo Vi et \(\left\{{}\begin{matrix}x_1+x_2=2m\left(1\right)\\x_1x_2=2m-1\left(2\right)\end{matrix}\right.\)
Ta có : \(2x_1-3x_2=4\left(3\right)\)
Từ (1) ; (3) ta có hệ \(\left\{{}\begin{matrix}x_1+x_2=2m\\2x_1-3x_2=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x_1+2x_2=4m\\2x_1-3x_2=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5x_2=4m-4\\x_1=2m-x_2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_2=\dfrac{4m-4}{5}\\x_1=2m-\dfrac{4m-4}{5}=\dfrac{6m+4}{5}\end{matrix}\right.\)
Thay vào (3) ta được \(\left(\dfrac{6m+4}{5}\right)\left(\dfrac{4m+4}{5}\right)=2m-1\)
\(\Rightarrow\left(6m+4\right)\left(4m+4\right)=50m-25\Leftrightarrow24m^2+40m+16=50m-25\)
\(\Leftrightarrow24m^2-10m+41=0\)
\(\Delta'=10-41.24< 0\)Vậy pt vô nghiệm hay ko có gtri m
Đúng 1
Bình luận (0)
5.
\(\Delta'=9-\left(2m+1\right)=8-2m>0\Rightarrow m< 4\)
Theo Viet: \(\left\{{}\begin{matrix}x_1+x_2=6\\x_1x_2=2m+1\end{matrix}\right.\)
Kết hợp Viet và điều kiện đề bài:
\(\left\{{}\begin{matrix}x_1+x_2=6\\x_1^2=x_2-4\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x_2=6-x_1\\x_1^2=6-x_1-4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_2=6-x_1\\x_1^2+x_1-2=0\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x_1=1;x_2=5\\x_1=-2;x_2=8\end{matrix}\right.\)
Thế vào \(x_1x_2=2m+1\Rightarrow\left[{}\begin{matrix}2m+1=5\\2m+1=-16\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}m=2\\m=-\dfrac{17}{2}\end{matrix}\right.\) (thỏa mãn)
Đúng 1
Bình luận (0)
help pls ~![]() câu b bài 2 là 3/8 nha
câu b bài 2 là 3/8 nha 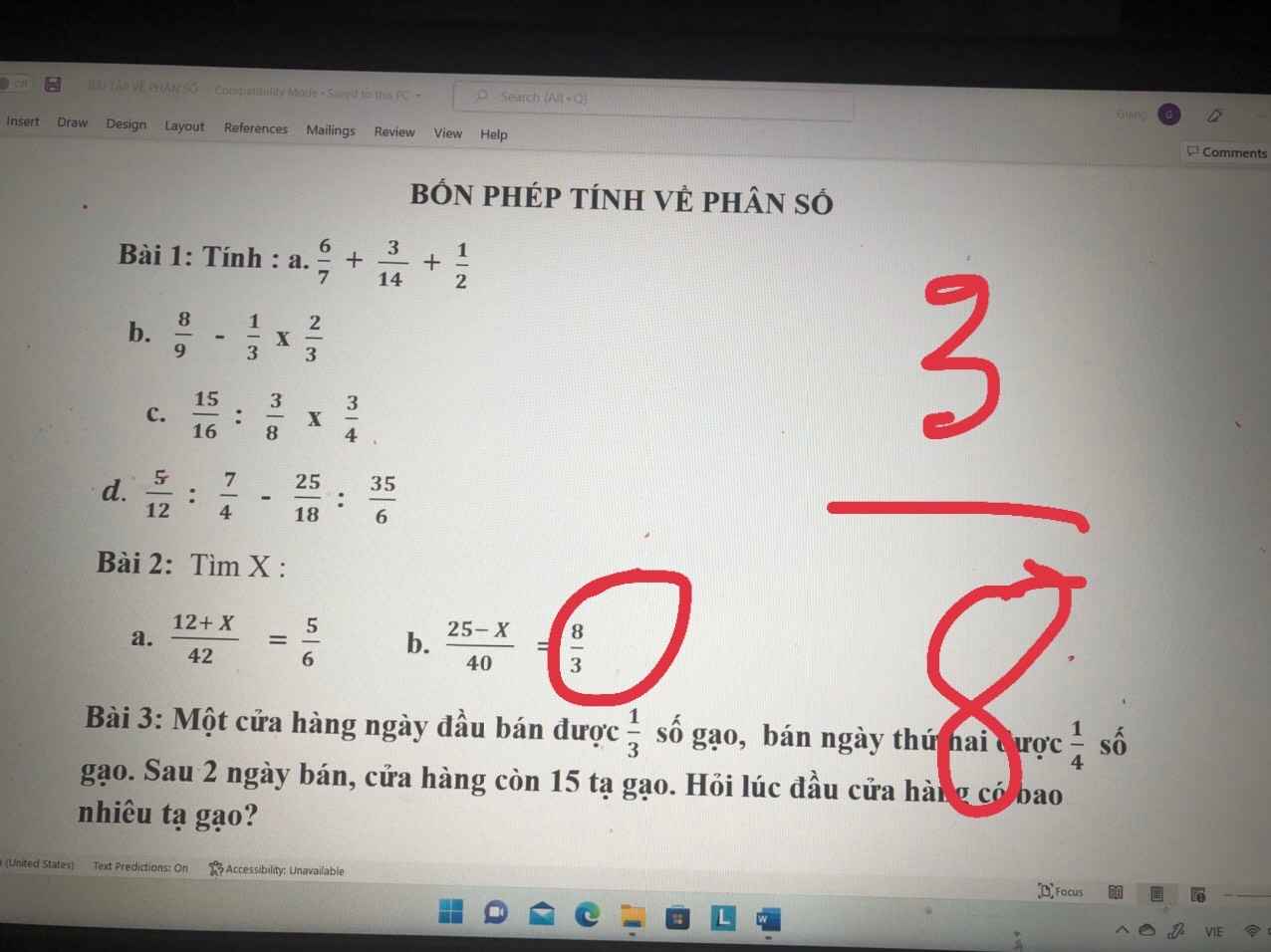
25-x/40=3/8
25-x/40=15/40
khử mẫu:25-x=15
x=25-15
x=10
Đúng 1
Bình luận (2)
ai làm hộ em 2 câu hình này với pls

ai làm hộ 2 câu hình này với ạ pls

PLS HELp câu 3 
đặt 2 câu có từ sáo là từ đồng âm
help me pls
Con chim sáo đang đậu trên cành cây.
Chú thổi sáo này tài quá !
Mik làm theo yêu cầu đó
Con sáo đó hót rất hay
Mọi thứ bị sáo trộn hết cả rồi
cảm ơn rất nhiều
Xem thêm câu trả lời
Giúp em câu 1b và câu 4 với ạ ,pls!!!!

1.
b, \(B=\dfrac{8+2\sqrt{2}}{3-\sqrt{2}}-\dfrac{2+3\sqrt{2}}{\sqrt{2}}+\dfrac{\sqrt{2}}{1-\sqrt{2}}\)
\(=\dfrac{2\left(2+\sqrt{2}\right)\left(3-\sqrt{2}\right)}{3-\sqrt{2}}-\dfrac{\sqrt{2}\left(\sqrt{2}+3\right)}{\sqrt{2}}+\dfrac{\sqrt{2}\left(1+\sqrt{2}\right)}{1-\sqrt{2}}\)
\(=4+2\sqrt{2}-\sqrt{2}-3-2-\sqrt{2}\)
\(=-1\)
Đúng 1
Bình luận (0)
Bài 1:
b: Ta có: \(B=\dfrac{8+2\sqrt{2}}{3-\sqrt{2}}-\dfrac{2+3\sqrt{2}}{\sqrt{2}}-\dfrac{\sqrt{2}}{\sqrt{2}-1}\)
\(=2\sqrt{2}\left(\sqrt{2}+1\right)-\sqrt{2}-3-2+\sqrt{2}\)
\(=4+2\sqrt{2}-5\)
\(=2\sqrt{2}-1\)
Đúng 1
Bình luận (0)
4.
a, ĐK: \(x\ge0;x\ne1\)
\(Q=\left(\dfrac{\sqrt{x}-2}{x-1}-\dfrac{\sqrt{x}+2}{x+2\sqrt{x}+1}\right).\dfrac{\left(1-x\right)^2}{2}\)
\(=\left[\dfrac{\sqrt{x}-2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}-\dfrac{\sqrt{x}+2}{\left(\sqrt{x}+1\right)^2}\right].\dfrac{\left(1-x\right)^2}{2}\)
\(=\left[\dfrac{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)^2}-\dfrac{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)^2}\right].\dfrac{\left(1-x\right)^2}{2}\)
\(=\left[\dfrac{x-\sqrt{x}-2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)^2}-\dfrac{x+\sqrt{x}-2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)^2}\right].\dfrac{\left(1-x\right)^2}{2}\)
\(=\dfrac{2\sqrt{x}}{\left(1-x\right)\left(\sqrt{x}+1\right)}.\dfrac{\left(1-x\right)^2}{2}\)
\(=\dfrac{\sqrt{x}\left(1-\sqrt{x}\right)\left(\sqrt{x}+1\right)}{\sqrt{x}+1}\)
\(=\sqrt{x}-x\)
b, \(Q=\sqrt{x}-x=\sqrt{x}\left(1-\sqrt{x}\right)>0\)
\(\Leftrightarrow1-\sqrt{x}>0\)
\(\Leftrightarrow\sqrt{x}< 1\)
\(\Leftrightarrow x< 1\)
Vậy \(0\le x< 1\)
c, \(Q=\sqrt{x}-x\)
\(=-\left(x-\sqrt{x}+\dfrac{1}{4}\right)+\dfrac{1}{4}\)
\(=-\left(\sqrt{x}-\dfrac{1}{2}\right)^2+\dfrac{1}{4}\le\dfrac{1}{4}\)
\(\Rightarrow maxQ=\dfrac{1}{4}\Leftrightarrow x=\dfrac{1}{4}\)
Đúng 1
Bình luận (0)
Ai giúp mình câu này pls ;-;
\(n_{H_2}=\dfrac{3,36}{22,4}=0,15(mol)\\ PTHH:2Al+6HCl\to 2AlCl_3+3H_2\\ Al_2O_3+6HCl\to 2AlCl_3+3H_2O\\ \Rightarrow n_{Al}=\dfrac{2}{3}n_{H_2}=0,1(mol)\\ \Rightarrow m_{Al}=0,1.27=2,7(g)\\ \Rightarrow \%_{Al}=\dfrac{2,7}{5}.100\%=54\%\\ \Rightarrow \%_{Al_2O_3}=100\%-54\%=46\%\)
Đúng 2
Bình luận (0)
nH2=3,36/22,4=0,15
Đặt x,y lần lượt là số mol của al và al2o3
2Al+6Hcl----->2AlCl3+3H2
x 3/2x
Al2O3+6Hcl---->2AlCl3+3H2O
y
=>27x+102y=5(1)
3/2x=0,15(2)
Từ (1),(2)=>x=0,1,y=0,023
%Al=0,1*27/5*100%=54%
%Al2O3=100%-54%=46%
Đúng 0
Bình luận (0)
nH2=3,36/22,4=0,15
Đặt x,y lần lượt là số mol của Al,Al2O3
2Al+6Hcl----->2AlCl3+3H2
x 3/2x
Al2O3+6Hcl---->2AlCl3+3H2O
y
=>27x+102y=5(1)
3/2x=0,15(2)
Từ (1),(2)=>x=0,1,y=0,023
%Al=0,1*27/5*100%=54%
%Al2O3=100%-54%=46%
Đúng 0
Bình luận (0)
 bài 3 câu c help pls
bài 3 câu c help pls
Giả sử d cắt trục tung tại A ; trục hoành tại B
=> Tọa độ A(0;2) ; Tọa độ B(\(\left(\dfrac{-2}{m+3};0\right)\)
SAOB = 4
=> \(\dfrac{AO.OB}{2}=4\)
=> AO.OB = 8
<=> \(2.\dfrac{-2}{m+3}=8\)
<=> \(m=-\dfrac{7}{2}\)
Đúng 0
Bình luận (0)




























