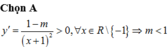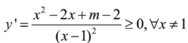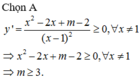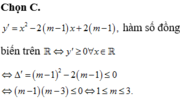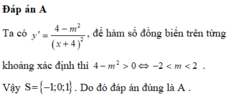Tìm tất cả các giá trị của tham số m để hàm số đồng biến trên tập xác định của nó 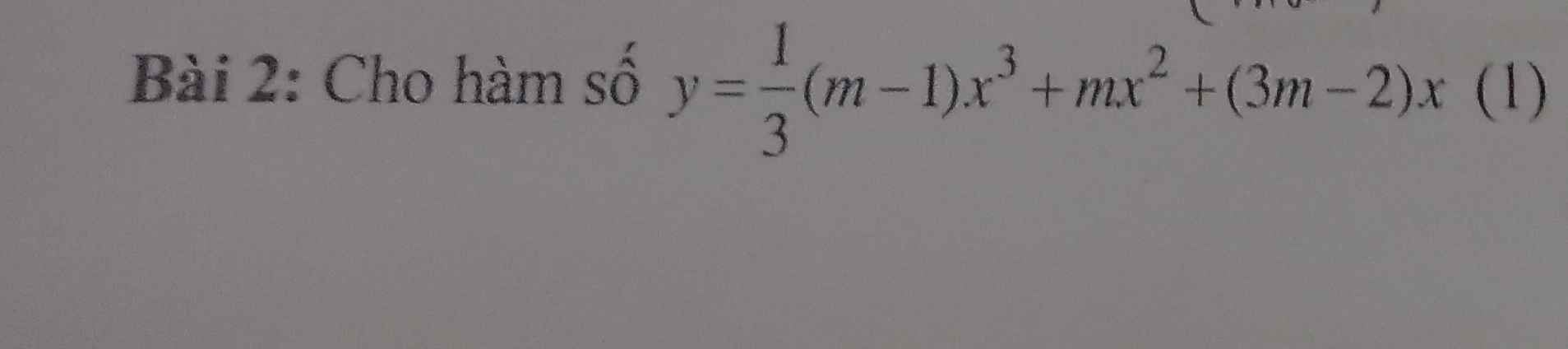

Những câu hỏi liên quan
Tìm tất cả các giá trị thực của tham số m để hàm số
y
x
+
m
x
+
1
đồng biến trên từng khoảng xác định của nó A. B. C. D.
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hàm số y = x + m x + 1 đồng biến trên từng khoảng xác định của nó
A.![]()
B. ![]()
C.![]()
D. ![]()
Tìm tất cả các giá trị thực của tham số m để hàm số
y
x
+
m
x
+
1
đồng biến trên từng khoảng xác định của nó A. m 1 B.
m
≤
1
C. m 1 D. m 1
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hàm số y = x + m x + 1 đồng biến trên từng khoảng xác định của nó
A. m < 1
B. m ≤ 1
C. m = 1
D. m > 1
Tìm tất cả các giá trị thực của tham số m để hàm số
y
2
x
−
m
x
−
1
đồng biến trên các khoảng của tập xác định. A.
m
∈
1
;
2
B.
m
∈
2
;...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hàm số y = 2 x − m x − 1 đồng biến trên các khoảng của tập xác định.
A. m ∈ 1 ; 2
B. m ∈ 2 ; + ∞
C. m ∈ 2 ; + ∞
D. m ∈ − ∞ ; 2
Đáp án C
Ta có: y ' = m − 2 x − 1 2
Hàm số đồng biến trên các khoảng xác định ⇔ y ' > 0 ⇔ m − 2 > 0 ⇔ m > 2
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị thực của tham số m để hàm số
y
x
2
-
m
x
+
2
x
-
1
đồng biến tr...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hàm số y = x 2 - m x + 2 x - 1 đồng biến trên từng khoảng xác định của nó.
A.![]()
B. m < 3
C. ![]()
D. ![]() hoặc
hoặc ![]()
Tìm tất cả các giá trị thực của tham số m để hàm số
y
x
2
-
m
x
+
2
x
-
1
đồng biến trên từng khoảng xác định của nó A.
m
≥
3
B. m 3 C.
-
2
2...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hàm số y = x 2 - m x + 2 x - 1 đồng biến trên từng khoảng xác định của nó
A. m ≥ 3
B. m < 3
C. - 2 2 ≤ m ≤ 2 2
D. m < - 2 2 hoặc m > 2 2
Cho hàm số
y
-
m
x
+
3
3
x
-
m
với m là tham số. Gọi S là tập hợp tất cả các giá trị nguyên của m để hàm số nghịch biến trên từng khoảng xác định của nó. Tìm số phần tử của tập S
Đọc tiếp
Cho hàm số y = - m x + 3 3 x - m với m là tham số. Gọi S là tập hợp tất cả các giá trị nguyên của m để hàm số nghịch biến trên từng khoảng xác định của nó. Tìm số phần tử của tập S
![]()
![]()
![]()
![]()
Cho hàm số
y
-
mx
+
3
3
x
-
m
với m là tham số. Gọi S là tập hợp tất cả các giá trị nguyên của m để hàm số nghịch biến trên từng khoảng xác định của nó. Tìm số phần tử của tập S A. 5. B. 4. C. 6. D. 8.
Đọc tiếp
Cho hàm số y = - mx + 3 3 x - m với m là tham số. Gọi S là tập hợp tất cả các giá trị nguyên của m để hàm số nghịch biến trên từng khoảng xác định của nó. Tìm số phần tử của tập S
A. 5.
B. 4.
C. 6.
D. 8.
Tìm tất cả các giá trị của m để hàm số
y
x
3
3
–
(
m
-
1
)
x
2
+
2
(
m
-
1
)
x
+
2
đồng biến trên tập xác định của nó là: A. 1 m 3 B. m ≥ 1 C. 1 ≤ m ≤ 3 D. m ≤ 3
Đọc tiếp
Tìm tất cả các giá trị của m để hàm số y = x 3 3 – ( m - 1 ) x 2 + 2 ( m - 1 ) x + 2 đồng biến trên tập xác định của nó là:
A. 1 < m < 3
B. m ≥ 1
C. 1 ≤ m ≤ 3
D. m ≤ 3
Cho hàm số y = x 2 + m x + 4 với m là tham số. Gọi S là tập hợp tất cả các giá trị nguyên của m để hàm số đồng biến trên các khoảng xác định. Tìm số phần tử của S
A. 3
B. 4
C. 5
D. Vô số
Tập hợp tất cả các giá trị thực của tham số m để hàm số
m
x
-
3
2
x
-
m
đồng biến trên cùng khoảng xác định là A.
(
-
6
;
6
]
B.
[
-
6
;
6
)
C.
[
-
6
;
6
]...
Đọc tiếp
Tập hợp tất cả các giá trị thực của tham số m để hàm số m x - 3 2 x - m đồng biến trên cùng khoảng xác định là
A. ( - 6 ; 6 ]
B. [ - 6 ; 6 )
C. [ - 6 ; 6 ]
D. ( - 6 ; 6 )
Đáp án là D.
Tập xác định: D = ℝ \ m 2 ; y , = - m 2 + 6 ( 2 x - m ) 2
Hàm số đồng biến trên từng khoảng xác định khi và chỉ khi:
y , > 0 , ∀ x ∈ D ⇔ - m 2 + 6 > 0 ⇔ m ∈ ( - 6 ; 6 ) . .
Đúng 0
Bình luận (0)