Cho ΔDEF nội tiếp (O;R). Các đường cao EK, FI cắt nhau tại H.
a) CM: tứ giác DIHK, EIKF nội tiếp.
b) CM: OD⊥IK
c) Biết cung DE 90o, cung DF là 120o.
Tính theo R diện tích hình tròn giới hạn bởi dây DE, cung EF và dây DF.
Cho ΔABC = ΔDEF. Biết A = \(55^o\), E = \(75^o\).
Tính các góc còn lại của tam giác
\(\Delta ABC=\Delta DEF\Rightarrow\left\{{}\begin{matrix}\widehat{D}=\widehat{A}=55^0\\\widehat{B}=\widehat{E}=75^0\end{matrix}\right.\)
Do tổng 3 góc trong 1 tam giác bằng 180 độ:
\(\widehat{A}+\widehat{B}+\widehat{C}=180^0\Rightarrow55^0+75^0+\widehat{C}=180^0\)
\(\Rightarrow\widehat{C}=50^0\)
\(\Rightarrow\widehat{F}=\widehat{C}=50^0\)
cho ΔABC nội tiếp đường tròn tâm (O) , (O') tiếp xúc các cạnh AB , AC tại E và F. (O') tiếp xúc với (O) tại S. gọi I là tâm của đường tròn nội tiếp ΔABC
chứng minh : BEIS , CFIS nội tiếp.
Cho tam giác ABC có độ dài các cạnh tỉ lệ với 4:5:6 . Cho biết Δ D EF ∽ Δ A B C và cạnh nhỏ nhất của Δ D E F l à 0 , 8 m , hãy tính các cạnh còn lại của Δ D E F
Vì 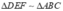 nên
nên 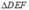 cũng có độ dài các cạnh tỉ lệ với 4 : 5 : 6.
cũng có độ dài các cạnh tỉ lệ với 4 : 5 : 6.
Giả sử DE < EF < FD Þ DE = 0,8m.
Ta có
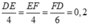
Từ đó tính được EF = 1m và FD = 1,2m
Câu 30: Cho ΔABC = ΔDEF, biết 0 A 50 = , 0 B 65 = . Hỏi ΔDEF là tam giác gì ?
ta có góc C có số đo là :
\(\widehat{C}=180^0-\widehat{A}-\widehat{B}=180^0-50^0-65^0=65^0\)
Do góc C bằng góc B nên tam giác ABC cân tại A
Do đó tam giác tương ứng là DEF cân tại đỉnh D
1) cho ΔABC ∼ ΔDEF theo tỉ số đồng dạng k=\(\dfrac{3}{2}\) . Diện tích ΔABC là 27 cm\(^2\), thi diện tích ΔDEF là:
A. 12cm\(^2\) B.24cm\(^2\) C. 36cm\(^2\) D. 18cm\(^2\)
2) ΔABC ∼ΔDEF có AB=3cm, AC=5cm, BC=7cm, DE=6cm. Ta có :
A. DF=10cm B. DF=20cm C. EF=14cm D.EF=10cm
Cho tam giác ABC nhọn, nội tiếp (O), cao AD, CE cắt nhau tại H. BO cắt DE tại I, cắt (O) tại M.
a) CM: tứ giác BEHD, AEDC nội tiếp
b) CM: DIMC nội tiếp
Cho tam giác ABC nội tiếp đường tròn (O), các đường cao AD, BE, CF cắt nhau tại H. Chứng minh a) BDEA nội tiếp b) AO cắt EF tại M, cắt (O) tại A’. CM EMA’C nội tiếp c) AD cắt EF tại Q, AA’ cắt BC tại P. CM QMPD nội tiếp d) Gọi R là giao điểm của CA’ và AH N là giao điểm của CF AA’ CM HNA’R nội tiếp
a: Xét tứ giác BDEA có
góc BDA=góc BEA=90 độ
=>BDEA là tứ giác nội tiếp
b: Kẻ tiếp tuyến Ax
=>góc xAC=góc ABC
mà góc ABC=góc AEF(=180 độ-góc FEC)
nên góc xAC=góc AEF
=>Ax//FE
=>FE vuông góc OA
Xét (O) có
ΔACA' nội tiếp
AA' là đường kính
=>ΔACA' vuông tại C
Xét tứ giác A'CEM có
góc EMA'+góc ECA'=180 độ
=>A'CEM là tứ giác nội tiếp
cho ΔABC có AB=3cm; AC=4cm; BC=5cm và ΔABC đồng dạng ΔDEF với tỉ số đồng dạng là 2. vậy chu vi ΔDEF là
Ta có:
\(\dfrac{AB}{DE}=2;\dfrac{AC}{DF}=2;\dfrac{BC}{EF}=2\)
\(\Leftrightarrow\dfrac{3}{DE}=2;\dfrac{4}{DF}=2;\dfrac{5}{EF}=2\)
\(\Leftrightarrow DE=\dfrac{3}{2};DF=\dfrac{4}{2};EF=\dfrac{5}{2}\)
\(\Rightarrow C_{DEF}=\dfrac{3}{2}+\dfrac{4}{2}+\dfrac{5}{2}=\dfrac{12}{2}=6\left(cm\right)\)
ta có : ΔABC~ΔDEF (gt)
=>\(\dfrac{AB}{DE}=\dfrac{AC}{DF}=\dfrac{BC}{\text{EF}}=k\)
=> DE = 3:2= 1,5 (cm)
DF = 4:2 = 2 (cm)
BC = 5:2 = 2,5 (cm )
=> Chu vi tam giác DEF = DE+DF+BC = 1,5+2+2,5 = 6(CM)
1.Cho ∆ABC nhọn nội tiếp trong đường tròn (O),kẽ tiếp tuyến của (O) tại A và hai đường cao BD và CE
Chứng minh:
a) tứ giác BCDE nội tiếp
b) DE song song (xy)
2.Cho ∆ABC nhọn nội tiếp trong đường tròn (O) (AB<AC).Hai đường cao BF và CE cắt nhau tại H
a) Chứng minh hai tứ giác AEHF,BEFC nội tiếp
cho tg ABC nội tiếp đường tròn (o), kẻ tiếp tuyến Ax của(o), đường thẳng song song với Ax cắt AB,AC lần lượt S,K. cm BCKS là tứ giác nội tiếp.