\(\dfrac{BC}{sinA}=\dfrac{AB}{sinC}\)

=>BC/sin120=a/sin30=2a

=>BC=a*căn 3

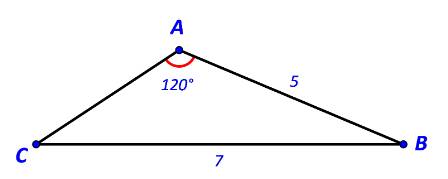
Áp dụng định lí sin trong tam giác ABC ta có:

\(\frac{{AB}}{{\sin C}} = \frac{{BC}}{{\sin A}}\)

\( \Rightarrow \sin C = \sin A.\frac{{AB}}{{BC}} = \sin {120^o}.\frac{5}{7} = \frac{{5\sqrt 3 }}{{14}}\)

\( \Rightarrow \widehat C \approx 38,{2^o}\) hoặc \(\widehat C \approx 141,{8^o}\) (Loại)

Ta có: \(\widehat A = {120^o},\widehat C = 38,{2^o}\)\( \Rightarrow \widehat B = {180^o} - \left( {{{120}^o} + 38,{2^o}} \right) = 21,{8^o}\)

Áp dụng định lí cosin trong tam giác ABC ta có:

\(\begin{array}{l}A{C^2} = A{B^2} + B{C^2} - 2.AB.BC.\cos B\\ \Leftrightarrow A{C^2} = {5^2} + {7^2} - 2.5.7.\cos 21,{8^o}\\ \Rightarrow A{C^2} \approx 9\\ \Rightarrow AC = 3\end{array}\)

Vậy độ dài cạnh AC là 3.

a) Nửa chu vi tam giác là :

\(120\div2=60\left(cm\right)\)

Độ dài đáy AC là :

\(\left(60+10\right)\div2=35\left(cm\right)\)

Độ dài đáy AB là :

\(60-35=25\left(m\right)\)

b) Chiều cao AH là :

\(60-50=10\left(m\right)\)

c) Diện tích tam giác là :

a) Tổng độ dài AC, AB là: 

\(120-50=70\left(cm\right).\)

Độ dài AC là: \(\dfrac{\left(70+10\right):2}{2}=40\left(cm\right).\)

Độ dài AB là: \(70-40=30\left(cm\right)\)

b) Diện tích tam giác ABC là: \(\dfrac{1}{2}\times AB\times AC=\dfrac{1}{2}\times30\times40=600\left(cm^2\right).\)

c) Độ dài đường cao AH là: \(600:\dfrac{1}{2}:BC=600:\dfrac{1}{2}:50=24\left(cm\right).\)

nãy tôi thử ae thôi :> 

Theo bài ra ta có : AB + AC + BC = 120 

<=> AB + AC = 70 (1) 

Lại có : AC - AB = 10 (2) 

Từ (1) ; (2) suy ra : 

\(\left\{{}\begin{matrix}AB+AC=70\\-AB+AC=10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2AC=80\\AB=AC-10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AC=40\\AB=30\end{matrix}\right.\)

b, Diện tích tam giác là : \(S=\dfrac{1}{2}.AC.AB=\dfrac{1}{2}.40.30=600cm^2\)

c, Xét tam giác ABC vuông tại A, đường cao AH

* Áp dụng hệ thức : 

\(AH.BC=AB.AC\Rightarrow AH=\dfrac{1200}{50}=\dfrac{120}{5}=24cm\)

a) Trong tam giác ABC: \(\widehat C = 180^\circ  - \widehat A - \widehat B = 180^\circ  - 42^\circ  - 37^\circ  = 101^\circ \).

b) Trong tam giác ABC: \(\widehat B < \widehat A < \widehat C\)nên \(AC < BC < AB\). (Vì AC đối diện với góc B; BC đối diện với góc A; AB đối diện với góc C).