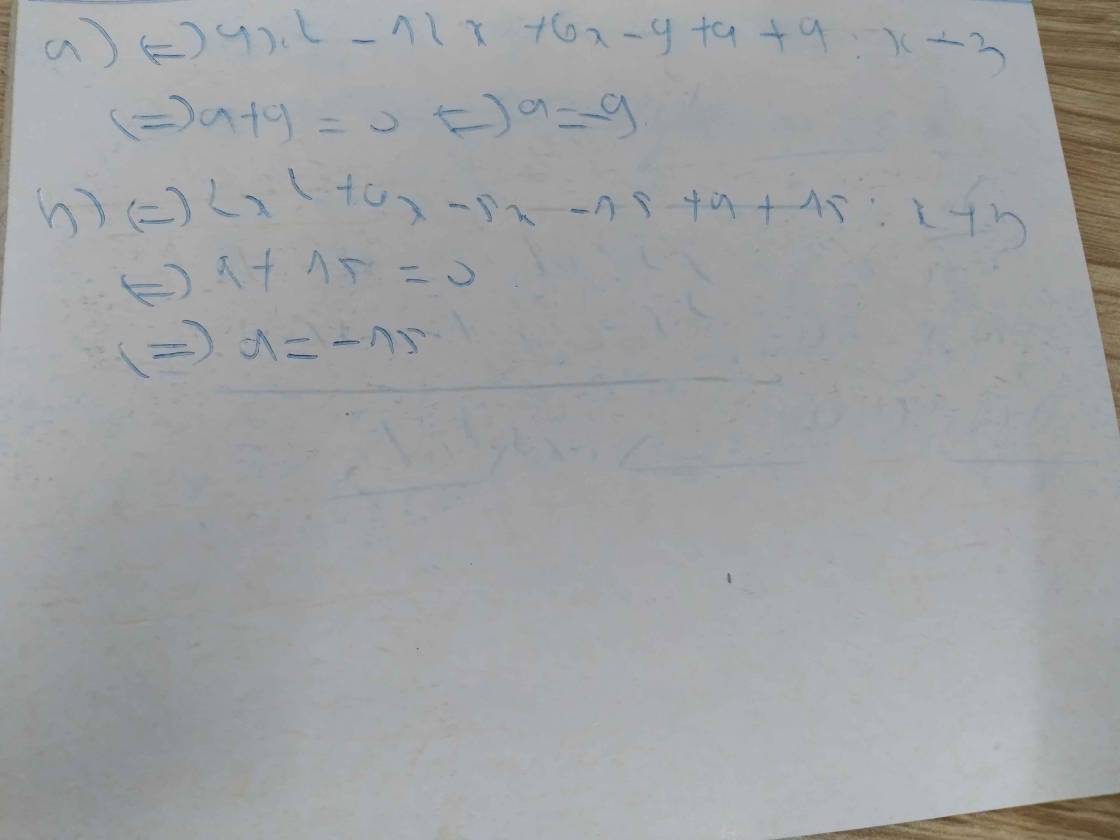Bài 2: Cho đa thức 

Những câu hỏi liên quan
Bài 10. Tìm a để
a) Đa thức 4x\(^2\) - 6x + a chia hết cho đa thức x - 3
b) Đa thức 2x\(^2\) + x + a chia hết cho đa thức x + 3
Bài 1. Tìm đa thức P(x) = x2 + ax + b. Biết rằng nghiệm của đa thức P(x) cũng là nghiệm của đa thức Q(x) = (x+2)(x-1)
Bài 2. Cho đa thức f(x) thỏa mãn f(x) + x f(-x) = x + 1 với mọi giá trị của x. Tính f(1)
Bài 3. Cho đa thức P(x) = x(x - 2) - 2x + 2m - 2015 (x là biến số, m là hằng số). Tìm m để đa thức có nghiệm.
bài 1 Tìm đa thức M sao cho tổng của M và đa thức X2- 3x2y - 7xy - 2 không chứa biến x
Bài 2 Tìm đa thức M sao cho tổng của M và đa thức X2 - 3x2y -7xy - 2 là 1 đa thức bặc 0
b) Thực hiện phép chia đa thức (2x4 – 5x3 + 2x2 +2x - 1) cho đa thức (x2 – x - 1)
Bài 2:
a) Tìm a để đa thức (2x4 + x3 - 3x2 + 5x + a) chia hết cho đa thức (x2 - x +1)
b) Tìm a để đa thức x^4 - x^3 + 6x^2 chia hết cho đa thức x^2 - x + 5
b: \(=\dfrac{2x^4-2x^3-2x^2-3x^3+3x^2+3x+x^2-x-1}{x^2-x-1}\)
\(=2x^2-3x+1\)
Đúng 0
Bình luận (0)
Bài 1:T ìm đa thức M sao cho tổng của M và đa thức x2+32y-5xy2-7xy-2 không chứa biến X
Bài 2 :Tìm đa thức M sao cho tổng của M và đa thức x2+32y-5xy2-7xy-2 là một đa thức bặc 0
mk chỉ làm đc bà 1 thôi nha
M+x2+32y-5xy2-7xy-2
=M+(x2-5xy2-7xy)+(32y-2)
Để đa thức tổng ko chứa biến x thì:
M+(x2-5xy2-7xy)=0
=> M=0-(x2-5xy2-7xy)
M=-x2-5xy2-7xy
Đúng 0
Bình luận (0)
Bài 5: Tìm a, b sao cho
a/ Đa thức x4 – x3 + 6x2 – x + a chia hết cho đa thức x2 – x + 5
b/ Đa thức 2x3 – 3x2 + x + a chia hết cho đa thức x + 2.
Đặt \(f\left(x\right)=2x^3-3x^2+x+a\)
Ta có: phép chia \(f\left(x\right)\) cho \(x+2\) có dư là \(R=f\left(-2\right)\)
\(\Rightarrow f\left(-2\right)=2.\left(-2\right)^3-3.\left(-2\right)^2+\left(-2\right)+a\)
\(f\left(-2\right)=2.\left(-8\right)-3.4-2+a\)
\(f\left(-2\right)=-16-12-2+a\)
\(f\left(-2\right)=-20+a\)
Để \(f\left(x\right)\) chia hết cho \(x+2\) thì \(R=0\) hay \(f\left(-2\right)=0\)
\(\Rightarrow-20+a=0\Leftrightarrow a=20\)
Đúng 0
Bình luận (0)
Bài 2:
a) Tìm a để đa thức (2x4 + x3 - 3x2 + 5x + a) chia hết cho đa thức (x2 - x +1)
b) Tìm a để đa thức x^4 - x^3 + 6x^2 chia hết cho đa thức x^2 - x + 5
Bài 2:
a) Tìm a để đa thức (2x4 + x3 - 3x2 + 5x + a) chia hết cho đa thức (x2 - x +1)
b) Tìm a để đa thức x^4 - x^3 + 6x^2 chia hết cho đa thức x^2 - x + 5
a: \(\Leftrightarrow2x^4-2x^3+2x^2+3x^3-3x^2+3x-2x^2+2x+2+a-2⋮x^2-x+1\)
=>a=2
Đúng 1
Bình luận (0)
Bài 1:
a)Thực hiện phép chia đa thức (2x4 – 5x3 + 2x2 +2x - 1) cho đa thức (x2 – x - 1)
b)Tìm a để đa thức x^4-x^3+6x^2-x+a chia hết cho đa thức x^2-x+5
a: \(=\dfrac{2x^4-2x^3-2x^2-3x^3+3x^2+3x+x^2-x-1}{x^2-x-1}\)
\(=2x^2-3x+1\)
Đúng 0
Bình luận (0)
Bài 2:cho đa thức A=2x^3y-3xy^2+5x^3y-xy^2+2 a)thu gọn đa thức A và xác định bậc của đa thức. b)tính giá trị của đa thức A tại x=1;y=-1
\(a,A=2x^3y-3xy^2+5x^3y-xy^2+2\\=(2x^3y+5x^3y)+(-3xy^2-xy^2)+2\\=7x^3y-4xy^2+2\)
Bậc của đa thức A: 3 + 1 = 4.
\(b,\) Thay \(x=1;y=-1\) vào \(A\), ta được:
\(A=7\cdot1^3\cdot\left(-1\right)-4\cdot1\cdot\left(-1\right)^2+2\)
\(=-7-4+2=-9\)
Đúng 1
Bình luận (0)