Cho hình vuông ABCD có cạnh AB = 4cm và hình chữ nhật MNPQ có cạnh MN = 2cm, NP = 8cm. Khi đó:
A.Diện tích hình vuông ABCD nhỏ hơn diện tích hình chữ nhật MNPQ
B.Diện tích hình vuông ABCD bằng diện tích hình chữ nhật MNPQ
C.Diện tích hình vuông ABCD lớn hơn diện tích hình chữ nhật MNPQ
D.Không so sánh được diện tích của hai hình
Cho hình chữ nhật ABCD, biết AB=8cm, AC=24cm.Tính chu vi hình chữ nhật ABCD.
Ai trả lời nhanh mình cho 1 tick.
Chu vi ABCD là: ( 8 + 24 ) x 2 = 64 cm
Cho hình chữ nhật ABCD có AB = 6 cm, BC = 8cm. M, N, P, Q là trung điểm các cạnh của hình chữ nhật. Tổng diện tích các tam giác có trong hình là:
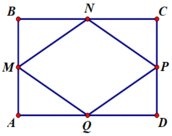
A. 4 c m 2
B. 6 c m 2
C. 12 c m 2
D. 24 c m 2
Cho hình hộp chữ nhật ABCD. MNPQ có AB = 6cm; BC = 8cm và thể tích của hình hộp là 2 40 c m 3 . Tính AA’
A. 5cm
B. 6cm
C. 8cm
D. 10cm
Thể tích của hình hộp chữ nhật là
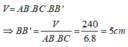
Suy ra: AA’ = BB’ =5cm
Chọn đáp án A
Cho hình chữ nhật ABCD có AB = 8cm, BD = 10cm. Trên các cạnh AB, AD lần lượt lấy các điểm E; F sao cho AE = AF = 3cm.
a, Tính diện tính của hình chữ nhật ABCD
b, Tính diện tích của đa giác EBCDF
Hình chữ nhật abcd có ab=8cm,ad=4cm.diện tích của hình chữ nhật là
Diện tích hình chữ nhật là:
8 x 4 = 32 (cm2)
Đ/S:
~ HOK TỐT ~
Cho hình chữ nhật ABCD có góc ACB =, BD=8cm. Chu vi hình chữ nhật ABCD là cm.
Cho hình chữ nhật ABCD có góc ACB =, BD=8cm. Chu vi hình chữ nhật ABCD là cm.
Cho hình chữ nhật ABCD có góc ACB =30, BD=8cm. Chu vi hình chữ nhật ABCD là cm.
Cho hình chữ nhật ABCD có AB bằng 14cm,AD bằng 20cm,BE bằng 8cm,DG bằng 9cm .Tính diện tích AECG.
Cho hình chữ nhật ABCD có chiều dài là 8cm và chu vi là 24cm. Gọi E,F,G,H lần lượt là trung điểm của các cạnh AB,BC,CD và DA. Ta có hình thoi EFGH như hình vẽ. Tính chiều rộng hình chữ nhật ABCD và diện tích hình thoi EFGH
Chiều rộng là: 24:2-8=4(cm)
EG=AD=4cm
HF=AB=8cm
\(S_{EFGH}=\dfrac{1}{2}\cdot4\cdot8=16\left(cm^2\right)\)
AHB // 
