a. u1 = - 1, un + 1 = un + 3 với n > 1

u1 = - 1;

u2 = u1 + 3 = -1 + 3 = 2

u3 = u2 + 3 = 2 + 3 = 5

u4 = u3 + 3 = 5 + 3 = 8

u5 = u4 + 3 = 8 + 3 = 11

b. Chứng minh phương pháp quy nạp: un = 3n – 4 (1)

+ Khi n = 1 thì u1 = 3.1 - 4 = -1, vậy (1) đúng với n = 1.

+ Giả sử công thức (1) đúng với n = k > 1 tức là uk = 3k – 4.

+ Ta chứng minh (1) đúng với n= k+ 1 tức là chứng minh: uk+1 = 3(k+1) - 4

Thật vậy,ta có : uk + 1 = uk + 3 = 3k – 4 + 3 = 3(k + 1) – 4.

⇒ (1) đúng với n = k + 1

Vậy (1) đúng với ∀ n ∈ N*.

Bước 1: Xác định đầu vào và đầu ra của chương trình.

Đầu vào: Dãy số A gồm n phần tử (A[0], A[1], ..., A[n-1]).

Đầu ra: Một câu trả lời là "có" nếu trong dãy A có hai phần tử trùng nhau, hoặc "không" nếu không có.

Bước 2: Xác định giải thuật kiểm tra trùng nhau.

Giải thuật đơn giản nhất là duyệt qua từng phần tử của dãy A, so sánh nó với các phần tử trước đó trong dãy để tìm kiếm phần tử trùng nhau.

Bước 3: Thiết kế mã nguồn chương trình.

Sử dụng một vòng lặp for để duyệt qua từng phần tử của dãy A từ đầu đến cuối.

Trong mỗi lần lặp, so sánh phần tử hiện tại (A[i]) với các phần tử trước đó (A[0], A[1], ..., A[i-1]) để kiểm tra xem có phần tử trùng nhau hay không.

Nếu tìm thấy phần tử trùng nhau, đưa ra kết quả là "có" và kết thúc chương trình.

Nếu không tìm thấy phần tử trùng nhau sau khi đã duyệt qua toàn bộ dãy A, đưa ra kết quả là "không".

def check_duplicate(A):

 for i in range(len(A)):

  for j in range(i + 1, len(A)):

   if A[i] == A[j]:

    return "có"

 return "không"

# Đầu vào: Dãy số A

A = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]

# Gọi hàm để kiểm tra

result = check_duplicate(A)

# Đầu ra: Kết quả kiểm tra

print(result)

def is_prime(num):

      if num < 2:

            return False

      for i in range(2, int(num ** 0.5) + 1):

            if num % i == 0:

                  return False

            return True

def is_fibonacci(num):

      if num == 0 or num == 1:

            return True

      x = 0

      y = 1

      while y < num:

            z = x + y

            x = y

            y = z

      if y == num:

            return True

      else:

            return False

n = int(input("Nhập số phần tử của dãy: "))

arr = [ ]

for i in range(n):

      num = int(input(f"Nhập phần tử thứ {i+1}: "))

      arr.append(num)

sum = 0

for num in arr:

      if is_prime(num) and is_fibonacci(num):

            sum += num

print(f"Tổng các phần tử vừa là số nguyên tố vừa là số fibonacci trong dãy là: {sum}")

a. Năm số hạng đầu của dãy số

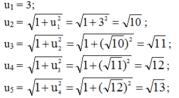
b. Dự đoán công thức số hạng tổng quát của dãy số:

un =√(n+8) (1)

Rõ ràng (1) đúng với n = 1

Giả sử (1) đúng với n = k, nghĩa là uk = √(k+8)

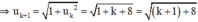
⇒ (1) đúng với n = k + 1

⇒ (1) đúng với mọi n ∈ N*.

a. 5 số hạng đầu dãy là:

u1 = 2;

u2 = 2u1 – 1 = 3;

u3 = 2u2 – 1 = 5;

u4 = 2u3 – 1 = 9;

u5 = 2u4 – 1 = 17

b. Chứng minh un = 2n – 1 + 1 (1)

+ Với n = 1 ⇒ u1 = 21 - 1 + 1 = 2 (đúng).

+ Giả sử (1) đúng với n = k ≥ 1, tức là uk = 2k-1 + 1 (1)

Ta chứng minh: uk+1 = 2k + 1. Thật vậy, ta có:

⇒ uk+1 = 2.uk – 1 = 2(2k-1 + 1) – 1 = 2.2k – 1 + 2 – 1 = 2k + 1

⇒ (1) cũng đúng với n = k + 1 .

Vậy un = 2n – 1 + 1 với mọi n ∈ N.

ai đó giúp mình với nhanh lên

thêm test đây nha:

Dữ liệu : Vào từ từ tệp Suaxau.Inp chứa xâu cần sửa. 

Kết quả:  Ghi vào tệp Suaxau.out xâu đã sửa. 

Ví dụ: 

https://youtu.be/b5YcStwxIiM

#include <bits/stdc++.h>

using namespace std;

long long a[1000],i,n,x;

int main()

{

cin>>n;

for (i=1; i<=n; i++) cin>>a[i];

sort(a+1,a+n+1);

for (i=1; i<=n; i++)

{

int x=sqrt(a[i]);

if (x*x==a[i]) 

{

cout<<x;

return 0;

}

}

cout<<"Ko co so chinh phuong trong day";

return 0;

}

uses crt;
var x，i，max，n，dem，dem1，dem2，dem3，t，t1:integer;
a，b，c，d，e:array[-32000..32000]of integer;
tbca，tbcd:real;
begin
clrscr;
write(‘n=’); readln(n);
for i:=1 to n do
begin
write(‘a[‘，i，’]=’); readln(a[i]);
inc(b[a[i]]);
end;
{———————————-cau-a—————————-}
max:=0;
for i:=1 to n do
if max<b[a[i]] then
begin
max:=b[a[i]];
x:=a[i];
end;
writeln(‘phan tu co so lan xuat hien nhieu nhat trong mang la: ‘，x);
{——————————–cau-b——————————-}
dem:=0;
for i:=1 to n do
if a[i]>=0 then
begin
dem:=dem+1;
c[dem]:=a[i];
end;
dem1:=0;
for i:=1 to dem do
if trunc(sqrt(c[i]))=sqrt(c[i]) then inc(dem1);
writeln(‘so luong so chinh phuong trong day la: ‘，dem1);
{——————————–cau-c—————————–}
dem2:=0;
dem3:=0;
for i:=1 to n do
begin
if a[i]>0 then
begin
inc(dem2);
d[dem2]:=a[i];
end;
if a[i]<0 then
begin
inc(dem3);
e[dem3]:=a[i];
end;
end;
t:=0;
t1:=0;
for i:=1 to dem2 do
t:=t+d[i];
tbcd:=t/dem2;
for i:=1 to dem3 do
t1:=t1+e[i];
tbca:=t1/dem3;
writeln(‘trung binh cong cac so am la: ‘，tbca:4:2);
writeln(‘trung binh cong cac so duong la: ‘，tbcd:4:2);
readln;
end.

thấy bạn tự ra đề tự làm mà

uses crt;

var a:array[1..100] of integer;

i,n,ln:integer;

begin

clrscr;

readln(n);

for i:=1 to n do

readln(a[i]);

ln:=0;

for i:=1 to n do

if trunc(sqrt(A[i]))=sqrt(a[i]) then 

begin

write(a[i]:4);

if ln<A[i] then ln:=A[i];

end;

writeln;

writeln('So chinh phuong lon nhat la: ',ln);

readln;

end.

Để giải quyết bài toán này, chúng ta có thể sử dụng vòng lặp để duyệt qua từng phần tử trong dãy số và kiểm tra xem phần tử đó có phải là số chính phương hay không. Nếu là số chính phương, ta in ra phần tử đó và cập nhật tích tích các số chính phương.

Dưới đây là code mẫu để giải quyết bài toán này:

```
#include <iostream>
#include <math.h>

using namespace std;

int main()
{
int n;
cout << "Nhap so phan tu cua day: ";
cin >> n;

int a[n]; cout &lt;&lt; &quot;Nhap cac phan tu cua day: &quot;; for (int i = 0; i &lt; n; i++) { cin &gt;&gt; a[i]; } int tich = 1; cout &lt;&lt; &quot;Cac so chinh phuong trong day la: &quot;; for (int i = 0; i &lt; n; i++) { if (sqrt(a[i]) == floor(sqrt(a[i]))) { cout &lt;&lt; a[i] &lt;&lt; &quot; &quot;; tich *= a[i]; } } cout &lt;&lt; endl &lt;&lt; &quot;Tich cac so chinh phuong la: &quot; &lt;&lt; tich; return 0;

}
```

Trong đoạn code trên, chúng ta sử dụng hàm `sqrt()` để tính căn bậc hai của mỗi phần tử trong dãy số. Nếu kết quả là một số nguyên, tức là phần tử đó là số chính phương, ta in ra và cập nhật tích.