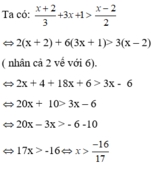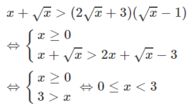Giải bất phương trình:18-3x(1-x)

Những câu hỏi liên quan
1.Giải các phương trình sau : a,7x+35=0 b, 8-x/x-7 -8 =1/x-7 2.giải bất phương trình sau : 18-3x(1-x)_< 3x^2-3x
a: 7x+35=0
=>7x=-35
=>x=-5
b: \(\dfrac{8-x}{x-7}-8=\dfrac{1}{x-7}\)
=>8-x-8(x-7)=1
=>8-x-8x+56=1
=>-9x+64=1
=>-9x=-63
hay x=7(loại)
Đúng 1
Bình luận (0)
a, \(7x=-35\Leftrightarrow x=-5\)
b, đk : x khác 7
\(8-x-8x+56=1\Leftrightarrow-9x=-63\Leftrightarrow x=7\left(ktm\right)\)
vậy pt vô nghiệm
2, thiếu đề
Đúng 0
Bình luận (0)
1.
\(a,7x+35=0\\ \Rightarrow7x=-35\\ \Rightarrow x=-5\\ b,ĐKXĐ:x\ne7\\ \dfrac{8-x}{x-7}-8=\dfrac{1}{x-7}\\ \Leftrightarrow\dfrac{8-x}{x-7}-\dfrac{8\left(x-7\right)}{x-7}-\dfrac{1}{x-7}=0\\ \Leftrightarrow\dfrac{8-x-8x+56-1}{x-7}=0\\ \Rightarrow-9x+63=0\\ \Leftrightarrow-9x=-63\\ \Leftrightarrow x=7\left(ktm\right)\)
2.đề thiếu
Đúng 0
Bình luận (0)
Bài 1: Giải các bất phương trình:
3(1 - x)> \(\dfrac{7-3x^2}{x+1}\)
Bài 2. Giải và biện luận bất phương trình
( m2 - 4 ) x +3 > ( 2m -1) x +m
cho hàm số \(f\left(x\right)=x^3-3x^2+2\)
a, giải bất phương trình \(f'\left(x\right)\le0\)
b, giải phương trình \(f'=\left(x^2-3x+2\right)=0\)
c, đặt \(g\left(x\right)=f\left(1-2x\right)+x^2-x+2022\) giải bất phương trình\(g'\left(x\right)\ge0\)
\(a,f'\left(x\right)=3x^2-6x\\ f'\left(x\right)\le0\Leftrightarrow3x^2-6x\le0\\ \Leftrightarrow3x\left(x-2\right)\le0\Leftrightarrow0\le x\le2\)
Đúng 2
Bình luận (0)
Lời giải:
a. $f'(x)\leq 0$
$\Leftrightarrow 3x^2-6x\leq 0$
$\Leftrightarrow x(x-2)\leq 0$
$\Leftrightarrow 0\leq x\leq 2$
b.
$f'(x)=x^2-3x+2=0$
$\Leftrightarrow 3x^2-6x=x^2-3x+2=0$
$\Leftrightarrow 3x(x-2)=(x-1)(x-2)=0$
$\Leftrightarrow x-2=0$
$\Leftrightarrow x=2$
c.
$g(x)=f(1-2x)+x^2-x+2022$
$g'(x)=(1-2x)'f(1-2x)'_{1-2x}+2x-1$
$=-2[3(1-2x)^2-6(1-2x)]+2x-1$
$=-24x^2+2x+5$
$g'(x)\geq 0$
$\Leftrightarrow -24x^2+2x+5\geq 0$
$\Leftrightarrow (5-12x)(2x-1)\geq 0$
$\Leftrightarrow \frac{-5}{12}\leq x\leq \frac{1}{2}$
Đúng 1
Bình luận (0)
Áp dụng quy tắc nhân, giải các bất phương trình sau: 3x < 18
Ta có: 3x < 18
![]()
Vậy tập nghiệm của bất phương trình là: {x|x < 6}
Đúng 0
Bình luận (0)
Cho bất phương trình
3
+
x
+
6
-
x
-
18
+
3
x
-
x
2
≤
m
2
-
m
+
1
(m là tham số). Có bao nhiêu giá trị nguyên của m thuộc[-5;5] để bất phương trình nghiệm đúng với mọi...
Đọc tiếp
Cho bất phương trình 3 + x + 6 - x - 18 + 3 x - x 2 ≤ m 2 - m + 1 (m là tham số). Có bao nhiêu giá trị nguyên của m thuộc[-5;5] để bất phương trình nghiệm đúng với mọi x ∈ - 3 ; 6 ?
A. 3
B. 5
C. 9
D. 10
Đặt ![]()
Suy ra ![]()
Ta có ![]()
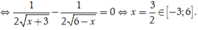
Ta có bảng biến thiên
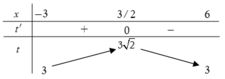
Từ bảng biến thiên ta suy ra ![]()
Khi đó bất phương trình trở thành: ![]()
![]()
Xét hàm số ![]() với
với ![]()
Ta có ![]()
Suy ra hàm số f(t) nghịch biến trên ![]()
![]()
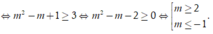
Chọn C.
Đúng 0
Bình luận (0)
Bài I: 1) Giải các phương trình a/8 + 4x = 3x – 1
2) Giải các bất phương trình a) 10 - 5(x + 3) > 3(x - 1)
1) Ta có: \(4x+8=3x-1\)
\(\Leftrightarrow4x-3x=-1-8\)
\(\Leftrightarrow x=-9\)
2) Ta có: \(10-5\left(x+3\right)>3\left(x-1\right)\)
\(\Leftrightarrow10-5x-15-3x+3>0\)
\(\Leftrightarrow-8x>2\)
hay \(x< \dfrac{-1}{4}\)
Đúng 1
Bình luận (0)
Giải bất phương trình:
x
+
2
3
+
3
x
+
1
x
-
2
2
A.
x
-
16
17
B.
x
6
17
C.
x
-
16
17
D. ...
Đọc tiếp
Giải bất phương trình: x + 2 3 + 3 x + 1 > x - 2 2
A. x < - 16 17
B. x > 6 17
C. x > - 16 17
D. x > - 6 11
Bài 3 :Cho bất phương trình : 3x(2x + 5) x(6x -1) + 4a) Giải bất phương trình và biểu diễn tập nghiệm trên trục số.b) Tìm nghiệm nguyên nhỏnhất của bất phương trình trên.
Đọc tiếp
Bài 3 :Cho bất phương trình : 3x(2x + 5) x(6x -1) + 4
a) Giải bất phương trình và biểu diễn tập nghiệm trên trục số.
b) Tìm nghiệm nguyên nhỏnhất của bất phương trình trên.
Giải các bất phương trình sau:
x + x > 2 x + 3 x - 1