Cho ABCD là tứ giác nội tiếp đường tròn biết góc A=55°, góc D=65°. Hãy tính góc C, góc B?

Những câu hỏi liên quan
Cho ABCD là tứ giác nội tiếp đường tròn biết góc A = 80°, góc B = 60°. Hãy tính góc C, góc D
Ta có:
\(\widehat{A}+\widehat{C}=180^o\) ( góc đối của tứ giác nội tiếp )
\(\Rightarrow\widehat{C}=180^o-80^o=100^o\)
Ta có:
\(\widehat{B}+\widehat{D}=180^o\) ( góc đối của tứ giác nội tiếp )
\(\Rightarrow\widehat{D}=180^o-60^o=120^o\)
Đúng 1
Bình luận (0)
Cho tứ giác ABCD nội tiếp trong đường tròn biết A^ = 75 độ ; B= 60 độ . Tình số đo góc C và góc D
Vì tứ giác ABCD nội tiếp (O)
=> góc B + góc C = 180 độ (tổng 2 góc đối bằng 180 độ)
=> 60 + góc C = 180
=> góc C = 180 - 60 = 120 độ
Tiếp tục, ta cũng có góc A + góc D = 180 độ
=> 75 + góc D = 180
=> góc D = 180 - 75 = 105 độ
Note: Bài này đoạn kết còn có cách tính khác, cần inbox mình
Đúng 0
Bình luận (0)
Theo mk thi: goc C=105° va goc D=120°
Aj thay dung thj ung ho mk nha!!! Cam on.
Đúng 0
Bình luận (0)
Ban Vu Nhu Mai ve hinh nhu the thi se la tu giac ABDC ( saj de bai)
De bai la tu giac ABCD .
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Cho tứ giác ABCD nội tiếp đường tròn tâm O. Biết \(\dfrac{B}{D}\)=\(\dfrac{2}{3}\). Tính góc B và góc D.
Mn giúp mình với
Do tứ giác ABCD nội tiếp \(\Rightarrow B+D=180^0\) (1)
Mà \(\dfrac{B}{D}=\dfrac{2}{3}\Rightarrow B=\dfrac{2}{3}D\)
Thế vào (1):
\(\dfrac{2}{3}D+D=180^0\Rightarrow\dfrac{5}{3}D=180^0\)
\(\Rightarrow D=108^0\)
\(B=\dfrac{2}{3}D=\dfrac{2}{3}.108^0=72^0\)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A. Trên cạnh AC lấy điểm M. Vẽ đường tròn đường kính MC. Kẻ BM cắt đường tròn tại D. Đường thẳng DA cắt đường tròn tại S. Chứng minh rằng :
a) Tứ giác ABCD nội tiếp được đường tròn
b) Góc ACB = góc ACS
c) Tính diện tích và chu vi của đường tròn ngoại tiếp tứ giác ABCD, biết AB= 9cm, AC= 12 cm
Cho hình thang ABCD nội tiếp đường tròn ( O) có đường chéo AC, BD cắt nhau ở E, các cạnh bên AD, BC kéo dài cắt nhau ở F. Chứng minh rằng: a, Tứ giác ABCD là hình thang cân b, FA.FD=FB.FC c, Góc AED = góc AOD d, Tứ giác AOCF nội tiếp
b) Xét ΔFDC có
A\(\in\)FD(gt)
B\(\in\)FC(gt)
AB//CD(gt)
Do đó: \(\dfrac{FA}{AD}=\dfrac{FB}{BC}\)(Định lí Ta lét)
\(\Leftrightarrow\dfrac{FA}{FB}=\dfrac{AD}{BC}=1\)
hay FA=FB
Ta có: FA+AD=FD(A nằm giữa F và D)
FB+BC=FC(B nằm giữa F và C)
mà FA=FB(cmt)
và AD=BC(ABCD là hình thang cân)
nên FD=FC
Ta có: FA=FB(cmt)
FD=FC(cmt)
Do đó: \(FA\cdot FD=FB\cdot FC\)(đpcm)
Đúng 1
Bình luận (0)
a) Ta có: ABCD là tứ giác nội tiếp(gt)
nên \(\widehat{A}+\widehat{C}=180^0\)(hai góc đối)(1)
Ta có: ABCD là hình thang(AB//CD)
nên \(\widehat{A}+\widehat{D}=180^0\)(hai góc trong cùng phía)(2)
Từ (1) và (2) suy ra \(\widehat{C}=\widehat{D}\)
Hình thang ABCD(AB//CD) có \(\widehat{C}=\widehat{D}\)(cmt)
nên ABCD là hình thang cân(Dấu hiệu nhận biết hình thang cân)
Đúng 0
Bình luận (0)
 cho tứ giác ABCD nội tiếp đường tròn (O) . Biết góc A= 80 độ , B= 125 độ
cho tứ giác ABCD nội tiếp đường tròn (O) . Biết góc A= 80 độ , B= 125 độ
a) tính sđBD và góc AOC
b) kẻ tiếp tuyến Ax của (O) tính góc CAx
Cho tam giác ABC vuông ở A. Trên AC lấy một điểm M và vẽ đường tròn đường kính MC. Kẻ BM cắt đường tròn tại D. Đường thẳng DA cắt đường tròn tại S. Chứng minh rằng:
a) ABCD là một tứ giác nội tiếp
b) góc ABD bằng góc ACD
c) CA là tia phân giác của góc SCB
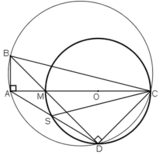
a) 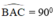 ⇒ A ∈ đường tròn đường kính BC.
⇒ A ∈ đường tròn đường kính BC.
D ∈ đường tròn đường kính MC

⇒ D ∈ đường tròn đường kính BC
⇒ A, B, C, D cùng thuộc đường tròn đường kính BC
hay tứ giác ABCD nội tiếp.
b) Xét đường tròn đường kính BC:
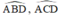 đều là góc nội tiếp chắn cung
đều là góc nội tiếp chắn cung 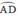
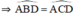
c) + Trong đường tròn đường kính MC:
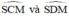 đều là các góc nội tiếp cùng chắn cung
đều là các góc nội tiếp cùng chắn cung 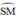
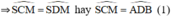
+ Trong đường tròn đường kính BC:
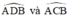 đều là các góc nội tiếp chắn cung
đều là các góc nội tiếp chắn cung 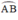
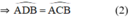

Đúng 1
Bình luận (0)
Bài 5:Cho tam giác ABC cân tại A nội tiếp đường tròn tâm O,các đường cao AG,BE,CF cắt nhau tại H
a)Chứng minh tứ giác AEHF nội tiếp đường tròn,
b)Từ B kẻ tiếp tuyến Bx của đường tròn.Hãy tính góc ABC khi góc bằng 65 độ
có \(\widehat{AEH}=90\)
\(\widehat{AFH}\)=90
\(\widehat{AEH}+\widehat{AFH}=90+90=180\) tổng 2 góc đối nhau
⇒ tứ giác AEHF là tứ giác nội tiếp
Đúng 1
Bình luận (0)
Cho tứ giác ABCD nội tiếp đường tròn tâm O đường kính AD hai đường chéo AC và BD cắt nhau tại E kẻ EF vuông góc ad a) Chứng minh tứ giác ECDF nội tiếp Xác định tâm I b) Chứng minh CA là phân giác của góc BCF c) Chứng minh tứ giác bcef nội tiếp
a) Xét (O) có
ΔACD nội tiếp đường tròn(A,C,D\(\in\)(O))
AD là đường kính(gt)
Do đó: ΔACD vuông tại C(Định lí)
Suy ra: AC\(\perp\)CD tại C
hay \(EC\perp CD\) tại C
Xét tứ giác ECDF có
\(\widehat{EFD}\) và \(\widehat{ECD}\) là hai góc đối
\(\widehat{EFD}+\widehat{ECD}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: ECDF là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
Đúng 0
Bình luận (0)





















