Vẽ tam giác ABC có độ dài các cạnh là:AB=4cm;AC=8cm và AD là đường phân giác của góc A.
Tính tỉ số diện tích của tam giác ABD và diện tích của tam giác ACD

Những câu hỏi liên quan
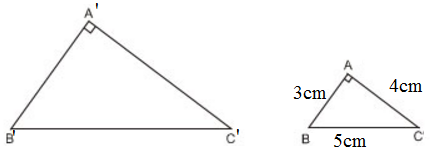
Tam giác ABC có độ dài các cạnh là 3cm, 4cm, 5cm. Tam giác A'B'C' đồng dạng với tam giác ABC và có diện tích là 54cm2. Tính độ dài các cạnh của tam giác A'B'C'.
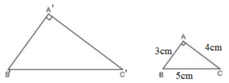
Xét ΔABC có: AB2 + AC2 = 32 + 42 = 25 = 52 = BC2
⇒ ΔABC vuông tại A (Định lý Pytago đảo)
⇒ Diện tích tam giác ABC bằng:
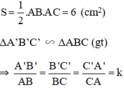
(với k là tỉ số đồng dạng).
Lại có tỉ số diện tích bằng bình phương tỉ số đồng dạng
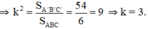
⇒ A’B’ = 3.AB = 3.3 = 9 (cm)
B’C’ = 3.BC = 3.5 = 15 (cm)
C’A’ = 3.CA = 3.4 = 12 (cm)
Vậy độ dài ba cạnh của tam giác lần lượt là 9cm, 12cm, 15cm.
Đúng 0
Bình luận (0)
Cho tam giác ABC có cạnh huyền BC = 4cm. độ dài các cạnh góc vuông tỉ lệ với 3 và 4. Tính độ dài các cạnh của tam giác ?
Theo bài ra ta có: Độ dài các cạnh góc vuông tỉ lệ với 3 và 4. Nên ta có:
\(\frac{AB}{3}=\frac{AC}{4}\) \(\Rightarrow\left(\frac{AB}{3}\right)^2=\left(\frac{AC}{4}\right)^2\) \(\Rightarrow\frac{AB^2}{9}=\frac{AC^2}{16}\)
Theo định lí Py-ta-go, tam giác vuông ABC có cạnh huyền BC \(\Rightarrow AB^2+AC^2=BC^2=4^2=16\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta được:
\(\frac{AB^2}{9}=\frac{AC^2}{16}=\frac{AB^2+AC^2}{9+16}=\frac{16}{25}\)
\(\Rightarrow\frac{AB^2}{9}=\frac{16}{25}\Rightarrow AB^2=5,76\Rightarrow AB=2,4\left(cm\right)\)
\(\frac{AC^2}{16}=\frac{16}{25}\Rightarrow AC^2=10,24\Rightarrow AC=3,2\left(cm\right)\)
Vậy AB = 2,4 cm
AC = 3,2 cm
BC = 4 cm
Đúng 0
Bình luận (0)
Vẽ tam giác ABC, có góc B= 60 độ, BC= 4cm, góc C=30 độ. Hỏi độ dài cạnh AB
Xét ΔABC có:
ˆA=ˆB+ˆC=60o+30o=90o
⇒ΔABC vuông tại A
Có AB là góc đối diện với ˆC=30o
⇒AB=12BC=12.4=2(cm)
Vậy AB=2cm
Đúng 1
Bình luận (0)
Cho tam giác ABC có độ dài các cạnh
A
B
4
c
m
,
A
C
5
c
m
v
à
B
C
6
c
m
và tam giác MNP có độ dài các cạnh
M
N
3
c
m
,
M
P
2
c
m
,
N
P
...
Đọc tiếp
Cho tam giác ABC có độ dài các cạnh A B = 4 c m , A C = 5 c m v à B C = 6 c m và tam giác MNP có độ dài các cạnh M N = 3 c m , M P = 2 c m , N P = 2 , 5 c m thì:
A. S A B C S M N P = 4
B. S M N P S A B C = 1 2
C. S M N P S A B C = 1 3
Tam giác ABC có độ dài các cạnh là 3cm, 4cm, 5cm. Tam giác A'B'C' đồng dạng với tam giác ABC và có diện tích là \(54m^2\). Tính độ dài các cạnh của tam giác A'B'C' ?
a) Cho đoạn thẳng BC = 4cm. Vẽ tam giác đều ABC. Có thể vẽ được bao nhiêu tam giác như vậy? b) Cho BC = 4cm. Vẽ hình vuông ABCD. Có thể vẽ được bao nhiêu hình vuông như vậy? c) Vẽ hình chữ nhật có một cạnh dài 6cm; một cạnh dài 4 cm d) Vẽ hình thoi có cạnh bằng 3 cm và độ dài đường chéo bằng 6cm
Cho tam giác ABC có độ dài các cạnh
A
B
8
c
m
,
A
C
7
c
m
,
B
C
4
c
m
.
So sánh các góc của tam giác ABC. A. ∠B ∠A ∠C B. ∠C ∠B ∠A C. ∠C ∠A ∠B D. ∠C ∠B ∠A
Đọc tiếp
Cho tam giác ABC có độ dài các cạnh A B = 8 c m , A C = 7 c m , B C = 4 c m . So sánh các góc của tam giác ABC.
A. ∠B > ∠A > ∠C
B. ∠C < ∠B < ∠A
C. ∠C > ∠A > ∠B
D. ∠C > ∠B > ∠A
Vì BC < AC < AB ⇒ ∠A < ∠B < ∠C hay ∠C > ∠B > ∠A . Chọn D
Đúng 0
Bình luận (0)
Tam giác \(ABC\) có độ dài \(AB = 4cm,AC = 6cm,BC = 9cm.\)Tam giác \(A'B'C'\) đồng dạng với tam giác \(ABC\) và có chu vi bằng 66,5 cm. Hãy tính độ dài các cạnh của tam giác \(A'B'C'\).
Vì tam giác \(ABC\) đồng dạng với tam giác \(A'B'C'\) nên tam giác \(A'B'C'\) đồng dạng với tam giác \(ABC\). Do đó, \(\frac{{A'B'}}{{AB}} = \frac{{B'C'}}{{BC}} = \frac{{A'C'}}{{AC}}\) (các cặp cạnh tương ứng có cùng tỉ lệ)
Thay số, \(\frac{{A'B'}}{4} = \frac{{B'C'}}{9} = \frac{{A'C'}}{6}\). Áp dụng tính chất dãy tỉ số bằng nhau ta được:
\(\frac{{A'B'}}{4} = \frac{{B'C'}}{9} = \frac{{A'C'}}{6} = \frac{{A'B' + B'C' + A'C'}}{{4 + 6 + 9}} = \frac{{66,5}}{{19}} = 3,5\)
Ta có:
\(\left\{ \begin{array}{l}\frac{{A'B'}}{4} = 3,5 \Rightarrow A'B' = 3,5.4 = 14\\\frac{{A'C'}}{6} = 3,5 \Rightarrow A'C' = 3,5.6 = 21\\\frac{{B'C'}}{9} = 3,5 \Rightarrow B'C' = 3,5.9 = 31,5\end{array} \right.\)
Vậy \(A'B' = 14cm,A'C' = 21cm,B'C' = 31,5cm\).
Đúng 0
Bình luận (0)
Vẽ tam giác ABC, biết độ dài các cạnh AB=3cm, AC=4cm, BC=5cm. Góc BAC bằng bao nhiêu độ
Ta có \(AB^2+AC^2=3^2+4^2=25\)
\(BC^2=5^2=25\)
\(\Rightarrow AB^2+AC^2=BC^2\)Áp dụng pi- ta - go đảo ta có :
\(\Delta ABC\)vuông tại A
\(\Rightarrow\widehat{BAC}=90^o\)
Đúng 0
Bình luận (0)
NHẬN XÉT \(AB^2+AC^2=3^2+4^2=25=5^2=BC^2\)
Nên áp dụng định lý Pytago đảo ta có tam giác ABC vuông tại A
Vậy góc BAC bằng \(90^o\)
Đúng 0
Bình luận (0)
Ta thấy:AB^2+AC^2=3^2+4^2=9+16=25
BC^2=5^2=25
=>AB^2+AC^2=BC^2(=25)
=>Tam giác ABC vuông tại A(theo định lý Pi ta go đảo)
=>Góc BAC=90 độ
Vậy góc BAC=90 độ
Đúng 0
Bình luận (0)