Cho tam giác ABC, kẻ AH vuông góc BC, điểm H thuộc BC, kết luận nào là chính xác nhất GIÚP EM VS

Những câu hỏi liên quan
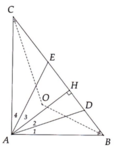
cho tam giác nhọn ABC. ở phía ngoài tam giác ABC, vẽ các tam giác vuông cân tại A là ABD và AEC. kẻ AH vuông góc BC( H thuộc BC). gọi I là giao điểm của HA và DE
a) Kẻ DN và EM vuông góc vs HA (N,M thuộc HA). Chứng minh rằng DN=AH, EM=AH
b) Chứng minh rằng DI=IE
cho tam giác ABC có AB=AC , từ A kẻ AH vuông góc BC (H thuộc BC).
a, vẽ hình ghi giả thiết, kết luận.
b, CMR: tam giác AHB = tam giác AHC
c, CMR: AH vuông góc với BC
d, Trên tia đối của tia AH lấy điểm E .CMR : BE = EC.
giúp mình với , nhanh lên nhé mình tick cho
cho tam giác ABC có AB=AC , từ A kẻ AH vuông góc BC (H thuộc BC).
a, vẽ hình ghi giả thiết, kết luận.
b, CMR: tam giác AHB = tam giác AHC
c, CMR: AH vuông góc với BC
d, Trên tia đối của tia AH lấy điểm E.CMR : BE = EC
Cho tam giác ABC vuông tại A. Kẻ AH vuông góc với BC, H thuộc BC. Tia phân giác của góc
H
A
B
^
cắt BC tại D, tia phân giác của góc
H
A
C
^
cắt BC tại E. Chứng minh điểm cách đều ba cạnh của tam giác ABC chính là điểm cách đều ba đỉnh của tam giác ADE.
Đọc tiếp
Cho tam giác ABC vuông tại A. Kẻ AH vuông góc với BC, H thuộc BC. Tia phân giác của góc H A B ^ cắt BC tại D, tia phân giác của góc H A C ^ cắt BC tại E. Chứng minh điểm cách đều ba cạnh của tam giác ABC chính là điểm cách đều ba đỉnh của tam giác ADE.
Cho tam giác nhọn ABC. Ở ngoài tam giác ABC, vẽ các tam giác vuông cân tại A là ABD và ACE. Kẻ AH vuông góc với BC (H thuộc BC). Gọi I là giao điểm của HA và DE.
a) Kẻ DN và EM vuông góc với HA (N, M thuộc HA). CMR: DN=AH, EM=AH.
b) CMR: DI=IE.
Mn giúp mk với
Cho tam giác ABC có AB = AC = 5cm, BC = 6cm. Kẻ AH vuông góc BC ( H thuộc BC)
a) chứng minh tam giác ABH = tam giác ACH
b) Tính độ dài AH
c) Từ H kẻ HD vuông góc với AB (D thuộc AB) kẻ HE vuông góc vs AC ( E thuộc AC). Chứng minh AH là đường trung trục của DE
Cho tam giác ABC có AB AC 10cm, BC12cm,kẻ AH vuông góc vs BC tại H 1. Chứng minh tam giác ABHACH và H là trung điểm của BC 2. Tính AH? 3. Kẻ IH vuông góc vs AB tại I, kẻ HK vuông góc vs AC tại K. Vẽ các điểm D và E sao cho I và K lần lượt là trung điểm của HD và HE. Chứng minh AEAH 4. Tam giác ADE là tam giác gì? Vì sao? 5. Chứng minh DE song song vs BC 6. Tam giác ABC cần thỏa mãn điều kiện gì để A là trung điểm của DE Giải giúp mình với cám ơn!!!
Đọc tiếp
Cho tam giác ABC có AB= AC =10cm, BC=12cm,kẻ AH vuông góc vs BC tại H 1. Chứng minh tam giác ABH=ACH và H là trung điểm của BC 2. Tính AH? 3. Kẻ IH vuông góc vs AB tại I, kẻ HK vuông góc vs AC tại K. Vẽ các điểm D và E sao cho I và K lần lượt là trung điểm của HD và HE. Chứng minh AE=AH 4. Tam giác ADE là tam giác gì? Vì sao? 5. Chứng minh DE song song vs BC 6. Tam giác ABC cần thỏa mãn điều kiện gì để A là trung điểm của DE Giải giúp mình với cám ơn!!!
1: Xét ΔABH vuông tại H và ΔACH vuông tại H có
AB=AC
AH chung
Do đó: ΔABH=ΔACH
Suy ra: BH=CH
hay H là trung điểm của BC
2: BH=CH=BC/2=6cm
=>AH=8cm
3: Xét ΔAHE có
AK là đường cao
AK là đường trung tuyến
Do đó:ΔAHE cân tại A
hay AH=AE(1)
4: Xét ΔADH có
AI là đường cao
AI là đường trung tuyến
Do đó:ΔADH cân tại A
=>AD=AH(2)
Từ (1) và (2)suy ra AD=AE
hay ΔADE cân tại A
Đúng 0
Bình luận (0)
cho tam giác ABC vuông tại A . Kẻ AH vuông góc vs BC (H thuộc BC) . Tia phân giác của góc HAC cắt BC tại D. CMR: tam giác ABD là tam giác cân
chị tự kẻ hình :
AH _|_ BC (gt) => góc DHA = 90o (đn)
=> góc ADH + góc DHA + góc DAH = 180 (đl)
=> góc ADH + 90 + góc DAH = 180
=> góc ADH = 180 - 90 - góc DAH
=> góc ADH = 90 - góc DAH (1)
có tam giác ABC vuông tại A (gt)
=> góc DAB + góc CAD = 90
=> góc DAB = 90 - góc CAD (2)
AD là phân giác của góc HAC (gt) => góc CAD = góc DAH (đn) (3)
(1)(2)(3) => góc DAB = góc ADB
=> tam giác ABD cân tại B (dh)
Đúng 1
Bình luận (0)
cho tam giác ABC vuông tại A kẻ AH vuông góc vs BC ( H thuộc BC ) Ah là pg của góa A , góc BK là pg của góc B ( K thuộc AC ) Gọi I là giao điểm AH và BK . Chứng minh :
a) Góc AIK = BAH + KBC
b) AIK = AKI
a: \(\widehat{AIK}=180^0-\widehat{HAC}-\widehat{AKB}\)
\(=90^0-\widehat{HAC}+90^0-\widehat{AKB}\)
\(=\widehat{ABK}+\widehat{C}=\widehat{KBC}+\widehat{BAH}\)
b: \(\widehat{AKI}=90^0-\widehat{ABK}\)
\(\widehat{AIK}=\widehat{BIH}=90^0-\widehat{KBC}\)
mà \(\widehat{ABK}=\widehat{KBC}\)
nên \(\widehat{AKI}=\widehat{AIK}\)
Đúng 0
Bình luận (0)