\(\frac{1}{2}\)- 0, 03 =

Những câu hỏi liên quan
Cho A=\(\frac{1}{1^2}+\frac{1}{2^2}+\frac{1}{3^2}+...+\frac{1}{50^2}\)
Chứng minh A < 2.
12 phút trước (19:03)
Hãy biểu diễn các điểm sau trên mặt phảng tọa độ Oxy:
M (\(-\frac{1}{3}\) ;1) ; N (2 ;-1) ' P(0; 3) ; Q(-3 ; 0)
Chỉ giùm
a) Đọc nội dung sau và thảo luận với bạn:Nhận xét: Trong một phép chia, số chia luôn phải khác 0.b) Tính nhẩm:0 : 70 : 90 : 50 : 40 : 100 : 1c) Tìm phép tính sai rồi sửa lại cho đúng:8 : 8 18 : 1 10 × 2 02 : 0 03 × 0 03 : 0 0
Đọc tiếp
a) Đọc nội dung sau và thảo luận với bạn:
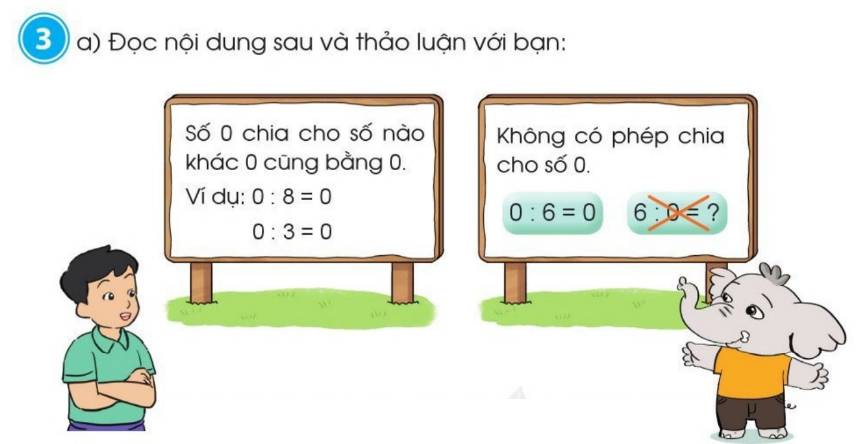
Nhận xét: Trong một phép chia, số chia luôn phải khác 0.
b) Tính nhẩm:
0 : 7 0 : 9 | 0 : 5 0 : 4 | 0 : 10 0 : 1 |
c) Tìm phép tính sai rồi sửa lại cho đúng:
8 : 8 = 1 8 : 1 = 1 | 0 × 2 = 0 2 : 0 = 0 | 3 × 0 = 0 3 : 0 = 0 |
a) Học sinh thực hành.
b)
0 : 7 = 0 0 : 9 = 0 | 0 : 5 = 0 0 : 4 = 0 | 0 : 10 = 0 0 : 1 = 0 |
c) Các phép tính sai là:
8 : 1 = 1. Sửa: 8 : 1 = 8.
2 : 0 = 0. Sửa: 0 : 2 = 0.
3 : 0 = 0. Sửa: 0 : 3 = 0.
Đúng 0
Bình luận (0)
Giải các phương trình sau: 1) 4x - 9 = 0 2) - 2x + 50 = 03) 3x + 11 = 0
1) (3x - 2)(4x + 5) = 0
2) (4x + 2)(x2 + 3) = 0
3) (2x + 7)(x - 3)(5x - 1) = 0
4) x2 - 3x = 0
5) x2 - x = 0
1
(3x-2)(4x+5)=0
⇔ 3x-2=0 -> x= 2/3
⇔ 4x-5=0 x= 5/4
Vậy tập nghiệm S = { 2/3; 5/4}
Đúng 1
Bình luận (0)
2, (4x+2)(\(X^2\)+3)=0
⇔ 4x+2=0 -> x= -1/2
\(x^2\)+3=0 -> x= \(\sqrt{3}\); -\(\sqrt{3}\)
Vaayj tập nghiệm S= { -1/2; \(\sqrt{3}\);-\(\sqrt{3}\)}
Đúng 1
Bình luận (0)
3)
(2x+7)(x-3)(5x-1)=0
⇔ 2x+7=0 -> x= -7/2
x-3 =0 -> x = 3
5x-1 =0 -> x= 1/5
Vậy tập nghiệm S={ -7/2; 3; 1/5}
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Tìm x biết
1.x(x+1)-x2+1=0
2.4x.(x-2)-6+3x=0
3.x(x+2)-3(x+2)=0
1. x(x + 1) - x2 + 1 = 0
<=> x(x + 1) - (x2 - 1) = 0
<=> x(x + 1) - (x + 1)(x - 1) = 0
<=> (x - x + 1)(x + 1) = 0
<=> x + 1 = 0\
<=> x = -1
2. 4x(x - 2) - 6 + 3x = 0
<=> 4x(x - 2) - (3x - 6) = 0
<=> 4x(x - 2) - 3(x - 2) = 0
<=> (4x - 3)(x - 2) = 0
<=> \(\left[{}\begin{matrix}4x-3=0\\x-2=0\end{matrix}\right.\)
<=> \(\left[{}\begin{matrix}x=\dfrac{3}{4}\\x=2\end{matrix}\right.\)
3. x(x + 2) - 3(x + 2) = 0
<=> (x - 3)(x + 2) = 0
<=> \(\left[{}\begin{matrix}x-3=0\\x+2=0\end{matrix}\right.\)
<=> \(\left[{}\begin{matrix}x=3\\x=-2\end{matrix}\right.\)
Đúng 0
Bình luận (0)
 một khối gỗ có dạng hình hộp chữ nhật được cắt đi 1 phần như hình vẽ. tính thể tích của phần bị cắt
một khối gỗ có dạng hình hộp chữ nhật được cắt đi 1 phần như hình vẽ. tính thể tích của phần bị cắt
hinh ve ???
1.Giải phương trình:
3x^4+x^2-4=03\(x^4\) +\(x^2\) - 4=0
\dfrac{4}{5}
\(3x^4+x^2-4=0\)
\(\Leftrightarrow3x^4-3x^2+4x^2-4=0\)
\(\Leftrightarrow3x^2\cdot\left(x^2-1\right)+4\cdot\left(x^2-1\right)=0\)
\(\Leftrightarrow\left(x^2-1\right)\left(3x^2+4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2-1=0\\3x^2+4=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\pm1\\x^2=-\dfrac{4}{3}\left(l\right)\end{matrix}\right.\)
\(S=\left\{\pm1\right\}\)
Đúng 1
Bình luận (0)
Đặt `x^2=t(t>=0)`
Ta có PT: `3t^2+t-4=0`
`3+1-4=0`
`=> t_1 = 1 ; t_2 = -4/3 (L)`
`=> x^2=1`
`<=> x=\pm 1`
Vậy `S={\pm 1}`.
Đúng 1
Bình luận (0)
\(3x^4+x^2-4=0\\ \Leftrightarrow3x^4-3x^2+4x^2-4=0\\ \Leftrightarrow3x^2\left(x^2-1\right)+4\left(x^2-1\right)=0\\ \Leftrightarrow\left(x-1\right)\left(x+1\right)\left(3x^2+4\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=1\\x=-1\\3x^2+4>0\forall x\end{matrix}\right.\)
Vậy \(S=\left\{-1;1\right\}\) là tập nghiệm của pt
Đúng 1
Bình luận (0)
1) cosx\(^2\)+sinx=0
2) 2cos\(^2\)x-cos2x+cosx=0
3) sin\(^2\)x-3cos2x-2=0
4) tanx+\(\dfrac{2}{cotx}\)=0
3.
\(\dfrac{1}{2}-\dfrac{1}{2}cos2x-3cos2x-2=0\)
\(\Leftrightarrow-7cos2x-3=0\)
\(\Rightarrow cos2x=-\dfrac{3}{7}\)
\(\Rightarrow2x=\pm arccos\left(-\dfrac{3}{7}\right)+k2\pi\)
\(\Rightarrow x=\pm\dfrac{1}{2}arccos\left(-\dfrac{3}{7}\right)+k\pi\)
4.
ĐKXĐ: \(x\ne\dfrac{k\pi}{2}\)
\(tanx+2tanx=0\)
\(\Rightarrow3tanx=0\)
\(\Rightarrow tanx=0\)
\(\Rightarrow x=k\pi\) (loại do ĐKXĐ)
Vậy pt đã cho vô nghiệm
Đúng 2
Bình luận (0)
1.
\(\Leftrightarrow1-sin^2x+sinx=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=\dfrac{1+\sqrt{5}}{2}>1\left(loại\right)\\sinx=\dfrac{1-\sqrt{5}}{2}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=arcsin\left(\dfrac{1-\sqrt{5}}{2}\right)+k2\pi\\x=\pi-arcsin\left(\dfrac{1-\sqrt{5}}{2}\right)+k2\pi\end{matrix}\right.\) (\(k\in Z\))
2.
\(2cos^2x-\left(2cos^2x-1\right)+cosx=0\)
\(\Leftrightarrow cosx+1=0\)
\(\Leftrightarrow cosx=-1\)
\(\Leftrightarrow x=\pi+k2\pi\) (\(k\in Z\))
Đúng 1
Bình luận (0)

























