Cho tam giác ABC nội tiếp đường trong tam O với AB # AC . Đường cao AH trung tuyến AM phân giác AD gọi E là giao điểm của AD với đường tròn chứng minh O,M,E thẳng hàng . Giả sử góc A< 90 chứng minh góc DAM nhỏ hơn góc DAH

Những câu hỏi liên quan
Cho tam giác ABC cân tại A, đ tròn (O) ngoại tiếp tam giác ABC, đường tròn tâm (O') tiếp xúc trong với (O) và tiếp xúc với cạnh AB ở P, AC ở Q. Cm trung điểm I của PQ là tâm đ tròn nội tiếp tam giác ABC
Cho tam giác ABC có ba góc nhọn và ABAC. Tam giác ABC nội tiếp đường tròn (O;R). Đường cao AH của tam giác ABC cắt đường tròn (O;R) tại điểm thứ hai là D. Kẻ DM vuông góc với AB tại M.a) Chứng minh tứ giác BDHM nội tiếp đường tròn.b) Chứng minh DA là tia phân giác của widehat{MDC}c) Gọi N là hình chiếu vuông góc của D lên đường thẳng AC, chứng minh ba điểm M, H, N thẳng hàng.d) Chứng minh AB^2+AC^2+CD^2+BD^28R^2
Đọc tiếp
Cho tam giác ABC có ba góc nhọn và AB>AC. Tam giác ABC nội tiếp đường tròn (O;R). Đường cao AH của tam giác ABC cắt đường tròn (O;R) tại điểm thứ hai là D. Kẻ DM vuông góc với AB tại M.
a) Chứng minh tứ giác BDHM nội tiếp đường tròn.
b) Chứng minh DA là tia phân giác của \(\widehat{MDC}\)
c) Gọi N là hình chiếu vuông góc của D lên đường thẳng AC, chứng minh ba điểm M, H, N thẳng hàng.
d) Chứng minh \(AB^2+AC^2+CD^2+BD^2=8R^2\)
a: góc BHD+góc BMD=180 độ
=>BHDM nội tiếp
b: BHDM nội tiếp
=>góc HDM+góc HBM=180 độ
=>góc ADM=góc ABC
=>góc ADM=góc ADC
=>DA là phân giáccủa góc MDC
c: Xét tứ giác DHNC có
góc DHC=góc DNC=90 độ
=>DHNC nội tiếp
=>góc NHD=góc NDC
góc NHD+góc MHD
=180 độ-góc NCD+góc MBD
=180 độ+180 độ-góc ABD-góc ACD
=180 độ
=>M,H,N thẳng hàng
Đúng 0
Bình luận (0)
cho tam giác ABC nội tiếp đường tròn O,đường tròn K tiếp xúc trong vs đtròn O tại T và tiếp xúc 2 cạnh AB,AC tại E,F chưng minh tâm I đtròn nội tiếp tam giác ABC là trung điểm EF
Bổ sung: ΔABC cân tại A
ΔABC cân tại A
=>AO đi qua trug diểm I của EF
Vẽ IK vuông góc AB tại K, gọi H và G lần lượt là giao của OA với BC và(O)
Vì OE vuông góc AB, IK vuông goc AB, GB vuông góc AB
=>OE//IK//GB
ΔABG có IK//GB
nên IK/BG=AI/AG
=>IK=AI*BG/AG
ΔABH có EI//BH
ΔABE có OE//BG
=>IH/AH=BE/BA=OG/AG và AE/AB=AI/AH
=>IH=AH*OE/AE
ΔABG có OE//BG
nên AB/AE=BG/OE
AH/AI=AB/AE=BG/OE
=>AH*OE=AI*BG
=>AH*OG=AI*BG
=>IK=IH
=>ĐPCM
Đúng 0
Bình luận (1)
Cho tam giác ABC vuông tại A. Đường tròn (O) nội tiếp tam giác ABC tiếp xúc với AB, AC lần lượt tại D và E. Tính bán kính của đường tròn (O) biết AB = 3cm, AC = 4cm.
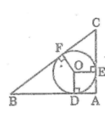
Áp dụng định lí Pitago vào tam giác vuông ABC ta có :
B C 2 = A B 2 + A C 2 = 3 2 + 4 2 = 25
Suy ra : BC = 5 (cm)
Theo tính chất hai tiếp tuyến giao nhau ta có:
AD = AE
BD = BF
CE = CF
Mà: AD = AB – BD
AE = AC – CF
Suy ra: AD + AE = AB – BD + (AC – CF)
= AB + AC – (BD + CF)
= AB + AC – (BF + CF)
= AB + AC – BC
Suy ra:
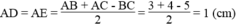
Đúng 0
Bình luận (0)
Cho tam giác ABC đều nội tiếp đường tròn (O;R). Vẽ đường tròn (I) tiếp xúc với AB, AC và tiép xúc trong với (O). Tính IB theo R
minh moi bn vao link nay dang ky roi tra loi minigame nha : https://alfazi.edu.vn/question/5b7768199c9d707fe5722878
Đúng 0
Bình luận (0)
Gọi tiếp điểm của đường tròn (I) với AB và (O;R) theo thứ tự là D và E.
Đường tròn (I) tiếp xúc trong với (O;R) tại E nên 4 điểm A;O;I;E thẳng hàng.
Ta có: AO là phân giác của ^BAC (Do \(\Delta\)ABC đều nội tiếp (O))
=> AI là phân giác ^BAC => ^DAI = ^BAC / 2 = 300
AB tiếp xúc với (I) tại D => ^ADI = 900.
Xét \(\Delta\)AID có: ^ADI = 900; ^DAI = 300 => \(\Delta\)AID nửa đều \(\Rightarrow\frac{ID}{AI}=\frac{1}{2}\)
Hay \(\frac{IE}{AI}=\frac{1}{2}\Rightarrow\frac{IE}{AE}=\frac{1}{3}\)(Do A;I;E thẳng hàng) \(\Rightarrow IE=ID=\frac{2R}{3}\)
Thấy ^ABE chắn nửa đg tròn (O;R) => ^ABE = 900 => BE vuông góc AB. Mà ID vuông góc AB
=> ID // BE => \(\frac{IE}{AE}=\frac{BD}{AB}=\frac{1}{3}\)(Theo ĐL Thales)
Áp dụng ĐL Pytagorean ta dễ dàng tính được: \(AB=R.\sqrt{3}\)\(\Rightarrow BD=\frac{AB}{3}=\frac{R}{\sqrt{3}}\)
Trong \(\Delta\)BDI có ^IDB = 900 . Áp dụng ĐL Pytagorean:
\(IB=\sqrt{BD^2+ID^2}=\sqrt{\frac{R^2}{3}+\frac{4R^2}{9}}=\sqrt{\frac{7R^2}{9}}=\frac{R.\sqrt{7}}{3}\)
ĐS: .....
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A.Đường tròn (O) nội tiếp tam giác ABC tiếp xúc với AB,AClần lượt tại D và E. Biết AB=3 cm,AC=4cTính bán kính đường tròn (O)
Cho tam giác D;E là tiếp điểm của đường tròn (O) nội tiếp tam giác với AB,AC, H là giao điểm của OB và DE.
a) Chứng minh rằng O,E,H,C cùng thuộc 1 đường tròn
b) Phân giác trong tam giác ABC, đường trung bình song song với AB và DE đồng quy.
Cho tam giác ABC (AB < AC) có ba góc nhọn nội tiếp trong đường tròn tâm O, bán kính R. Gọi H là giao điểm của ba đường cao AD, BE, CF của tam giác ABC.
1. Chứng minh rằng AEHF và AEDB là các tứ giác nội tiếp đường tròn.
2. Vẽ đường kính AK của đường tròn (O). Chứng minh tam giác ABD và tam giác AKC đồng dạng với nhau.
3. Chứng minh rằng OC vuông góc với DE.
ta có
\(\widehat{AEH}=90^0;\widehat{AFH}=90^0\)
=> \(\widehat{AEH}+\widehat{AFH}=180^0\)
=> tứ giác AEHF nội tiếp được nhé
ta lại có AEB=ADB=90 độ
=> E , D cùng nhìn cạnh AB dưới 1 góc zuông
=> tứ giác AEDB nội tiếp được nha
b)ta có góc ACK = 90 độ ( góc nội tiếp chắn nửa đường tròn)
hai tam giác zuông ADB zà ACK có
ABD = AKC ( góc nội tiếp chắn cung AC )
=> tam giác ABD ~ tam giác AKC (g.g)
c) zẽ tiếp tuyến xy tại C của (O)
ta có OC \(\perp\) Cx (1)
=> góc ABC = góc DEC
mà góc ABC = góc ACx
nên góc ACx= góc DEC
do đó Cx//DE ( 2)
từ 1 zà 2 suy ra \(OC\perp DE\)
Cho tam giác ABC nội tiếp đường tròn (O). Đường phân giác AD của tam giác ABC cắt cung BC ở E. Đường tròn (I) tiếp xúc trong với (O) và tiếp xúc với BC tại T cắt AD ở M, N (N nằm giữa A và M); CM cắt đường tròn (O) tại K. Vẽ dây KL//AB. Chứng minh rằng ba điểm C, N, L thẳng hàng.
CM được S,T,E thẳng hàng
Xét tam giác ECT zà tam giác EST có \(\widehat{CET}\left(chung\right),\widehat{ECT}=\widehat{ESC}\)
=>tam giác ECT=tam giác EST(g.g)
=>\(\frac{EC}{ES}=\frac{ET}{EC}=>ET.ES=EC^2\)
xét tam giác EMT zà tam giác ESN có \(\widehat{MET}\left(chung\right),\widehat{EMT}=\widehat{ESN}\)
=> tam giác ECT = tam giác ESN(g.g)
=>\(\frac{EM}{ES}=\frac{ET}{EN}=>ET.ES=EM.EN=EM.EN\\\)
Nên \(EC^2=EM.EN=\left(=ET.ES\right)=\frac{EC}{EN}=\frac{EM}{EC}\)
tam giác ECM = tam giasc ENC (c.g.c)
=>\(\widehat{EMC}=\widehat{ENC}\)
=>\(\widehat{ECD}+\widehat{DCM}=\widehat{NAC}+\widehat{NCA}\)
mà \(\widehat{ECD=\widehat{NAC}}\)
nên \(\widehat{DCM}=\widehat{NCA}\)
ta có \(KL//AB=>\widebat{BK}=\widebat{AL}=>\widehat{DCM}=\widehat{LCA}\)
ta có\(\widehat{NCA}=\widehat{LCA}\left(=\widehat{DCM}\right)\)
=> hai tia CN , CL trùng nhau .zậy C,N,L thẳng hàng
Cho tam giác ABC vuông tại A.Đường tròn (O) nội tiếp tam giác ABC tiếp xúc với AB,AC lần lượt tại D và E.
Biết AB=3,AC=4cm.Bán kính đường tròn (O) là ......cm
Ta có: AC = 5
Gọi bán kính đường tròn nội tiếp là r
Ta có:
S(ABC) =S(OAB) + S(OAC) +S(OBC) (1)
S(OAB) = r*AB/2
S(OAC) = r*AC/2
S(OBC) = r*BC/2
=> S(OAB) + S(OAC) +S(OBC) = r* (AB+BC+CA)/2 = 6r (2)
Mặt khác; S(ABC) = AB.AC/2 = 6 (3)
Từ (1), (2), (3) :
=> 6r = 6 => r = 1.
Ủng hộ mk nha!
Đúng 0
Bình luận (0)



















