(-6x^2y^3z).(5/18xy^2).(1/2z^2)

Những câu hỏi liên quan
BÀI 8: THU GỌN VÀ TÌM BẬC CỦA MỖI ĐA THỨC:
A= -2xy + 3/2xy^2 + 1/2xy^2 + xy
B= xy^2z + 2xy^2z - xyz - 3xy^2z + xy^2z
C= 4x^2y^3 + x^4 - 2x^2 + 6x^4 - x^2y^3
D= 3/4xy^2 - 2xy - 1/2xy^2 + 3xy
E= 2x^2 - 3y^3 - z^4 - 4x^2 + 2y^3 + 3z^4
F= 3xy^2z + xy^2z - xyz + 2xy^2z -3xyz
0,2:x=1,03+3,97
a: A=-2xy+xy+xy^2=-xy+xy^2
Bậc là 3
b: \(B=xy^2z+2xy^2z-3xy^2z+xy^2z-xyz=-xyz+xy^2z\)
Bậc là 4
c: \(C=4x^2y^3-x^2y^3+x^4+6x^4-2x^2=3x^2y^3+7x^4-2x^2\)
Bậc là 5
d: \(D=\dfrac{3}{4}xy^2-\dfrac{1}{2}xy^2+xy=\dfrac{1}{4}xy^2+xy\)
bậc là 3
e: \(E=2x^2-4x^2+3z^4-z^4-3y^3+2y^3\)
=-2x^2+2z^4-y^3
Bậc là 4
f: \(=3xy^2z+xy^2z+2xy^2z-4xyz=6xy^2z-4xyz\)
Bậc là 4
Đúng 0
Bình luận (0)
Giải hệ phương trình
2
x
-
3
y
+
z
-
7...
Đọc tiếp
Giải hệ phương trình 2 x - 3 y + z = - 7 - 4 x + 5 y + 3 z = 6 x + 2 y - 2 z = 5
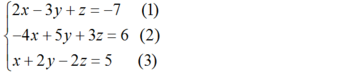
Đưa hệ phương trình về hệ dạng tam giác bằng cách khử dần các ẩn.
Nhân phương trình (1) với 2 rồi cộng với phương trình (2) và nhân phương trình (3) với 4 rồi cộng với phương trình (2) ta được:
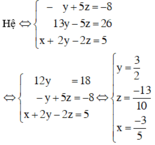
Vậy hệ phương trình có nghiệm 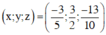
Đúng 0
Bình luận (0)
a(15 xy^2z^3 :(3xyz^2)
b(12 x^y^4 : (-4x^4y^2)
c (-15x^2y^3z^2 ) :(-6xz^2)
d(x-y)^5 : (y-x)^3
(x-y)^5 : (y-x)^2
f(3xy-6x)^3 : 9(2x-y)
a: \(15xy^2z^3:3xyz^2=5yz\)
b: \(12x^4y^4:\left(-4x^4y^2\right)=-3y^2\)
c: \(\dfrac{-15x^2y^3z^2}{-6xz^2}=\dfrac{5}{2}xy^3\)
d: \(\dfrac{\left(x-y\right)^5}{\left(y-x\right)^3}=-\left(x-y\right)^2\)
Đúng 1
Bình luận (1)
tìm x,y,z trong moi truong hop
a,(6x+1)2020 +(3y+1)2020 +|x+y+2z2 |=0
b, \(\frac{3x-2y}{5}=\frac{2z-5x}{3}=\frac{5y-3z}{2}\) và x+y+z=-50
Cho x,y,z>=0 và x+y+z=1. Tìm MaxP=(x+2y+3z)(6x+3y+2z)
\(P=\dfrac{1}{2}\left(2x+4y+6z\right)\left(6x+3y+2z\right)\le\dfrac{1}{8}\left(2x+4y+6z+6x+3y+2z\right)^2\)
\(P\le\dfrac{1}{8}\left(8x+7y+8z\right)^2\le\dfrac{1}{8}\left(8x+8y+8z\right)^2=8\)
\(P_{max}=8\) khi \(\left\{{}\begin{matrix}x+y+z=1\\7y=8y\\2x+4y+6z=6x+3y+2z\end{matrix}\right.\) \(\Leftrightarrow\left(x;y;z\right)=\left(\dfrac{1}{2};0;\dfrac{1}{2}\right)\)
Đúng 2
Bình luận (0)
Tim Max P=(x+2y+3z)(6x+3y+2z)
biết x+y+z=1
cho các đơn thức 7/12x^2-y^2z-x^2y^3z^2;-5/4x^2y^2
Viết phương trình mặt phẳng song song với (P): 6x -2y + 3z + 7 0 và tiếp xúc với mặt cầu
x
2
+
y
2
+
z
2
+2x+2y+2z - 1 0 A. 6x - 2y + 3z - 8 0 B. 6x - 2y + 3z - 3 0 C. 6x - 2y + 3z -7 0 D. 6x - 2y + 3z - 5 0
Đọc tiếp
Viết phương trình mặt phẳng song song với (P): 6x -2y + 3z + 7 = 0 và tiếp xúc với mặt cầu x 2 + y 2 + z 2 +2x+2y+2z - 1 = 0
A. 6x - 2y + 3z - 8 = 0
B. 6x - 2y + 3z - 3 = 0
C. 6x - 2y + 3z -7 = 0
D. 6x - 2y + 3z - 5 = 0
Chọn C
Gọi (Q) là mặt phẳng cần tìm. Vì (Q) song song với (P) nên phương trình (Q) có dạng
6x - 2y + 3z + a = 0
Tâm mặt cầu I(-1;-1;-1) bán kính R = 2
Vì (Q) tiếp xúc với mặt cầu nên d(I,(Q))=R hay
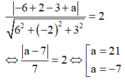
Đúng 0
Bình luận (0)
Viết phương trình mặt phẳng song song với
P
:
6
x
-
2
y
+
3
z
+
7
0
và tiếp xúc với mặt cầu
x
2
+
y
2
+
z
2
+
2
x
+
2
y
+
2
z
-
1...
Đọc tiếp
Viết phương trình mặt phẳng song song với P : 6 x - 2 y + 3 z + 7 = 0 và tiếp xúc với mặt cầu x 2 + y 2 + z 2 + 2 x + 2 y + 2 z - 1 = 0
A. 6 x - 2 y + 3 z - 8 = 0
B. 6 x - 2 y + 3 z - 3 = 0
C. 6 x - 2 y + 3 z - 7 = 0
D. 6 x - 2 y + 3 z - 5 = 0
Đáp án C
Gọi (Q) là mặt phẳng cần tìm. Vì (Q) song song với (P) nên phương trình (Q) có dạng
![]()
Tâm mặt cầu I(-1;-1;-1) bán kính R = 2
Vì (Q) tiếp xúc với mặt cầu nên d(I,(Q)) = R hay
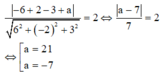
Đúng 0
Bình luận (0)













