tìm x sao cho x^2(x-3)(x+5)>0

Những câu hỏi liên quan
1, tìm x biết :
[ x-3 ] + [ x-2 ] + [ x-1 ] + ... + [ x+5 ] = 0
2, tìm x sao cho :
[ x-7 ] . [ x+3 ] < 0
3, cho biểu thức : A = [ 5.x^2 - 8.x^2 - 9.x^2 ] . [ 3y^3] . tìm x, y để A > hoặc = 0
cậu chia từng câu ra cho mình nhé
Đúng 0
Bình luận (0)
tìm số hữu tỉ x sao cho
a)(x- 2/5).(x+3/7)>0
b) (x-2/5).(x+3/7).(x+3/4)>0
c)(2/3.x-1/5).(3/5.x+2/3)<0
tìm số hữu tỉ x sao cho
a)(x- 2/5).(x+3/7)>0
b) (x-2/5).(x+3/7).(x+3/4)>0
c)(2/3.x-1/5).(3/5.x+2/3)<0
Giúp mình với
Bài 11: Cho biểu thức A = \(\dfrac{9-3x}{x^2+4x-5}-\dfrac{x+5}{1-x}-\dfrac{x+1}{x+5}\) (với x ≠ -5; x ≠ 1)
a) Rút gọn A b) Tìm các giá trị nguyên của x để A nhận giá trị nguyên
c) Tìm x sao cho A<0 d) Tìm x sao cho |A| = 3
\(a,A=\dfrac{9-3x+x^2+10x+25-x^2+1}{\left(x-1\right)\left(x+5\right)}\\ A=\dfrac{7x+35}{\left(x-1\right)\left(x+5\right)}=\dfrac{7\left(x+5\right)}{\left(x-1\right)\left(x+5\right)}=\dfrac{7}{x-1}\\ b,A\in Z\\ \Leftrightarrow x-1\inƯ\left(7\right)=\left\{-7;-1;1;7\right\}\\ \Leftrightarrow x\in\left\{-6;0;2;8\right\}\left(tm\right)\\ b,A< 0\Leftrightarrow x-1< 0\left(7>0\right)\\ \Leftrightarrow x< 1;x\ne-5\\ c,\left|A\right|=3\Leftrightarrow\dfrac{7}{\left|x-1\right|}=3\Leftrightarrow\left|x-1\right|=\dfrac{7}{3}\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{7}{3}+1=\dfrac{10}{3}\left(tm\right)\\x=-\dfrac{7}{3}+1=-\dfrac{4}{3}\left(tm\right)\end{matrix}\right.\)
Đúng 2
Bình luận (0)
tìm x thuộc z sao cho
(x-5) (x+2)<0
(x-3) (x+2)>0
a. (x - 5).(x + 2) < 0
Vì x - 5 < x + 2 nên xét trường hợp:
x - 5 < 0; x + 2 > 0
=> x < 5; x > -2
=> -2 < x < 5
=> x thuộc {-1; 0; 1; 2; 3; 4}
b. (x - 3) . (x + 2) > 0
+) x - 3 < 0; x + 2 < 0
=> x < 3; x < -2
=> x -2 thì thỏa mãn
+) x - 3 > 0; x + 2 > 0
=> x > 3; x > -2
=> x > 3 là thỏa mãn.
Đúng 0
Bình luận (0)
hic quên cách làm rùi để mk tìm lại
Đúng 0
Bình luận (0)
tìm x thuộc z sao cho
a/ (x2+1).(x+3)=0
b/(x+2).(x-1)<0
c/(x2+3).(x-4)>0
d/(x+5).(x-7)>0
a) Ta có : (x2 + 1).(x + 3) = 0
\(\Leftrightarrow\orbr{\begin{cases}x^2+1=0\\x+3=0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x^2=-1\left(\text{loại}\right)\\x=-3\end{cases}}\)
Đúng 0
Bình luận (0)
B=\(\dfrac{1}{x}\)+\(\dfrac{1}{x+5}\)+\(\dfrac{x-5}{x\left(x+5\right)}\)
1) rút gọn B.
2) tìm x để B > 0 .
3) tìm x sao cho B nhận giá trị nguyên.
a)B=x+5 +x +x-5/x(x-5)=3x/x(x-5)=3/x-5
b)đkxđ x khác 5
Đúng 0
Bình luận (0)
a)B=x+5 +x +x-5/x(x-5)=3x/x(x-5)=3/x-5
b)đkxđ x khác 5
Đúng 0
Bình luận (0)
1, đk x khác 0 ; -5
\(B=\dfrac{x+5+x+x-5}{x\left(x+5\right)}=\dfrac{3}{x+5}\)
2, B = 3/(x+5) > 0 => x + 5 > 0 <=> x > -5
3, \(\Rightarrow x+5\inƯ\left(3\right)=\left\{\pm1;\pm3\right\}\)
| x + 5 | 1 | -1 | 3 | -3 |
| x | -4 | -6 | -2 | -8 |
Đúng 1
Bình luận (0)
Tìm x sao cho :
a. (x -2)^2 . (x + 1) . (x - 4) < 0
b. [x^2 . (x - 3)] : (x - 9) < 0
c. 5/x < 1
a; (\(x\) - 2)2.(\(x+1\)).(\(x\) - 4) < 0
(\(x-2\))2 ≥ 0 ∀\(x\); \(x+1\) = 0 ⇒ \(x=-1\); \(x-4\) = 0 ⇒ \(x=4\)
Lập bảng ta có:
| \(x\) | - 1 4 |
| \(x+1\) | - 0 + | + |
| \(x-4\) | - | - 0 + |
| (\(x-2\))2 | + | + | + |
| (\(x-2\))2.(\(x+1\)).(\(x+4\)) | + 0 - 0 + |
Theo bảng trên ta có: -1 < \(x\) < 4
Vậy \(-1< x< 4\)
Đúng 0
Bình luận (0)
b; [\(x^2\).(\(x-3\)):(\(x-9\))] < 0
\(x-3=0\)⇒ \(x=3\); \(x-9\) = 0 ⇒ \(x=9\)
Lập bảng ta có:
| \(x\) | 3 9 |
| \(x-3\) | - 0 + | + |
| \(x-9\) | - | - 0 + |
| \(x^2\) | + | + | + |
| \(x^2\)(\(x-3\)):(\(x-9\)) | + 0 - 0 + |
Theo bảng trên ta có: 3 < \(x\) < 9
Vậy 3 < \(x\) < 9
Đúng 0
Bình luận (0)
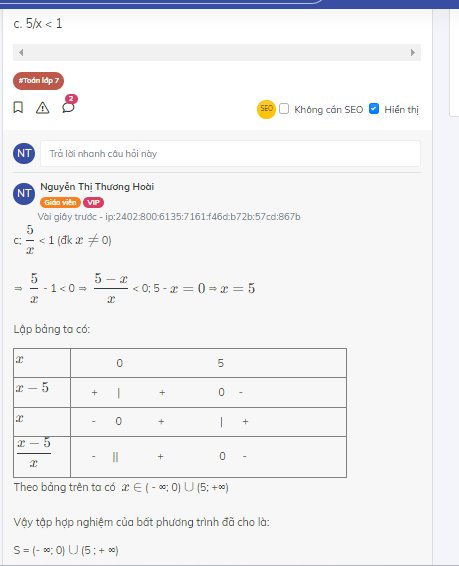
c; \(\dfrac{5}{x}\) < 1 (đk \(x\ne\) 0)
⇒ \(\dfrac{5}{x}\) - 1 < 0 ⇒ \(\dfrac{5-x}{x}\) < 0; 5 - \(x=0\) ⇒ \(x=5\)
Lập bảng ta có:
| \(x\) | 0 5 |
| \(x-5\) | + | + 0 - |
| \(x\) | - 0 + | + |
| \(\dfrac{x-5}{x}\) | - || + 0 - |
Theo bảng trên ta có \(x\) \(\in\) ( - ∞; 0) \(\cup\) (5; +∞)
Vậy tập hợp nghiệm của bất phương trình đã cho là:
S = (- ∞; 0) \(\cup\) (5 ; + ∞)
Đúng 0
Bình luận (0)
Tìm x sao cho :
a. (x -2)^2 . (x + 1) . (x - 4) < 0
b. [x^2 . (x - 3)] : (x - 9) < 0
c. 5/x < 1
a; (\(x\) - 2)2.(\(x+1\)).(\(x\) - 4) < 0
(\(x-2\))2 ≥ 0 ∀\(x\); \(x+1\) = 0 ⇒ \(x=-1\); \(x-4\) = 0 ⇒ \(x=4\)
Lập bảng ta có:
| \(x\) | - 1 4 |
| \(x+1\) | - 0 + | + |
| \(x-4\) | - | - 0 + |
| (\(x-2\))2 | + | + | + |
| (\(x-2\))2.(\(x+1\)).(\(x+4\)) | + 0 - 0 + |
Theo bảng trên ta có: -1 < \(x\) < 4
Vậy \(-1< x< 4\)
Đúng 0
Bình luận (0)
b; [\(x^2\).(\(x-3\)):(\(x-9\))] < 0
\(x-3=0\)⇒ \(x=3\); \(x-9\) = 0 ⇒ \(x=9\)
Lập bảng ta có:
| \(x\) | 3 9 |
| \(x-3\) | - 0 + | + |
| \(x-9\) | - | - 0 + |
| \(x^2\) | + | + | + |
| \(x^2\)(\(x-3\)):(\(x-9\)) | + 0 - 0 + |
Theo bảng trên ta có: 3 < \(x\) < 9
Vậy 3 < \(x\) < 9
Đúng 0
Bình luận (0)