Bài 3 (1 điểm) : Chứng minh rằng nếu 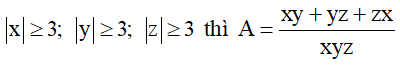
Chứng minh rằng nếu : |x| ≥ 3 ; |y| ≥ 3 ; |z| ≥ 3 thì \(A = \dfrac{xy+yz+zx}{xyz} \) có giá trị nhỏ hơn hoặc bằng 1 .
\(\left\{{}\begin{matrix}\left|x\right|\ge3\\\left|y\right|\ge3\\\left|z\right|\ge3\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}\left|\dfrac{1}{x}\right|\le\dfrac{1}{3}\\\left|\dfrac{1}{y}\right|\le\dfrac{1}{3}\\\left|\dfrac{1}{z}\right|\le\dfrac{1}{3}\end{matrix}\right.\)
\(\left|A\right|=\left|\dfrac{xy+yz+xz}{xyz}\right|=\left|\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}\right|\le\left|\dfrac{1}{x}\right|+\left|\dfrac{1}{y}\right|+\left|\dfrac{1}{z}\right|\le\dfrac{1}{3}+\dfrac{1}{3}+\dfrac{1}{3}=1\)
\(\Rightarrow A\le\left|A\right|\le1\) (đpcm)
Dấu "=" xảy ra khi \(x=y=z=3\)
Tìm x biết giá trị tuyệt đối của 3/2x+ giá trị tuyệt đối của 5/7y-1/2 nhỏ hơn hoặc bằng 0
2)chứng minh rằng 81^10-27^13-9^21 chia hết cho 225Giúp đi mình tick cho
2)81^10-27^13-9^21=3^40-3^39-3^42=3^39(3-1-3^3) =3^39.(-25)=3^37.9.(-25)=3^37.(-225) chia hết cho 225
Trong tam giác đều có cạnh bằng 2, ta đặt 33 điểm phân biệt (kể cả trên các cạnh). Chứng minh rằng tồn tại 3 điểm mà khoảng cách giữa 2 điểm trong 3 điểm đó nhỏ hơn hoặc bằng 1 2
Cho 2019 điểm trong đó cứ 3 điểm tạo thành một tam giác có diện tích không vượt quá 1.Chứng minh rằng 2019 điểm đó cùng nằm trong tam giác có diện tích nhỏ hơn hoặc bằng 4.
bài 1 Chứng minh rằng
Nếu a,b,c lớn hơn hoặc bằng 0 thì a3+b3+c3 lớn hơn hoặc bằng 3abc
bài 2 chứng minh rằng
Nếu a2+b2+c2=ab+ac+bc thì a=b=c
ai lam dc bai nay k giup minh voi
a2+b2+c2=ab+ac+bc
<=>2a2+2b2+2c2=2ab+2ac+2bc
<=>a2-2ab+b2+a2-2ac+c2+b2-2bc=0
<=>(a-b)2+(a-c)2+(b-c)2=0
<=>a-b=0 và a-c=0 và b-c=0
<=>a=b=c
cho f(x)=x2 +ax+b. chứng minh rằng với mọi giá trị của a,b thì trong 3 số | f(0) |, | f(x) | , | f(-1)| có ít nhất 1 số lớn hơn hoặc bằng 1/2
Tl
Bạn T i k 3 lần cho mình mình trả lời cho
#Kirito
a,Chứng tỏ rằng a^2 lớn hơn a;-a^2 nhỏ hơn hoặc bằng 0
b,Tìm giá trị nhỏ nhất của biểu thức (a-1)^2+2009
bài 1 Chứng minh rằng
Nếu a,b,c lớn hơn hoặc bằng 0 thì a3+b3+c3 lớn hơn hoặc bằng 3abc
bài 2 chứng minh rằng
Nếu a2+b2+c2=ab+ac+bc thì a=b=c
ai làm được 2 bài này thánh luôn
đố đó. đúng có thưởng. may ban thánh đâu có làm đc k. kho lam nen dung co
1 tìm giá trị của x để 5-2x nhỏ hơn 3+x
2 chứng minh rằng: a bình+b bình+2> hoặc = 2(a+b)
1)
Ta có : \(5-2x< 3+x\)
\(\Leftrightarrow-2x-x< 3-5\)
\(\Leftrightarrow-3x< -2\)
\(\Leftrightarrow x>\frac{2}{3}\)
Vậy bất phương trình có tập nghiệm \(\left\{x/x>\frac{2}{3}\right\}\)
2)
Ta có : \(a^2+b^2+2-2\left(a+b\right)\)
\(=a^2+b^2+2-2a-2b\)
\(=\left(a^2-2a+1\right)+\left(b^2-2b+1\right)\)
\(=\left(a-1\right)^2+\left(b-1\right)^2\)
Mà : \(\left(a-1\right)^2\ge0\forall a\)
\(\left(b-1\right)^2\ge0\forall b\)
\(\Rightarrow\left(a-1\right)^2+\left(b-1\right)^2\ge0\forall a;b\) ( luôn đúng )
\(\Rightarrow a^2+b^2+2\ge2\left(a+b\right)\left(đpcm\right)\)
Vậy \(a^2+b^2+2\ge2\left(a+b\right)\)