giúp mình vs giảng giúp mình cách đặt ẩn phụ
đốt cháy m (g) hh CH4, C2H4 trong khí O2 thu đc 0,4 mol CO2 và 0,6 mol H2O . tính giá trị m theo 4 cách
note : mình đã lm đc cách là đặt ẩn phụ rồi nhé , các bạn lm giúp mk 3 cách còn lại vs
C1:
Bảo toàn C: nC = 0,4 (mol)
Bảo toàn H: nH = 1,2 (mol)
=> mhh = 12.0,4 + 1.1,2 = 6(g)
C2:
Bảo toàn O: nO2 = \(\dfrac{0,4.2+0,6}{2}=0,7\left(mol\right)\)
Theo ĐLBTKL: mhh + mO2 = mCO2 + mH2O
=> mhh = 0,4.44 + 0,6.18 - 0,7.32 = 6(g)
C3:
Gọi công thức chung của hh là CxH4
PTHH: CxH4 + (x+1)O2 --to--> xCO2 + 2H2O
a------------------------>ax----->2a
=> \(\left\{{}\begin{matrix}ax=0,4\\2a=0,6\end{matrix}\right.\)
=> \(\left\{{}\begin{matrix}a=0,3\\x=\dfrac{4}{3}=>CTHH:C_{\dfrac{4}{3}}H_4\end{matrix}\right.\)
=> \(m_{hh}=0,3.20=6\left(g\right)\)
-giải phương trình
4(2x+7)-9(x+3)^2=0
- phân tích đa thức thành nhân tử bằng cách đặt ẩn phụ
(x^2+x+1)*(x^2+x+2)-12
(mọi người giải giúp mình vs ạ)
Bài 1 :
Mình nghĩ phải sửa đề ntn :
\(4\left(2x+7\right)^2-9\left(x+3\right)^2=0\)
\(\Leftrightarrow\left[2\left(2x+7\right)\right]^2-\left[3\left(x+3\right)\right]^2=0\)
\(\Leftrightarrow\left[2\left(2x+7\right)-3\left(x+3\right)\right]\left[2\left(2x+7\right)+3\left(x+3\right)\right]=0\)
\(\Leftrightarrow\left(4x+14-3x-9\right)\left(4x+14+3x+9\right)=0\)
\(\Leftrightarrow\left(x+5\right)\left(7x+23\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x+5=0\\7x+23=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=-5\\x=\frac{-23}{7}\end{cases}}}\)
Vậy....
b) \(A=\left(x^2+x+1\right)\left(x^2+x+2\right)-12\)
Đặt \(q=x^2+x+1\)ta có :
\(A=q\left(q+1\right)-12\)
\(A=q^2+q-12\)
\(A=q^2+4q-3q-12\)
\(A=q\left(q+4\right)-3\left(q+4\right)\)
\(A=\left(q+4\right)\left(q-3\right)\)
Thay \(q=x^2+x+1\)ta có :
\(A=\left(x^2+x+1+4\right)\left(x^2+x+1-3\right)\)
\(A=\left(x^2+x+5\right)\left(x^2+x-2\right)\)
\(A=\left(x^2+x+5\right)\left(x^2+2x-x-2\right)\)
\(A=\left(x^2+x+5\right)\left[x\left(x+2\right)-\left(x+2\right)\right]\)
\(A=\left(x^2+x+5\right)\left(x+2\right)\left(x-1\right)\)
Cách 2 của câu 2:
Đặt \(x^2+x+2=t\)
Ta có: \(A=\left(x^2+x+1\right)\left(x^2+x+2\right)-12\)
\(=t\left(t-1\right)-12=t^2-t-12\)
\(=\left(t-4\right)\left(t+3\right)=\left(x^2+x-2\right)\left(x^2+x+5\right)\)
\(=\left(x-1\right)\left(x+2\right)\left(x^2+x+5\right)\)
giải phương trình bằng cách đặt ẩn phụ
\(x^2+\sqrt[3]{x^4-x^2}=2x+1\)
giúp mình với
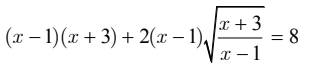 ( bài này giải theo phương pháp đặt ẩn phụ đúng không mọi người ? giải giúp mình với
( bài này giải theo phương pháp đặt ẩn phụ đúng không mọi người ? giải giúp mình với
đkxđ: \(\dfrac{x+3}{x-1}\ge0\)
Ptr ⇔\(\left(x-1\right)\left(x+3\right)+\dfrac{2\left(x-1\right)\sqrt{\left(x+3\right)\left(x-1\right)}}{x-1}=8\\ \Leftrightarrow\left(x-1\right)\left(x+3\right)+2\sqrt{\left(x-1\right)\left(x+3\right)}-8=0\)
Đặt \(\sqrt{\left(x-1\right)\left(x+3\right)}=a\) (a≥0)
Ptr ⇔ \(a^2+2a-8=0\)
⇔a=2 (tm) hoặc a=-4 (loại)
⇒\(\sqrt{\left(x-1\right)\left(x+3\right)}=2\)
⇔\(x^2+2x-3=4\)
\(\Leftrightarrow x^2+2x-7=0\)
⇔ \(x=-1+2\sqrt{2}\) (tm)
hoặc \(x=-1-2\sqrt{2}\) (tm)
Vậy...
giải theo cách đặt ẩn giúp mình ạ, mình đang cần gấp
ĐK: \(x\ge-2\)
Đặt \(\left\{{}\begin{matrix}\sqrt{x+2}=a\ge0\\\sqrt{x^2-2x+4}=b\ge0\end{matrix}\right.\Leftrightarrow a^2+b^2=x^2-x+6\), PTTT:
\(5ab=2\left(a^2+b^2\right)\\ \Leftrightarrow2a^2-5ab+2b^2=0\\ \Leftrightarrow\left(a-2b\right)\left(2a-b\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}a=2b\\2a=b\end{matrix}\right.\)
Với \(a=2b\Leftrightarrow x+2=4\left(x^2-2x+4\right)\)
\(\Leftrightarrow4x^2-8x+16=x+2\\ \Leftrightarrow4x^2-9x+14=0\\ \Delta=81-224< 0\\ \Leftrightarrow x\in\varnothing\)
Với \(2a=b\Leftrightarrow4\left(x+2\right)=x^2-2x+4\)
\(\Leftrightarrow4x+8=x^2-2x+4\\ \Leftrightarrow x^2-6x-4=0\\ \Delta=36+16=52\\ \Leftrightarrow\left[{}\begin{matrix}x=3+\sqrt{13}\left(tm\right)\\x=3-\sqrt{13}\left(tm\right)\end{matrix}\right.\)
Vậy PT có nghiệm \(x=3\pm\sqrt{13}\)
Lời giải:
ĐKXĐ: $x\geq -2$
PT $\Leftrightarrow 5\sqrt{(x+2)(x^2-2x+4)}=2(x^2-x+6)$
Đặt $\sqrt{x+2}=a; \sqrt{x^2-2x+4}=b(a,b\geq 0)$ thì pt trở thành:
$5ab=2(a^2+b^2)$
$\Leftrightarrow 2a^2-5ab+2b^2=0$
$\Leftrightarrow (2a-b)(a-2b)=0$
$\Rightarrow 2a=b$ hoặc $a=2b$
Nếu $2a=b\Leftrightarrow 4a^2=b^2$
$\Leftrightarrow 4(x+2)=x^2-2x+4$
$\Leftrightarrow x=3\pm \sqrt{13}$ (tm)
Nếu $a=2b\Leftrightarrow a^2=4b^2$
$\Leftrightarrow x+2=4(x^2-x+6)$
$\Leftrightarrow 4x^2-5x+22=0$ (dễ thấy pt này vô nghiệm)
1/cho x>2014. Chứng minh bất đẳng thức sau:
\(\frac{\sqrt{x-2013}}{x+2}\) + \(\frac{\sqrt{x-2014}}{x}\)\(\le\)\(\frac{1}{2\sqrt{2015}}\)+\(\frac{1}{2\sqrt{2014}}\)(bằng cách đặt ẩn phụ để áp dụng BĐT Cauchy)
2/cho x,y,z>0. chứng minh BĐT sau:
\(\frac{x}{2x+y+z}\)+\(\frac{y}{x+2y+z}\)+\(\frac{z}{x+y+2z}\)\(\le\) 3/4 (bằng cách đặt ẩn phụ để áp dụng BĐT Cauchy)
các bạn giải thật kĩ giúp nha! nếu giải bằng cách đặt ẩn phụ để áp dụng BĐT Cauchy không được thì suy nghĩ cách khác giúp mình nhé. Mình đang cần gấp. Thanhks
1/ Đặt \(\hept{\begin{cases}\sqrt{x-2013}=a\\\sqrt{x-2014}=b\end{cases}}\)
Thì ta có:
\(\frac{\sqrt{x-2013}}{x+2}+\frac{\sqrt{x-2014}}{x}=\frac{a}{a^2+2015}+\frac{b}{b^2+2014}\)
\(\le\frac{a}{2a\sqrt{2015}}+\frac{b}{2b\sqrt{2014}}=\frac{1}{2\sqrt{2015}}+\frac{1}{2\sqrt{2014}}\)
2/ \(\frac{x}{2x+y+z}+\frac{y}{x+2y+z}+\frac{z}{x+y+2z}\)
\(\le\frac{1}{4}\left(\frac{x}{x+y}+\frac{x}{x+z}+\frac{y}{y+x}+\frac{y}{y+z}+\frac{z}{z+x}+\frac{z}{z+y}\right)\)
\(=\frac{3}{4}\)
Giải PT (có đặt ẩn phụ)
a. x^2 +2y^2=4x+4y-6
(giúp mik vs ạ)
=>x^2-4x+2y^2-4y+6=0
=>x^2-4x+4+2y^2-4y+2=0
=>(x-2)^2+2(y-1)^2=0
=>x=2 và y=1
\(\hept{\begin{cases}u+v=\frac{9}{160}\\u=\frac{5}{4}.v\end{cases}}\)
Đặt ẩn phụ giúp mình với.
Phân tích đa thức thành nhân tử:
a. (6x+5)2(3x+2)(x+1)-35
b. (4x-2)(10x+4)(5x+7)(2x+1)+17
Chú ý: giải bằng cách đặt ẩn phụ
CÁC BẠN GIÚP MÌNH VỚI!