tìm u và v biết u+2=4 và u^(2)+v^(2)= 65
Tìm hai số u,v trong mỗi trường hợp sau:
a) u+v = 29 và u.v = 198
b) u+v = \(3\sqrt{2}\) và u.v = 4
c) u-v = -2 và u.v = -80
d) \(u^2+v^2=13\) và u.v = 6
a) Vì u+v=29 và uv=198 nên u,v là hai nghiệm của phương trình:
\(x^2-29x+198=0\)
\(\Leftrightarrow x^2-18x-11x+198=0\)
\(\Leftrightarrow x\left(x-18\right)-11\left(x-18\right)=0\)
\(\Leftrightarrow\left(x-18\right)\left(x-11\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-18=0\\x-11=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=18\\x=11\end{matrix}\right.\)
Vậy: u=18; v=11
Tìm hai số u, v trong mỗi trường hợp sau:
a) u + v = \(3\sqrt{2}\) và u.v =4
b) u - v = -2 và u.v = 80
c) \(u^2+v^2\) = 13 và u.v = 16
a) Vì \(u+v=3\sqrt{2}\) và uv=4
nên u,v là hai nghiệm của phương trình: \(x^2-3\sqrt{2}x+4=0\)
\(\Delta=\left(-3\sqrt{2}\right)^2-4\cdot1\cdot4=18-16=2>0\)
Vì \(\Delta>0\) nên phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{3\sqrt{2}-\sqrt{2}}{2}=\sqrt{2}\\x_2=\dfrac{3\sqrt{2}+\sqrt{2}}{2}=2\sqrt{2}\end{matrix}\right.\)
Vậy: \(u=\sqrt{2};v=2\sqrt{2}\)
a) Giải hệ phương trình: \(\hept{\begin{cases}\frac{3}{\sqrt{x-4}}+\frac{4}{y+2}=7\\\frac{5}{\sqrt{x-4}}-\frac{1}{y+2}=4\end{cases};}\)
b) Tìm hai số u và v thỏa mãn: \(u^2+v^2=65\)và \(uv=-28\)
AI GIẢI NHANH VỚI Ạ!!!!
Câu a em nghĩ có thể làm như vầy ạ,câu b để sau (em mới lớp 7,cần suy ra nghĩ thêm)
a)ĐKXĐ: x > 4; \(y\ne2\)
Đặt \(\frac{1}{\sqrt{x-4}}=a;\frac{1}{y+2}=b\)
Hệ phương trình trở thành: \(\hept{\begin{cases}3a+4b=7\\5a-b=4\end{cases}}\Leftrightarrow\hept{\begin{cases}3a+4b=7\\20a-4b=16\end{cases}}\)
Cộng theo vế với vế của hai phương trình trong hệ,ta được: \(23a=7+16=23\Rightarrow a=1\Rightarrow b=1\)
Đến đây dễ rồi ạ.
b)
\(u^2+v^2+2uv=65-56=9=\left(u+v\right)^2=9\Rightarrow\orbr{\begin{cases}u+v=3\\u+v=-3\end{cases}}\)
\(u^2+v^2-2uv=65+56=121=\left(u-v\right)^2=121\Rightarrow\orbr{\begin{cases}u-v=11\\u-v=-11\end{cases}}\)
tự làm tiếp
Cho vecto u = (m\(^2\) + m - 2; 4) và vecto v = (m ; 2). Tìm m để hai vecto u, v cùng phương
- Với \(m=0\) ko thỏa mãn
- Với \(m\ne0\) hai vecto cùng phương khi:
\(\dfrac{m^2+m-2}{m}=\dfrac{4}{2}\Leftrightarrow m^2+m-2=2m\)
\(\Rightarrow m^2-3m-2=0\Rightarrow m=\dfrac{3\pm\sqrt{17}}{2}\)
b1:tìm 2 số u và v biết u-v=5, uv=24
xét các ước của 24 hợp lý có:
u=8 và v=3
hoặc u=-3 và v=-8
Thấy uv=24 suy ra ta có các cặp sau
u=1 v=24
u=24 v=1
u=2 v=12
u=12 v=2
u=4 v=6
u=6 v=4
u=3 v=8
u=8 v=3..................
mà ta thấy u-v=5 suy ra u=8 v= 3
KẾT LUẬN : Vậy u=8 v=3
Trong không gian với hệ tọa độ Oxyz, biết u → = 2 ; v → = 1 ; và góc giữa hai vectơ u → và v → bằng 2 π 3 . Tìm k để vectơ p → = k u → + v → vuông góc với vectơ q → = u → - v → .
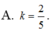
![]()
![]()
![]()
u và v là cá số thực dương thỏa mãn u + v =4
Tìm GTNN của \(P=u^2+v^2+\frac{33}{uv}\)
Mất 1 tiếng sau khi nhìn cái đề mới giải đc
Ta có \({u+v}≥ 2uv\)
\(=>{(u+v)^2-2uv}≥2uv\)
\(<=>{(u+v)^2/ 2}≥ 2uv\)
Và \({(u+v)^2/4}≥uv\)
\(P= {u^2+v^2}+{33 \over uv}\)
\(≥ {2uv}+{33\over uv}\)
\(={(u+v)^2 \over 2}+{33/{(u+v)^2 \over 4}}\)
Thế số vào ta sẽ đc kết quả \({65 \over 4}\)
Vậy GTNN của P là 65/4 khi u=v = 2
Sai!
Ta có \(P=u^2+v^2+\frac{33}{uv}\)
\(\ge\frac{\left(u+v\right)^2}{2}+\frac{33}{\frac{\left(u+v\right)^2}{4}}\)
\(=\frac{4^2}{2}+\frac{33}{\frac{4^2}{4}}=\frac{65}{4}\)
"=" <=> u=v=2
Áp dụng bđt : a^2+b^2 >= (a+b)^2 và ab < = (a+b)^2/4 thì :
P >= (u+v)^2/2 + 33/[(u+v)^2/4]
= 4^2/4 + 33/(4^2/4)
= 49/4
Dấu "=" xảy ra <=> u=v=2
Vậy ..............
Tk mk nha
cho 2 số u và v biết uv = 9 và u + v = 22 khi đó U và v là hai nghiệm của phương trình
4. Nêu cách tìm hai số, biết tổng S và tích P của chúng.
Tìm hai số u và v trong mỗi trường hợp sau:
a ) u + v = 3 u v = − 8 b ) u + v = − 5 u v = 10