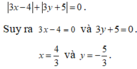|3x-4|+|3y+5|=0

Những câu hỏi liên quan
Tìm x biết :
a) ( 2x - 5 | + | 3y + 1 | = 0
b) | 3x - 4 | + | 3y - 5 | = 0
c) | 2x - 5 | + | xy - 3y + 2 | = 0
\(a\text{) }\left|2x-5\right|+\left|3y+1\right|=0\)
\(\Rightarrow\left\{{}\begin{matrix}\left|2x-5\right|=0\\\left|3y+1\right|=0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}2x-5=0\\3y+1=0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}2x=5\\3y=-1\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{5}{2}\\y=-\dfrac{1}{3}\end{matrix}\right.\)
Vậy \(\left\{{}\begin{matrix}x=\dfrac{5}{2}\\y=-\dfrac{1}{3}\end{matrix}\right.\)
b) \(\left|3x-4\right|+\left|3y-5\right|=0\)
\(\Rightarrow\left\{{}\begin{matrix}\left|3x-4\right|=0\\\left|3y-5\right|=0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}3x-4=0\\3y-5=0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}3x=4\\3y=5\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{4}{3}\\y=\dfrac{5}{3}\end{matrix}\right.\)
Vậy \(\left\{{}\begin{matrix}x=\dfrac{4}{3}\\y=\dfrac{5}{3}\end{matrix}\right.\)
c) \(\left|2x-5\right|+\left|xy-3y+2\right|=0\)
\(\Rightarrow\left\{{}\begin{matrix}\left|2x-5\right|=0\\\left|xy-3y+2\right|=0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}2x-5=0\\xy-3y+2=0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}2x=5\\xy-3y=-2\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{5}{2}\\xy-3y=-2\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{5}{2}\\\dfrac{5}{2}y-3y=-2\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{5}{2}\\\left(\dfrac{5}{2}-3\right)y=-2\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{5}{2}\\\left(-\dfrac{1}{2}\right)y=-2\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{5}{2}\\y=4\end{matrix}\right.\)
Vậy \(\left\{{}\begin{matrix}x=\dfrac{5}{2}\\\left(-\dfrac{1}{2}\right)y=-2\end{matrix}\right.\)
Đúng 0
Bình luận (0)
/3x -4/ +/3y + 5 / =0
\(\left|3x-4\right|+\left|3y+5\right|=0\)
\(\left\{{}\begin{matrix}\left|3x-4\right|\ge0\\\left|3y+5\right|\ge0\end{matrix}\right.\)
\(\Rightarrow\left|3x-4\right|+\left|3y+5\right|\ge0\)
Dấu "=" xảy ra khi:
\(\left\{{}\begin{matrix}\left|3x-4\right|=0\Rightarrow3x=4\Rightarrow x=\dfrac{4}{3}\\\left|3y+5\right|=0\Rightarrow3y=-5\Rightarrow y=\dfrac{-5}{3}\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Cái này là đại số chứ phải hình học đâu?
Đúng 0
Bình luận (2)
chọn và giải ra luôn nhé Trong mặt phẳng Oxy, phương trình đường thẳng d đi qua A(1;-2) và vuông góc với đường thẳng ∆:3x-2y+x=0 là A. 3x-2y-7=0 B.2x+3y+4=0 C.x+3y+5=0 D.2x+3y-3=0
Bài 1 : Tìm x , y biết :
a) | 2x - 5 | + | 3y + 1 | = 0
b) | 3x - 4 | + | 3y - 5 | = 0
c) | 16 - | x | + 5y - 2 | = 0
a.
\(\left[{}\begin{matrix}2x-5=0\\3y+1=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}2x=5\\3y=-1\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=\dfrac{5}{2}\\y=\dfrac{-1}{3}\end{matrix}\right.\)
b.
\(\left[{}\begin{matrix}3x-4=0\\3y-5=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}3x=4\\3y=5\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=\dfrac{4}{3}\\y=\dfrac{5}{3}\end{matrix}\right.\)
chúc bạn học tốt ![]()
Đúng 0
Bình luận (0)
|3x-4|+|3y+5|=0
vì l 3x-4l+l3y+5l = 0
=> \(\hept{\begin{cases}3x-4=0\\3y+5=0\end{cases}}\Rightarrow\hept{\begin{cases}x=\frac{4}{3}\\y=\frac{-5}{3}\end{cases}}\)
Đúng 0
Bình luận (0)
Tìm x, y thoả mãn: 3 x − 4 + 3 y + 5 = 0
tìm x,y:|3x-4|+|3y+5|=0
\(\left|3x-4\right|+\left|3y+5\right|=0\)
\(\Rightarrow\hept{\begin{cases}3x-4=0\\3y+5=0\end{cases}\Rightarrow\hept{\begin{cases}3x=4\\3y=-5\end{cases}\Rightarrow\hept{\begin{cases}x=\frac{4}{3}\\y=-\frac{5}{3}\end{cases}}}}\)
Vậy x=4/3 và y= -5/3
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
đường thẳng đi qua A(1;-2) và vuông góc với đường thẳng d: 3x - y + 1 = 0
A.x+3y+1=0 B.-x-3y+4=0
C.x+3y+3=0 D.x+3y+5=0
tim x:
a. /3x-4/+/3y+5/=0
b./12x+8/+/11y-5/=<0