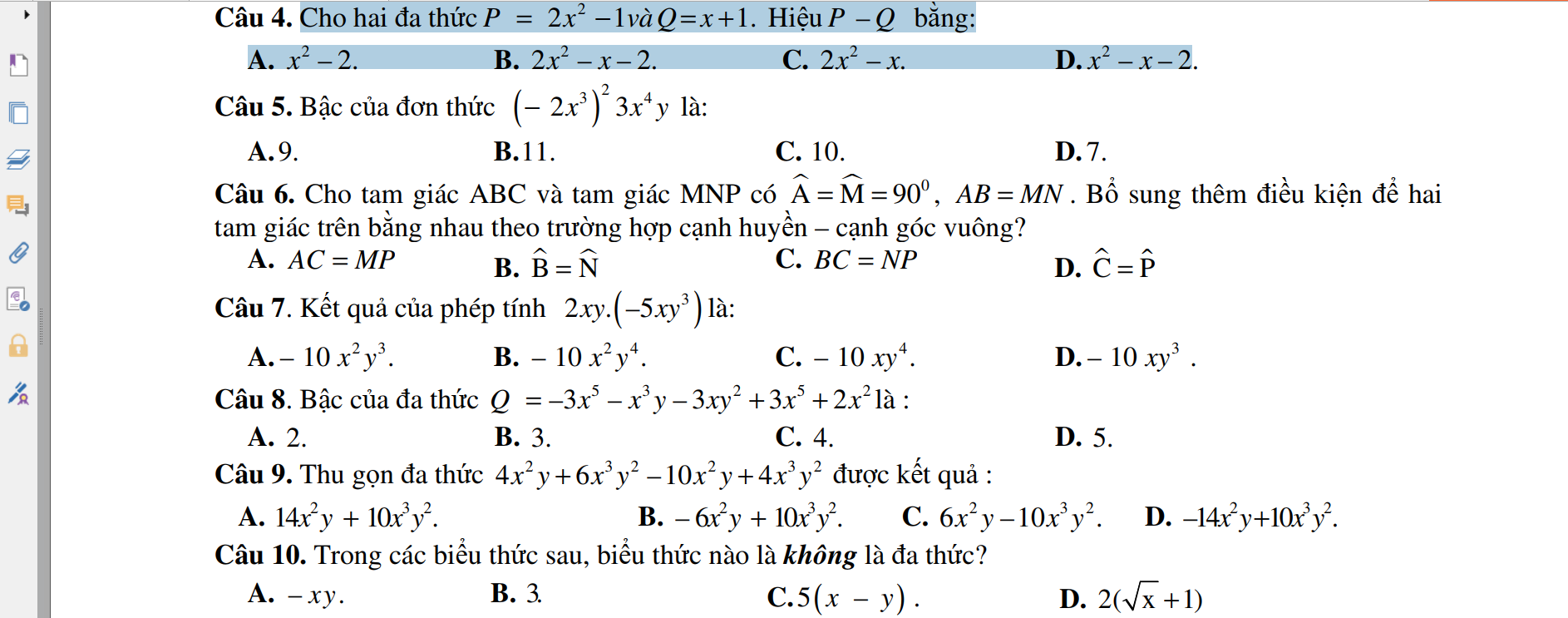
Mình đag cần rất rất gấp.Mong mọi ng giúp
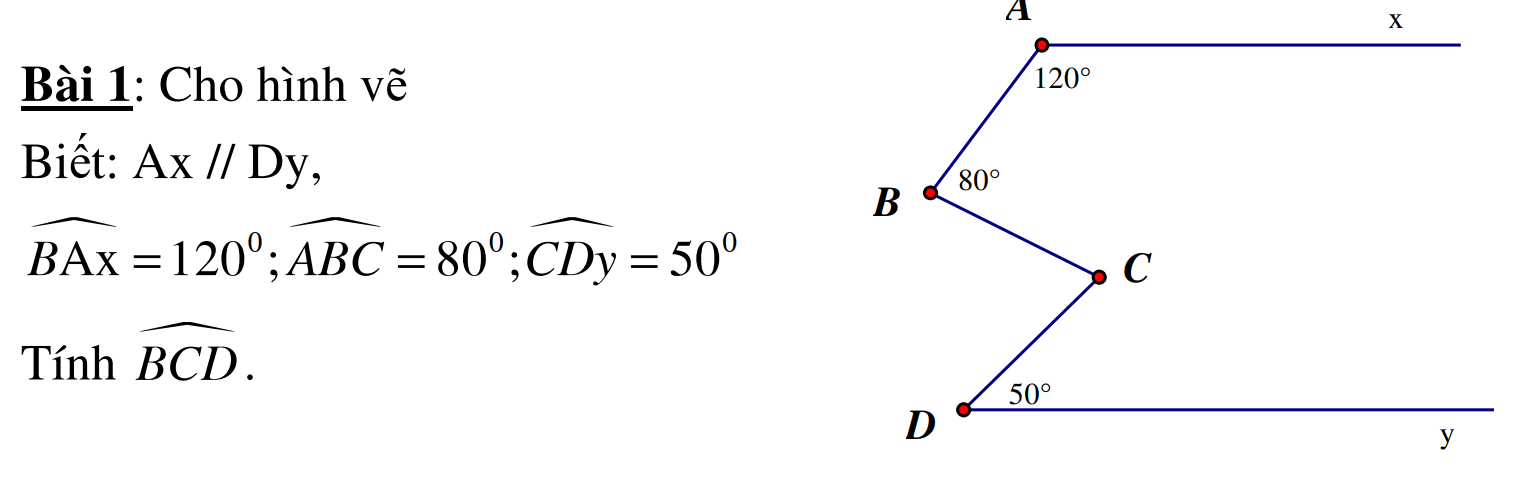
Mình đag cần rất rất gấp. mọi ng giúp mình vớiiiiiiiiiiiiiiiiii
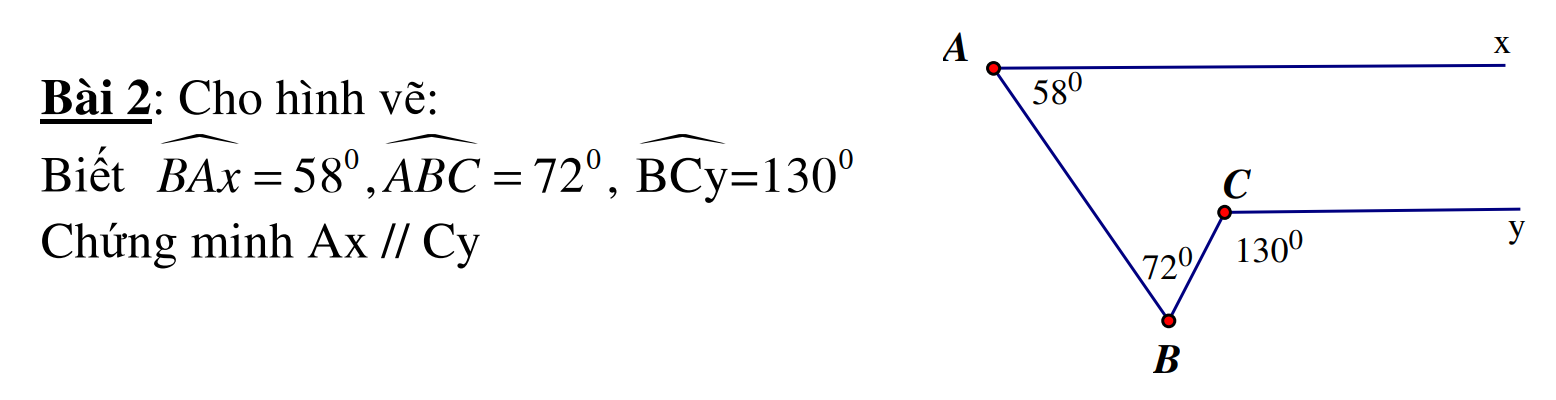
Mình đag cần rất rất gấp. mọi ng giúp mình vớiiiiiiiiiiii
từ điểm B kẻ \(Bz//Cy=>\angle\left(BCy\right)+\angle\left(CBz\right)=180^o\)(góc trong cùng phía)
\(=>\angle\left(CBz\right)=180^o-130^o=50^o\)
\(=>\angle\left(ABz\right)=\angle\left(ABC\right)+\angle\left(CBz\right)=50^o+72^o=122^o\)
\(=>\angle\left(BAx\right)+\angle\left(ABz\right)=180^o\)
mà 2 góc này ở vị trí trong cùng phía
\(=>Ax//Bz=>Ax//Cy\)
Mình đag cần rất rất gấp. mọi ng giúp mình vớiiiiiiiiiiiii
kẻ Bz//Ax=>Bz//Cy
\(=>\angle\left(BAx\right)+\angle\left(ABz\right)=180^o\)(tgosc trong cùng phía)
\(=>\angle\left(ABz\right)=180^o-100^o=80^o\)
\(=>\angle\left(CBz\right)=80+40=120^o=\angle\left(BCy\right)\)(so le trong)
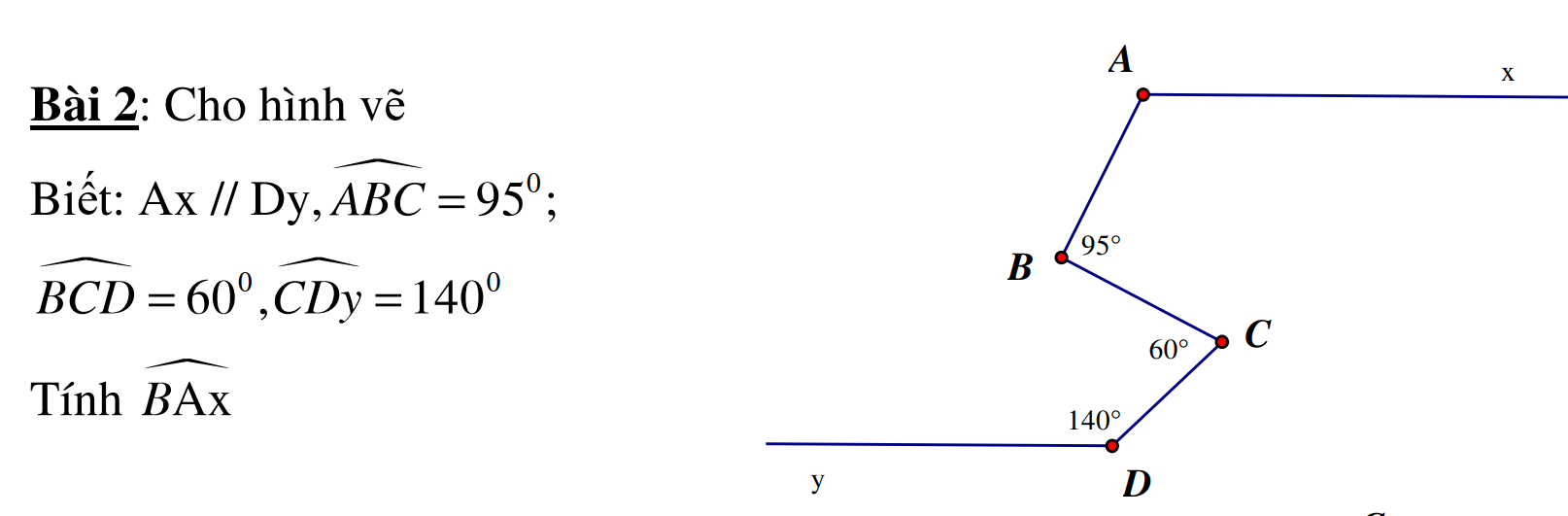
Mình đag cần rất rất gấp. mọi ng giúp mình vớiiiiiiiiiiiii akkkkkkkkkkk
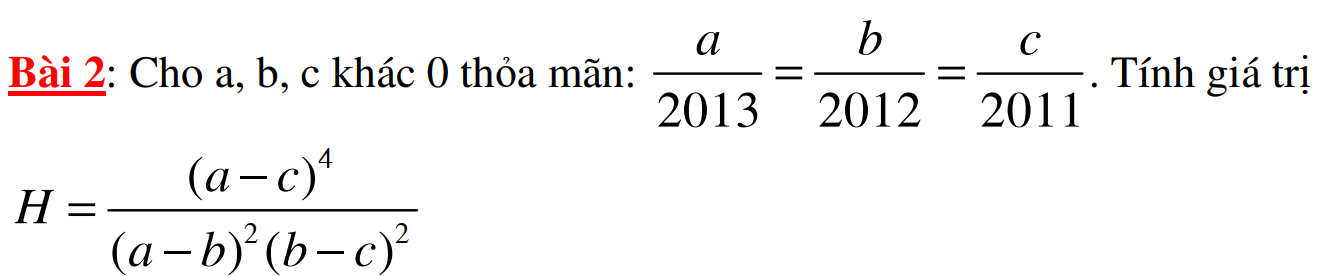
mình đag cần rất rất gấp. Mọi ng giúp mình vớiiiiiiiiiiii ak.
Áp dụng t/c dãy tỉ số bằng nhau
\(\dfrac{a}{2013}=\dfrac{b}{2012}=\dfrac{c}{2011}=\dfrac{a-c}{2}=\dfrac{a-b}{1}=\dfrac{b-c}{1}\\ \Rightarrow a-c=2\left(a-b\right)=2\left(b-c\right)\)
\(\Rightarrow H=\dfrac{\left[2\left(a-b\right)\right]^4}{\left(a-b\right)^2\left(a-b\right)^2}=\dfrac{16\left(a-b\right)^4}{\left(a-b\right)^4}=16\)
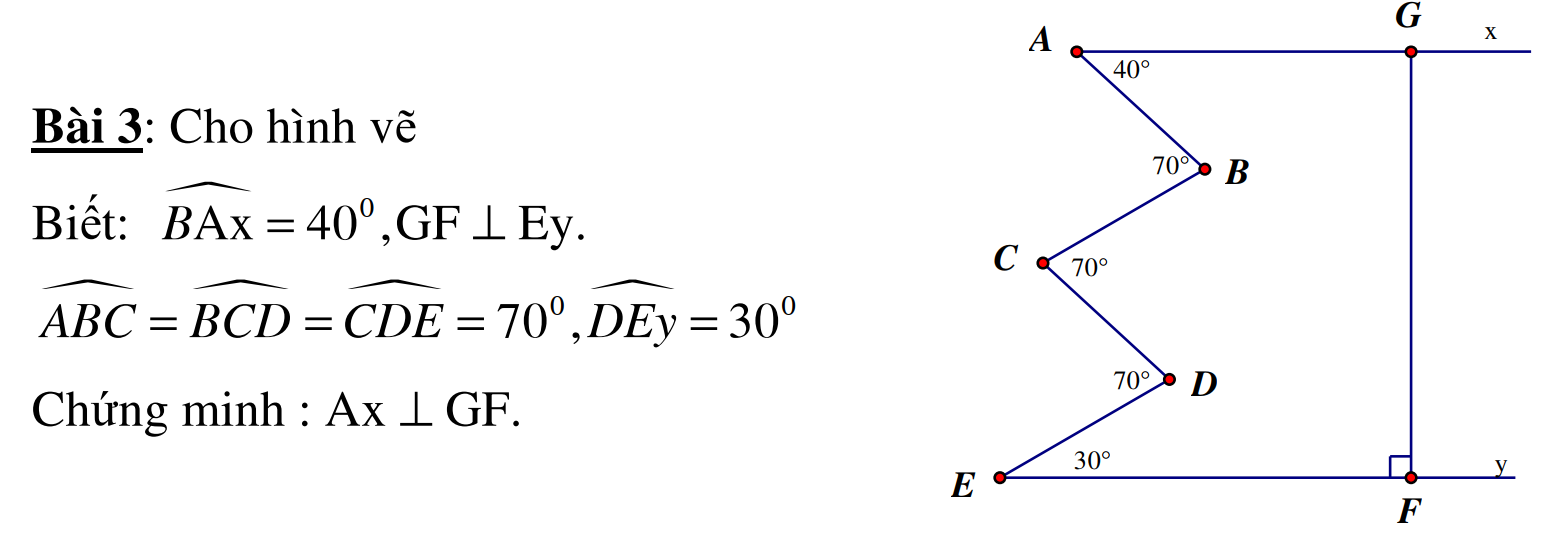
Mình đag cần rất rất gấp. mọi ng giúp mình vớiiiiiiiiiiiii akkkkkkkkkkk
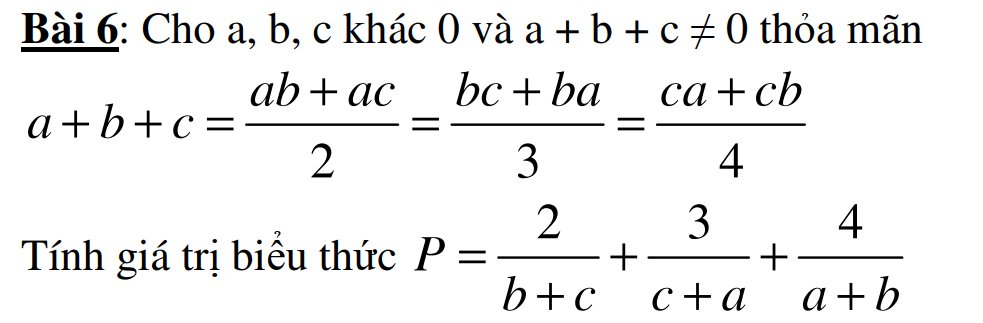
mình đag cần rất rất gấp. Mọi ng giúp mình vớiiiiiiiiiiii ak. mình sẽ tick
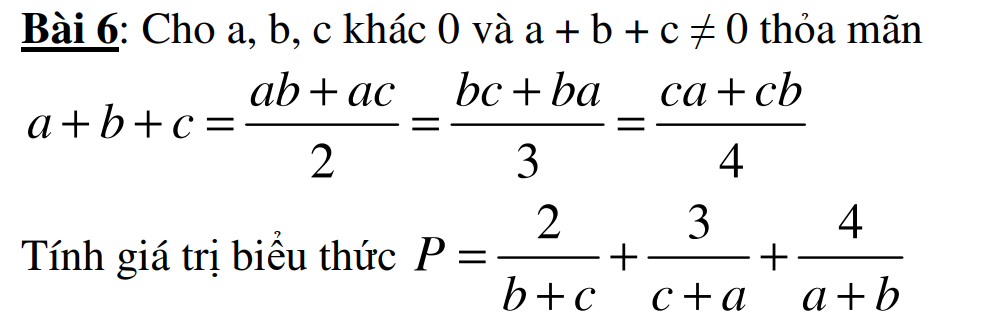
mình đag cần rất rất gấp. Mọi ng giúp mình vớiiiiiiiiiiii ak. mình sẽ tick
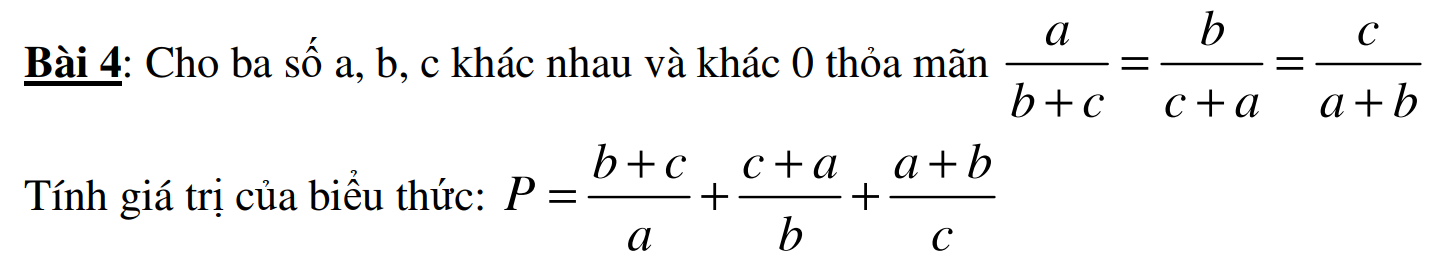
mình đag cần rất rất gấp. Mọi ng giúp mình vớiiiiiiiiiiii ak. mình sẽ tick
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{a}{b+c}=\dfrac{b}{c+a}=\dfrac{c}{a+b}=\dfrac{a+b+c}{2\left(a+b+c\right)}=\dfrac{1}{2}\)
\(\Rightarrow\left\{{}\begin{matrix}b+c=2a\\c+a=2b\\a+b=2c\end{matrix}\right.\)
\(\Rightarrow P=\dfrac{b+c}{a}+\dfrac{c+a}{b}+\dfrac{a+b}{c}=\dfrac{2a}{a}+\dfrac{2b}{b}+\dfrac{2c}{c}=2+2+2=6\)
P=
\(\dfrac{b+c}{a}+\dfrac{c+a}{b}+\dfrac{a+b}{c}=\dfrac{a}{b+c}.\left(\dfrac{b+c}{a}+\dfrac{c+a}{b}+\dfrac{a+b}{c}\right):\left(\dfrac{a}{b+c}\right)=\left(\dfrac{b+c}{a}.\dfrac{a}{b+c}+\dfrac{c+a}{b}.\dfrac{a}{b+c}+\dfrac{a+b}{c}.\dfrac{a}{b+c}\right):\dfrac{a}{b+c}=\left(\dfrac{b+c}{a}.\dfrac{a}{b+c}+\dfrac{c+a}{b}.\dfrac{b}{c+a}+\dfrac{a+b}{c}.\dfrac{c}{a+b}\right):\dfrac{a}{b+c}=\left(1+1+1\right):\dfrac{a}{b+c}=3.\dfrac{b+c}{a}=\dfrac{3b+3c}{a}\)