Đáp án C

Tam giác ABC có góc A là góc tù nên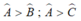 

Mà cạnh đối diện với góc A là cạnh BC .

Áp dụng định lí: trong 1 tam giác cạnh đối diện với góc lớn hơn thì lớn hơn ta được:

BC > AC và BC > AB

Vậy tam giác ABC có độ dài cạnh BC là lớn nhất nên dây BC gần tâm nhất.

Chưa thể kết luận dây nào xa tâm nhất.

a)Xét tứ giác MBOC có 

\(\widehat{OBM}\) và \(\widehat{OCM}\) là hai góc đối

\(\widehat{OBM}+\widehat{OCM}=180^0\left(90^0+90^0=180^0\right)\)

Do đó: MBOC là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)

1)Cho tam giác nhọn ABC (AB<AC) nội tiếp đường tròn (O). Gọi H là trực tâm của tam giác ABC, K là giao điểm thứ hai của AH với đường tròn (O). Đường thẳng đi qua H và vuông góc với OA cắt BC ở I. Chứng minh rằng IK là tiếp tuyến của đường tròn (O)

 ~~~~~~~~~ Bài làm ~~~~~~~~~

Ta có: \(\widehat{HBD}=\widehat{DAC}\) (Cùng phụ với \(\widehat{ACB}\))

\(\widehat{KBD}=\widehat{DAC}\)( Góc nối tiếp cùng chắn cung \(KC\))

\(\Rightarrow\widehat{HBD}=\widehat{KBD}\)

Ta lại có: \(BD\perp HK\)

\(\Rightarrow BD\) là đường trung trực của \(HK\)

\(\Rightarrow\Delta IHK\) cân tại \(I\)

\(\Rightarrow\widehat{BKD}=\widehat{BHD}=\widehat{AHQ}\)

Lại có:\(\widehat{DKO}=\widehat{HAO}\)( \(\Delta OKA\) cân tại \(O\))

Vì vậy: \(\widehat{DKO}+\widehat{BKD}=\widehat{HAO}+\widehat{AHQ}=90^0\)

\(\Rightarrow\widehat{KIO}=90^0\)

\(\Rightarrow IK\)là tiếp tuyến của đường tròn \(\left(O\right)\)

(Hình vẽ chỉ mang tính chất minh họa cái hình vẽ gần cả tiếng đồng hồ :)) )

Ủa bạn ơi sao phụ nhau? Dòng đầu ấy

Đúng rồi bạn. Phụ nhau ý nghĩa là ^HBD + ^ACB = 90^0 và tương tự như góc kia. (Tam giác vuông ý)

a: góc BHD+góc BMD=180 độ

=>BHDM nội tiếp

b: BHDM nội tiếp

=>góc HDM+góc HBM=180 độ

=>góc ADM=góc ABC

=>góc ADM=góc ADC

=>DA là phân giáccủa góc MDC

c: Xét tứ giác DHNC có

góc DHC=góc DNC=90 độ

=>DHNC nội tiếp

=>góc NHD=góc NDC

góc NHD+góc MHD

=180 độ-góc NCD+góc MBD

=180  độ+180 độ-góc ABD-góc ACD

=180 độ

=>M,H,N thẳng hàng

a: góc BEH+góc BFH=90 độ

=>BEHF nội tiếp

b: góc ABK=1/2*sđ cung AK=90 độ

Xét ΔABK vuông tại B và ΔAFC vuông tại F có

góc AKB=góc ACF

=>ΔABK đồng dạng với ΔAFC

opps hihi xin lỗi lúc nảy em làm vội nên sai,thế này mới chính là câu trả lời của em

Lời giải. Kẻ OA₁⊥BC,OB₁⊥AC,OC₁⊥AB. Khi đó tứ giác OA₁C₁B,OA₁B₁C,OC₁AB₁ nội tiếp nên theo định lý Ploteme ta có

     ⎨aR=bz+cy

        az=cx+bR⇒R(a+b+c)=b(z−x)+c(y−x)+a(y+z)(1)

        ay=bx+cR

Ta lại có 2SABC=r(a+b+c)=cz+by−ax (2)

Cộng (1)với (2) ta thu được R+r=y+z−x. ■