Giúp em câu 2 với em cảm ơn :((
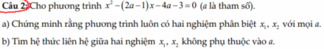
giúp em câu 2 và câu 4 với ạ, em cảm ơn
Giải giúp em câu 1, câu 2, câu 4 với ạ em cảm ơn
2.
Áp dụng định lý hàm cosin:
\(b=\sqrt{a^2+c^2-2ac.cosB}=\sqrt{8^2+3^2-2.8.3.cos60^0}=7\)
\(S_{ABC}=\dfrac{1}{2}ac.sinB=\dfrac{1}{2}.8.3.sin60^0=6\sqrt{3}\)
4.
\(\Delta=\left(m+2\right)^2-16>0\Leftrightarrow m^2+4m-12>0\Rightarrow\left[{}\begin{matrix}m>2\\m< -6\end{matrix}\right.\) (1)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-m-2\\x_1x_2=4\end{matrix}\right.\)
\(x_1+x_2+x_1x_2>1\)
\(\Leftrightarrow-m-2+4>1\)
\(\Rightarrow m< 1\) (2)
Kết hợp (1); (2) ta được \(m< -6\)
Giúp em câu 2 với
Em cảm ơn ạ 
Giúp em câu 2 với
Em cảm ơn ạ

Giúp em câu 2 với ạ em cảm ơn
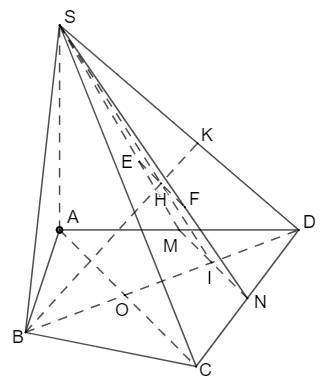
a) Trong (ABCD): Gọi O là giao điểm của AC và BD.
SO là giao tuyến của (SAC) và (SBD).
b) Gọi M là trung điểm của AD, N là trung điểm của CD.
Trong (ABCD) gọi I là giao điểm của BD và MN.
Trong (SMN) gọi H là giao điểm của SI và EF.
Trong (SBD) gọi K là giao điểm của BH và SD.
K là giao của SD với (BEF).
Giúp em câu 2 với
Em cảm ơn nhiều ạ
Giúp em 2 câu này với ạ em cảm ơn!
ĐKXĐ: \(x\le4\)
\(\Leftrightarrow\left(x^3+3x^2+3x+1\right)+6\left(x+1\right)-\left(4-x\right)\sqrt{4-x}-6\sqrt{4-x}=0\)
\(\Leftrightarrow\left(x+1\right)^3+6\left(x+1\right)-\left(\sqrt{4-x}\right)^3-6\sqrt{4-x}=0\)
Đặt \(\left\{{}\begin{matrix}x+1=a\\\sqrt{4-x}=b\ge0\end{matrix}\right.\)
\(\Rightarrow a^3+6a-b^3-6b=0\)
\(\Rightarrow\left(a-b\right)\left(a^2+ab+b^2\right)+6\left(a-b\right)=0\)
\(\Rightarrow\left(a-b\right)\left[\left(a+\dfrac{b}{2}\right)^2+\dfrac{3b^2}{4}+6\right]=0\)
\(\Rightarrow a=b\)
\(\Rightarrow\sqrt{4-x}=x+1\left(x\ge-1\right)\)
\(\Rightarrow4-x=x^2+2x+1\)
\(\Rightarrow x^2+3x-3=0\Rightarrow\left[{}\begin{matrix}x=\dfrac{-3+\sqrt{21}}{2}\\x=\dfrac{-3-\sqrt{21}}{2}< -1\left(loại\right)\end{matrix}\right.\)
 Giúp em câu 2 với ạ. Em cảm ơn nhiều
Giúp em câu 2 với ạ. Em cảm ơn nhiều
Câu 2
a, Thay \(m=-2\) vào \(\left(1\right)\)
\(x^2-2x+\left(-2\right)-1=0\\ \Rightarrow x^2-2x-3=0\\ \Delta=\left(-2\right)^2-4.1.\left(-3\right)=16\\ \Leftrightarrow\left\{{}\begin{matrix}x_1=\dfrac{2+4}{2}=3\\x_2=\dfrac{2-4}{2}=-1\end{matrix}\right.\)
Vậy với m =-1 thì phương trình có hai nghiệm x =3 ; x= -1
2, \(\Delta=\left(-2\right)^2-4.1.\left(m-1\right)=4-4m+4\\ =-4m+8\)
phương trình có hai nghiệm phân biệt \(\Delta>0\\ \Rightarrow-4m+8>0\\ \Leftrightarrow m< 2\)
Áp dụng hệ thức vi ét
\(\left\{{}\begin{matrix}x_1+x_2=2\left(1\right)\\x_1.x_2=m-1\left(2\right)\end{matrix}\right.\)
Kết hợp \(\left(1\right)\) và \(x_1+2x_2=0\) ta có hệ
\(\left\{{}\begin{matrix}x_1+x_2=2\\x_1+2x_2=0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x_1=4\\x_2=-2\end{matrix}\right.\)
Thay \(x_1=4;x_2=-2\) vào 2
\(\Rightarrow4.\left(-2\right)=m-1\\ \Rightarrow m=-7\left(t/m\right)\)
Vậy \(m=-7\)
Câu 1:
\(\left\{{}\begin{matrix}2x+y=5\\3x-y=5\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}5x=10\\3x-y=5\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{10}{5}=2\\3.2-y=5\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=2\\6-y=5\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=6-5\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=1\end{matrix}\right.\)
Mọi người giúp e với giải giúp em câu 2 và câu 3 ạ em xin cảm ơn 