Cho tam giác ABC, có BC = a, góc A = α và hai trung tuyến BM và CN vuông góc với nhau. Tính S.ABC

Những câu hỏi liên quan
Cho tam giác ABC có BC = a, góc BAC = 60 độ và hai đường trung tuyến BM và CN vuông góc với nhau. Tính diện tích tam giác
cho tam giác ABC vuông tại B, BC = 20132014 cm, hai đường trung tuyến BM và CN vuông góc với nhau. Tính CN ?
Dùng hình bạn Ngọc nhé (khỏe khỏi phải vẽ :)
Xét \(\Delta BOC\)và \(\Delta NBC\)có
\(\widehat{OCB}\)chung
\(\widehat{BOC}=\widehat{NBC}=90\)
\(\Rightarrow\Delta BOC\)đồng dạng \(\Delta NBC\)
\(\Rightarrow\frac{BC}{NC}=\frac{OC}{BC}\Leftrightarrow BC^2=NC.OC\)
\(\Leftrightarrow BC^2=NC.\frac{2}{3}NC=\frac{2NC^2}{3}\)(Vì O là trọng tâm)
\(\Rightarrow NC=\sqrt{\frac{3}{2}}BC=\frac{\sqrt{3}.20132014}{\sqrt{2}}\)
Đúng 0
Bình luận (0)
chịu@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho tam giác ABC vuông tại B, cạnh BC = 20132014 cm; hai trung tuyến BM và CN vuông góc với nhau. Tính CN ?
Cho tam giác ABC vuông tại B, cạnh BC = 20132014 cm; hai trung tuyến BM và CN vuông góc với nhau. Tính CN ?
Cho tam giác ABC có hai đường trung tuyến BM,CN vuông góc với nhau và có BC= 4 , góc BAC = 30 độ.Tính diện tích của tam giác ABC.
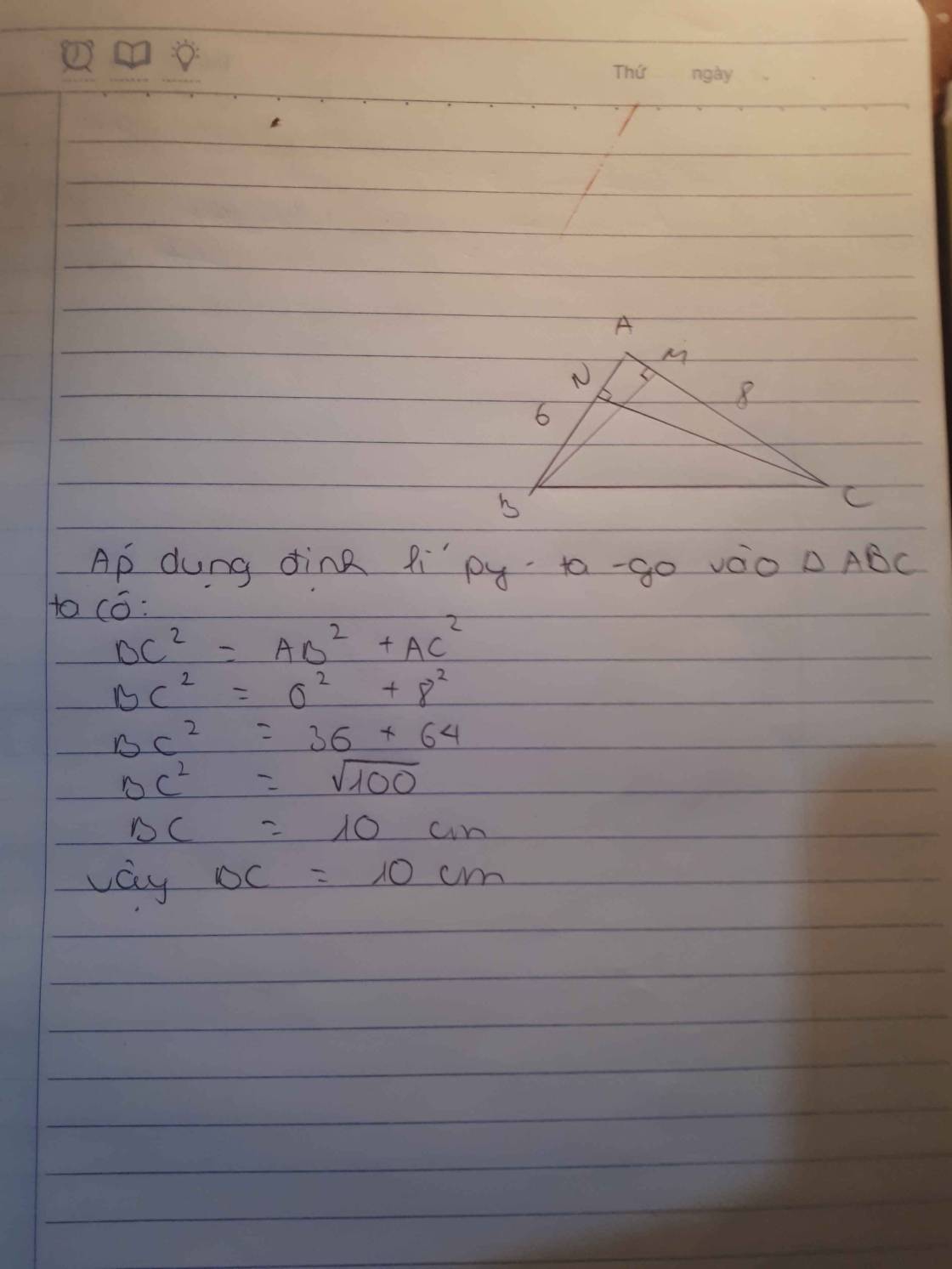
Cho tam giác ABC có AB = 6,AC = 8 và hai đường trung tuyến BM,CN vuông góc với nhau. Tính độ dài cạnh BC
cho tam giac abc vuông tai B canh BC= 20132014 cm ; hai trung tuyến BM và CN vuông góc với nhau .Tính CN?
Cho tam giác ABC vuông tại B, cạnh BC = 18,6 cm; hai trung tuyến BM, Cn vuông góc với nhau. Tính CN
cho tam giác ABC vuông cân tại a , các trung tuyến BM,CN cắt nhau tại O
a, tam giác BCM = tam giác CBN
b, AO vuông góc BC
c, Từ A và N lần lượt kẻ AK , NH vuông góc với BM ( K,H thuộc BM ) Chứng minh tam giác AKH vuông cân và CH = AC
a, tam giác ABC cân tại A (gt)
=> AB = AC (Đn)
có M;N lần lượt là trung điểm của AC;AB (gt) => AM = MC = 1/2AC và AN = BN = 1/2BC (tc)
=> AN = AM = BN = CM
xét tam giác NBC và tam giác MCB có : BC chung
^ABC = ^ACB do tam giác ABC cân tại A (Gt)
=> tam giác NBC = tam giác MCB (c-g-c) (1)
b, (1) => ^KBC = ^KCB (đn)
=> tam giác KBC cân tại K (dh)
c, có tam giác ABC cân tại A (gt) => ^ABC = (180 - ^BAC) : 2 (tc)
có AM = AN (câu a) => tam giác AMN cân tại A (đn) => ^ANM = (180 - ^BAC) : 2 (tc)
=> ^ABC = ^ANM mà 2 góc này đồng vị
=> MN // BC (đl)
Đúng 0
Bình luận (0)