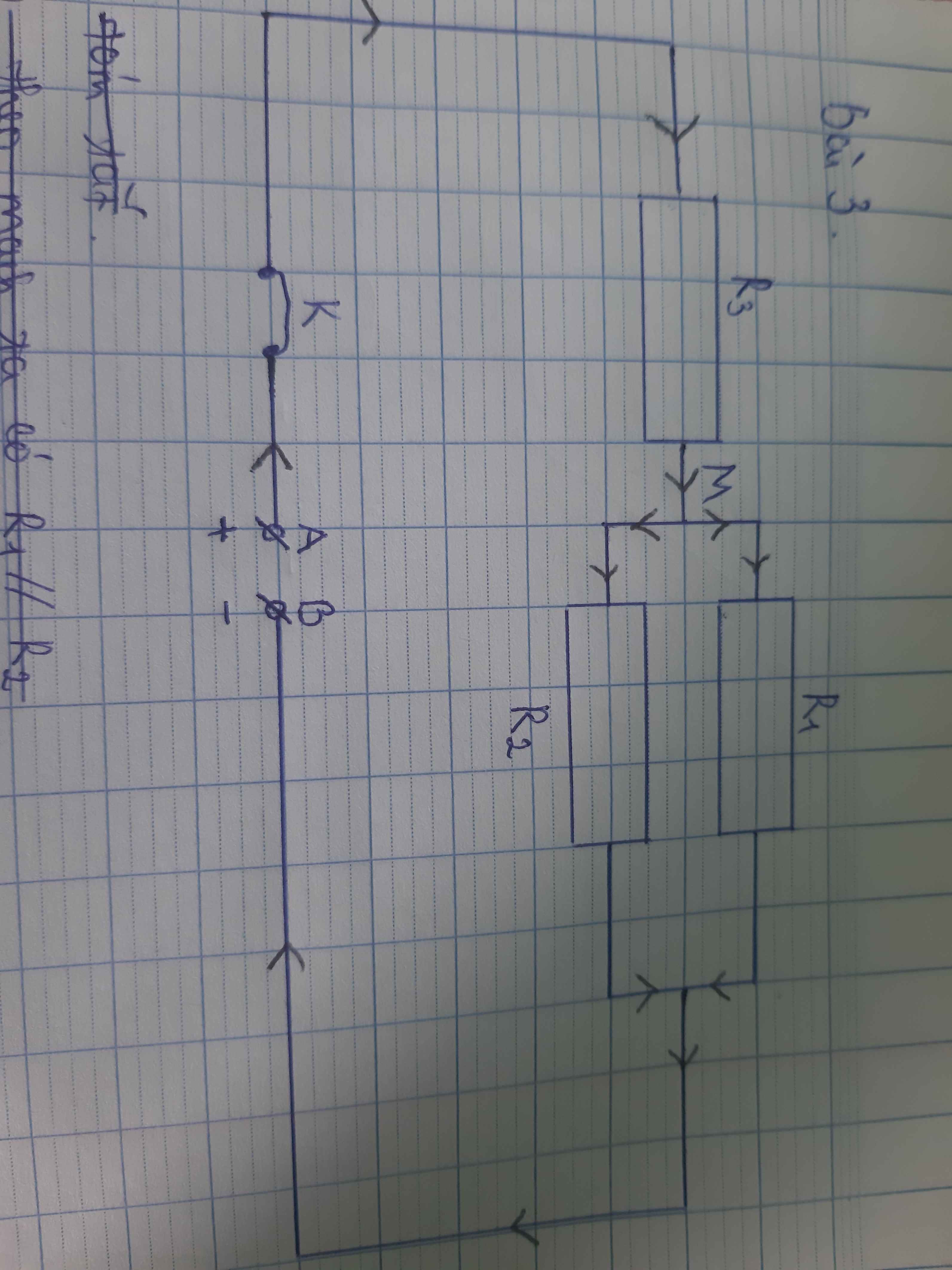
vẽ sơ đồ đoạn thẳng hiệu tỉ vẽ như thế nào ?

Những câu hỏi liên quan
Ai cho mình hỏi vẽ sơ đồ không thẳng như thế nào vậy ?
như thế nào là đoạn mạch nối tiếp , vẽ sơ đồ minh họa , viết các hệ thức định luật ôm cho đoạn mạch nối tiếp
- Các thiết bị điện hay dụng cụ điện được mắc nối tiếp với nhau trong mạch điện được hiểu là đoạn mạch nối tiếp
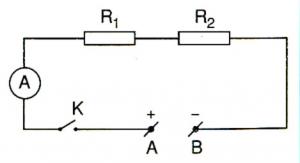
I1 = I2 = ... = In
UAB = U1 + U2 + ... + Un
Rtđ = R1 + R2 +...+ Rn
Đúng 1
Bình luận (0)
Cho đoạn mạch AB có sơ đồ như hình vẽ, bỏ qua điện trở của dây nối. Hiệu điện thế giữa hai điểm A và B có biểu thức là A. UAB E +I(R+r) B. UAB E – I(R+r) C. UAB - E + I(R+r) D. UAB - E – I (R+r)
Đọc tiếp
Cho đoạn mạch AB có sơ đồ như hình vẽ, bỏ qua điện trở của dây nối. Hiệu điện thế giữa hai điểm A và B có biểu thức là
![]()
A. UAB = E +I(R+r)
B. UAB = E – I(R+r)
C. UAB = - E + I(R+r)
D. UAB = - E – I (R+r)
Đáp án: A
HD Giải: Khi đi từ A đến B ta gặp cực dương của nguồn (E > 0), dòng điện cùng chiều từ A->B nên UAB = E +I(R+r)
Đúng 0
Bình luận (0)
2. Cho sơ đồ mạch điện như hình vẽ. Biết hiệu điện thế hai đầu đoạn mạch AB khôngđổi. Hỏi:a) Khi dịch chuyển con chạy C của biến trở tiến dần về phía đầu N thì độ sáng của đènthay đổi như thế nào? Giải thích. b) Khi dịch chuyển con chạy C của biến trở tiến dần về phía đầu M thì độ sáng của đèn thay đổi như thế nào? Giải thích.
Đọc tiếp
2. Cho sơ đồ mạch điện như hình vẽ. Biết hiệu điện thế hai đầu đoạn mạch AB không
đổi. Hỏi:
a) Khi dịch chuyển con chạy C của biến trở tiến dần về phía đầu N thì độ sáng của đèn
thay đổi như thế nào? Giải thích. b) Khi dịch chuyển con chạy C của biến trở tiến dần về phía đầu M thì độ sáng của đèn thay đổi như thế nào? Giải thích.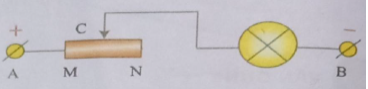
Cho mạch điện có hiệu điện thế 220V, nếu có 2 bóng đèn 110V và 2 bóng 220V thì mắc cúng vào mạch như thế nào? Vẽ sơ đồ nguyên lí của mạch điện trên
cho mạch điện có sơ đồ như hình vẽ r1 = 10 ôm r2 = 20 ôm hiệu điện thế giữa hai đầu đoạn mạch ab bằng 12v. a) vẽ chiều dòng điện trong mạch, tính điện trở tương đương của đoạn mạch . b) tính số chỉ của vôn kế và ampe kế
cho sơ đồ mạch điện như hình vẽ biết r2 = 6 ôm , vôn kế chỉ 1,2 vôn, ampe kế chỉ 1,2A . Tính hiệu điện thế giữa 2 đầu đoạn mạch AB và điện trở R1
Vẽ sơ đồ trong câu hỏi như thế nào
Hãy tìm các đoạn thẳng tỉ lệ trong hình vẽ sơ đồ một góc công viên ở Hình 4.

Ta có:
\(AD = 1,5m;AE = 3m;BD = 3m;EC = 6m;\)
\(AB = AD + DB = 1,5 + 3 = 4,5m;AC = AE + EC = 3 + 6 = 9m\)
Ta có:
\(\frac{{AD}}{{BD}} = \frac{{1,5}}{3} = \frac{1}{2};\frac{{AE}}{{EC}} = \frac{3}{6} = \frac{1}{2}\). Do đó, \(AD\) và \(BD\) tỉ lệ với \(AE\) và \(EC\).
\(\frac{{AD}}{{AB}} = \frac{{1,5}}{{4,5}} = \frac{1}{3};\frac{{AE}}{{AC}} = \frac{3}{9} = \frac{1}{3}\). Do đó, \(AD\) và \(AB\) tỉ lệ với \(AE\) và \(AC\).
\(\frac{{AB}}{{BD}} = \frac{{4,5}}{3} = \frac{3}{2};\frac{{AC}}{{EC}} = \frac{9}{6} = \frac{3}{2}\). Do đó, \(AB\) và \(BD\) tỉ lệ với \(AC\) và \(EC\).
Đúng 1
Bình luận (0)