Với điều kiện: \(x>0;x\ne4;x\ne1\): Cho \(P=\sqrt{x}-1\). Tìm m để có x thoả mãn \(P=mx\sqrt{x}-2mx+1\)

Những câu hỏi liên quan
Điều kiện của m để bpt: (2m+1)x+ m-5 ≥ 0 nghiệm đúng với mọi x: 0 < x < 1
A. -1/2 < m < 5
B. m = 5
C. m = 5 và m = -1/2
D. m ≥ 5
Chọn D
Bpt đã cho tương đương với ( 2m+1) x ≥ 5-m (*)
TH1: Với m> -1/2, bpt (*) trở thành: 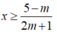
Tập nghiệm của bpt là 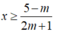
Để bpt đã cho nghiệm đúng với mọi x:
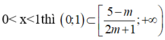
Hay 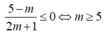
TH2: nếu m= -1/2 , bpt (*) trở thành: 0x ≥ 5+1/2
Bpt vô nghiệm => không có m thòa mãn
TH3: Với m< -1/2, bpt (*) trở thành: 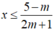
Tập nghiệm của bpt là 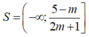
Để bpt đã cho nghiệm đúng với 0< x< 1 thì
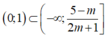
Hay 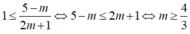
Kết hợp điều kiện m< -1/2 nên không có m thỏa mãn
Vậy với m≥ 5, bất phương trình đã cho nghiệm đúng với mọi x: 0< x< 1
Đúng 0
Bình luận (0)
Tìm điều kiện của a để:
3
-
5
2
x
-
2
a
+
1
3
+
5
2
-
2
a
≤
0...
Đọc tiếp
Tìm điều kiện của a để:
3 - 5 2 x - 2 a + 1 3 + 5 2 - 2 a ≤ 0
với ∀ x ≥ 0
A. a ≤ 0
B. 0 ≤ a ≤ 1
C. a ≥ 1
D. a ≥ 0
cho x thuộc Z , A = (1-x)4 . -x với điều kiện nào của x thì A = 0 , A>0, A<0
Điều kiện của m để bất phương trình ( 2m+1) x+ m-5 ≥ 0 nghiệm đúng với mọi x thỏa mãn 0< x< 1 :
A. -1/2 < m < 5
B. m = 5
C. m= 5 và m= 1
D. m ≥ 5
Chọn D
Ta có: ( 2m+1) x+ m-5 ≥ 0 tương đương: ( 2m+ 1) x≥ 5- m (*)
+ TH1: Với m> -1/2 , bất phương trình (*) trở thành: 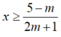
Tập nghiệm của bất phương trình là 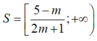
Để bất phương trình đã cho nghiệm đúng với 0< x< 1 thì 
Hay 
+ TH2: m= -1/ 2, bất phương trình (*) trở thành: 0x ≥ 5+ 1/2
Bất phương trình vô nghiệm. Nên không có m thỏa mãn
+ TH3: Với m< -1/ 2 , bất phương trình (*) trở thành: 
Tập nghiệm của bất phương trình là 
Để bất phương trình đã cho nghiệm đúng với 0< x < 1thì 
Hay 
Kết hợp điều kiện m< -1/ 2 nên không có m thỏa mãn.
Vậy với m ≥ 5, bất phương trình đã cho nghiệm đúng với mọi x: 0< x< 1
Đúng 0
Bình luận (0)
Cho tam thức f(x) = (m-2)x mx m-3=0 a) tìm điều kiện m để pt f(x) =0 vô nghiệm b) tìm điều kiện m để f(x)
Với giá trị nào của tham số m hệ phương trình có nghiệm thỏa mãn điều kiện x > 0, y < 0?
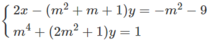
Chú ý rằng m 2 + m + 1 > 0 ; - m 2 - 9 < 0 , ∀m nên nếu x > 0, y < 0 thì phương trình thứ nhất có vế trái dương, vế phải âm. Do đó không có giá trị nào của m làm cho hệ đã cho có nghiệm thỏa mãn điều kiện x > 0, y < 0.
Đúng 0
Bình luận (0)
tính giá trị của biểu thức
A=x-y/x+y biết x,y khác 0 và thỏa mạn điều kiện (x-y)(x-2y)=0
B=x/y biết x,y khác 0 và thỏa mạn điều kiện x+y/x-y=3/2
C=x/y biết x,y khác 0 và thỏa mãn điều kiện x+2y/x-y=3/5
Điều kiện của m để bất phương trình ( m - 3) x+ 3m-7 ≤ 0 nghiệm đúng với ∀ x ∈ (2 ; + ∞) ? A. không có giá trị thỏa mãn B. m 3 C. m 3 D.
m
≤
13
5
Đọc tiếp
Điều kiện của m để bất phương trình ( m - 3) x+ 3m-7 ≤ 0 nghiệm đúng với ∀ x ∈ (2 ; + ∞) ?
A. không có giá trị thỏa mãn
B. m > 3
C. m < 3
D. m ≤ 13 5
Điều kiện xác định của phương trình: x/2x+1 + x+1/3+x = 0
Giúp với ;-;
ĐKXĐ : \(\hept{\begin{cases}2x+1\ne0\\3+x\ne0\end{cases}}\Leftrightarrow\hept{\begin{cases}x\ne-\frac{1}{2}\\x\ne-3\end{cases}}\)
Đáp án:
\(x\ne-\frac{1}{2}\)\(;x\ne3\)
HT
Trả lời:
\(ĐKXĐ:\hept{\begin{cases}2x+1\ne0\Leftrightarrow x\ne-\frac{1}{2}\\3+x\ne0\Leftrightarrow x\ne-3\end{cases}}\)
Xem thêm câu trả lời
Cho tam thức f(x) = (m-2)x +mx+m-3=0
a) Tìm điều kiện m để pt f(x) = 0 vô nghiệm
b) Tìm điều kiện m để f(x)
f(x) = (2m-2)x+m-3=0
Nếu 2m-2=0 => m=1 => f(x)= 0+1-3=0 (vô lí)
=> m=1 (nhận)
Nếu 2m-2\(\ne\)0 => m\(\ne\) 1
f(x) có no x= 3-m/2m-2
=> m\(\ne\)1 (loại)
Vậy m=1 thì f(x) vô nghiệm
Đúng 1
Bình luận (0)
















