a) Xác định hệ số a của paradol y = a\(x^2\), biết rằng paradol đi qua A(-2;-2)
b) Tìm tọa độ của M thuộc paradol nói trên, biết rằng khoảng cách từ M đến trục hoành gấp đôi khoảng cách từ M đến trục tung.
a) Biết đồ thị hàm số y = ax + 7 đi qua M(2; 11). Xác định hệ số a?
b) Biết rằng khi x = 3 thì hàm số y = 2x + b có giá trị bằng 8. Xác định hệ số b?
TÌm tọa độ giao điểm của paradol(P): y = x2 và đường thẳng (d): y = 2x + 3
Phương trình hoành độ giao điểm giữa (P) và (d)
\(x^2=2x+3\)
\(\Leftrightarrow x^2-2x-3=0\)
\(\Delta=\left(-2\right)^2-4.1.\left(-3\right)=16>0\)
\(\Rightarrow x_1=\frac{-b-\sqrt{\Delta}}{2a}=\frac{2-\sqrt{16}}{2.1}=-1\)
\(x_2=\frac{-b+\sqrt{\Delta}}{2a}=\frac{2+\sqrt{16}}{2.1}=3\)
Với x1 =-1 \(\Rightarrow\) y1 = (-1)2 =1 \(\Rightarrow\) A(-1;1)
x2 =3 \(\Rightarrow\)y2 =32 =9 \(\Rightarrow\)B(3;9)
Vậy tọa độ giao điểm là A(-1;1) và B(3;9)
Xác định hệ số a của hàm y = a x 2 , biết rằng đồ thị của nó đi qua điểm A(-2; 1).Vẽ đồ thị của hàm số đó.
Đồ thị hàm số đi qua A(-2; 1)
⇒
1
=
a
.
(
-
2
)
2
⇒ 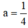
Vậy hàm số: 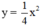
| x | -4 | -2 | 0 | 2 | 4 |
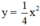 |
4 | 1 | 0 | 1 | 4 |
Đồ thị hàm số:
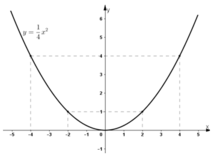
Xác định hệ số a của hàm y = a x 2 , biết rằng đồ thị của nó đi qua điểm A(-2; 1).Vẽ đồ thị của hàm số đó.
Đồ thị hàm số đi qua A(-2; 1)
⇒
1
=
a
.
(
-
2
)
2
⇒ 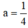
Vậy hàm số: 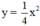
| x | -4 | -2 | 0 | 2 | 4 |
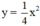 |
4 | 1 | 0 | 1 | 4 |
Đồ thị hàm số:
Cho hàm số bậc nhất y = ax + 3
Xác định hệ số góc a, biết rằng đồ thị của hàm số đi qua điểm A(2; 6).
Hàm số y = ax + 3 là hàm số bậc nhất nên a ≠ 0
Đồ thị của hàm số đi qua điểm A(2; 6) nên:
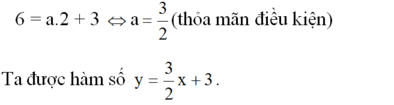
Cho hàm số bậc nhất y = ax + 3
a) Xác định hệ số góc a, biết rằng đồ thị của hàm số đi qua điểm A(2; 6).
b) Vẽ đồ thị của hàm số.
Hàm số y = ax + 3 là hàm số bậc nhất nên a ≠ 0
a) Đồ thị của hàm số đi qua điểm A(2; 6) nên:
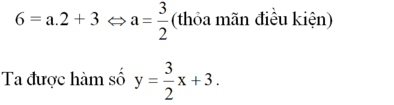
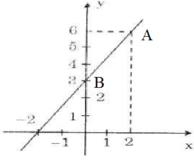
b) Vẽ đồ thị:
- Cho x = 0 thì y = 3 ta được B(0; 3).
Nối A, B ta được đồ thị hàm số
Bài 12: a)Xác định hệ số a của hàm số y = ax2, biết rằng đồ thị hàm số đi qua điểm A(2;-1)
b) Vẽ đồ thị của hàm số đó
CÓ AI CÒN THỨC KO VẬYY
Lời giải:
a) Vì ĐTHS đi qua điểm $A$ nên:
$y_A=ax_A^2$
$\Leftrightarrow -1=a.2^2\Rightarrow a=-\frac{1}{4}$
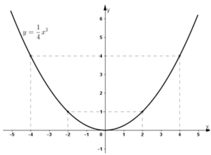
b) Vậy hàm số có công thức: $y=\frac{-1}{4}x^2$
Hình vẽ:
Câu 12. (2 điểm) Cho hàm số y = ax bình phương b) Vẽ đồ thị hàm số với giá trị của a vừa tìm được a) Xác định hệ số a, biết rằng đồ thị hàm số đi qua điểm A(3; 2)
Thay x=3 và y=2 vào y=ax2, ta được:
9a=2
hay a=2/9
Cho hàm số y = (-2a+3)x. Hãy xác định hệ số a biết:
a) Đồ thị của hàm số đi qua điểm A (-1; 4);
b) Đồ thị của hàm số đi qua điểm B (-2; 0);
dễ mà tự giải đi bạn ưi tui ko bít cách giải đâu nên đừn hỏi
ulatroi bn học lớp 7 hả