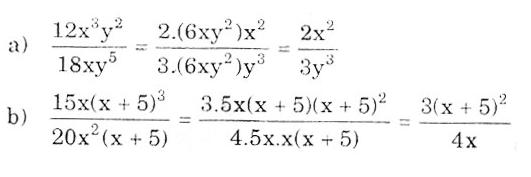Rút gọn phân thức \(\dfrac{20x(2-x)}{12x(x-2)^2}\)

Những câu hỏi liên quan
Rút gọn phân thức :
a) \(\dfrac{12x^3y^2}{18xy^5}\)
b) \(\dfrac{15x\left(x+5\right)^3}{20x^2\left(x+5\right)}\)
a)\(\dfrac{12x^3y^2}{18xy^5}\)=\(\dfrac{2x^2}{3y^3}\)
b)\(\dfrac{15x.\left(x+5\right)^2}{20x^2.\left(x+5\right)}\)=\(\dfrac{3.5x\left(x+5\right)}{4x.5x.\left(x+5\right)}\)=\(\dfrac{3\left(x+5\right)}{4x}\)
Đúng 0
Bình luận (0)
Câu 2 Rút gọn các phân thức sau::(2 điểm )
a/ \(\dfrac{21x^2y^3}{24x^3y^2}\) b/ \(\dfrac{15xy^3\left(x^2-y^2\right)}{20x^2y\left(x+y\right)^2}\)
\(a,\dfrac{21x^2y^3}{24x^3y^2}=\dfrac{7y}{8x}\)
\(b,\dfrac{15xy^3\left(x^2-y^2\right)}{20x^2y\left(x+y\right)^2}=\dfrac{15xy^3\left(x-y\right)\left(x+y\right)}{20x^2y\left(x+y\right)^2}=\dfrac{3y^2\left(x-y\right)}{4x\left(x+y\right)}=\dfrac{3xy^2-3y^3}{4x^2+4xy}\)
Đúng 0
Bình luận (0)
a) Ta có: \(\dfrac{21x^2y^3}{24x^3y^2}\)
\(=\dfrac{21x^2y^3:3x^2y^2}{24x^3y^2:3x^2y^2}\)
\(=\dfrac{7y}{8x}\)
Đúng 0
Bình luận (0)
rút gọn biểu thức B = \(\dfrac{\text{20x - 11}}{\text{x - 2012}}.\dfrac{\text{x(x - 2)}}{\text{1982x}^{\text{2}}+30}-\dfrac{20x-11}{1982x^2+30}:\dfrac{x-2012}{x\left(x-3\right)+2012}\)
\(B=\dfrac{\left(x^2-2x\right)\left(20x-11\right)}{\left(x-2012\right)\left(1982x^2+30\right)}-\dfrac{\left(20x-11\right)\left(x^2-3x+2012\right)}{\left(1982x^2+30\right)\left(x-2012\right)}\left(x\ne2012\right)\\ B=\dfrac{\left(20x-11\right)\left(x^2-2x-x^2+3x-2012\right)}{\left(x-2012\right)\left(1982x^2+30\right)} \\ B=\dfrac{\left(20x-11\right)\left(x-2012\right)}{\left(x-2012\right)\left(1982x^2+30\right)}=\dfrac{20x-11}{1982x^2+30}\)
Đúng 2
Bình luận (0)
Rút gọn phân thức
\(\dfrac{12x^2y\left(x-y\right)}{16xy^2\left(x-y\right)^2}\) có kết quả là
\(\dfrac{12x^2y\left(x-y\right)}{16xy^2\left(x-y\right)^2}\)
\(=\dfrac{3x}{4y\left(x-y\right)}\)
Đúng 1
Bình luận (0)
Rút gọn các phân thức:
a)\(\dfrac{14xy^5\left(2x-3y\right)}{21x^2y\left(2x-3y\right)^2}\) b)\(\dfrac{8xy\left(3x-1\right)^3}{12x^3\left(1-3x\right)}\)
c) \(\dfrac{20x^2-45
}{\left(2x+3\right)^2}\) d) \(\dfrac{5x^2-10xy}{2\left(2y-x\right)^3}\)
\(a,=\dfrac{2y^4}{3x\left(2x-3y\right)}\\ b,=-\dfrac{2y\left(3x-1\right)^2}{3x^2}\\ c,=\dfrac{5\left(4x^2-9\right)}{\left(2x+3\right)^2}=\dfrac{5\left(2x-3\right)\left(2x+3\right)}{\left(2x+3\right)^2}=\dfrac{5\left(2x-3\right)}{2x+3}\\ d,=\dfrac{5x\left(x-2y\right)}{-2\left(x-2y\right)^3}=-\dfrac{5x}{2\left(x-2y\right)^2}\)
Đúng 6
Bình luận (0)
Rút gọn biểu thức A = \(\sqrt{\dfrac{\left(x^2-3\right)^2+12x^2}{x^2}}+\sqrt{\left(x+2\right)^2-8x}\)
đk: x khác 0
A = \(\sqrt{\dfrac{x^4-6x^2+9+12x^2}{x^2}}+\sqrt{x^2+4x+4-8x}\)
= \(\sqrt{\dfrac{x^4+6x^2+9}{x^2}}+\sqrt{x^2-4x+4}\)
= \(\sqrt{\dfrac{\left(x^2+3\right)^2}{x^2}}+\sqrt{\left(x-2\right)^2}\)
= \(\dfrac{x^2+3}{\left|x\right|}+\left|x-2\right|\)
TH1: x \(\ge2\)
A = \(\dfrac{x^2+3}{x}+x-2\)
= \(\dfrac{x^2+3+x^2-2x}{x}=\dfrac{2x^2-2x+3}{x}\)
TH2: \(0< x< 2\)
A = \(\dfrac{x^2+3}{x}-x+2\)
= \(\dfrac{x^2+3-x^2+2x}{x}=\dfrac{2x+3}{x}\)
TH3: x < 0
A = \(\dfrac{x^2+3}{-x}-x+2\)
= \(\dfrac{-x^2-3}{x}-x+2=\dfrac{-x^2-3-x^2+2x}{x}=\dfrac{-2x^2+2x-3}{x}\)
Đúng 2
Bình luận (0)
Rút gọn phân thức:
\(a,\dfrac{2x^3-7x^2-12x+45}{3x^3-19x^2+33x-9}\)
\(b,\dfrac{x^3+x^2-4x-4}{x^3+8x^2+17x+10}\)
\(a)\frac{2x^3-7x^2-12x+45}{3x^3-19x^2+33x-9}=\frac{(x-3)^2(2x+5)}{(3x-1)(x-3)^2}(ĐK:x\ne3,x\ne\frac{1}{3})\)
\(=\frac{2x+5}{3x-1}\)
Còn bài b bạn tự làm nhé
Đúng 0
Bình luận (0)
Điều kiện: \(x\ne\left\{-1;-2;-5\right\}\)
\(\frac{x^3+x^2-4x-4}{x^3+8x^2+17x+10}=\frac{x^2\left(x+1\right)-4\left(x+1\right)}{x^2\left(x+1\right)+7x\left(x+1\right)+10\left(x+1\right)}\)
\(=\frac{\left(x+1\right)\left(x^2-4\right)}{\left(x+1\right)\left(x^2+7x+10\right)}\)
\(=\frac{\left(x+1\right)\left(x-2\right)\left(x+2\right)}{\left(x+1\right)\left[x\left(x+2\right)+5\left(x+2\right)\right]}\)
\(=\frac{\left(x+1\right)\left(x-2\right)\left(x+2\right)}{\left(x+1\right)\left(x+2\right)\left(x+5\right)}=\frac{x-2}{x+5}\)
Điều kiện: \(x\ne\left\{3;\frac{1}{3}\right\}\)
\(\frac{2x^3-7x^2-12x+45}{3x^3-19x^2+33x-9}=\frac{2x^3-6x^2-x^2+3x-15x+45}{3x^3-9x^2-10x^2+30x+3x-9}\)
\(=\frac{2x^2\left(x-3\right)-x\left(x-3\right)-15\left(x-3\right)}{3x^2\left(x-3\right)-10x\left(x-3\right)+3\left(x-3\right)}\)
\(=\frac{\left(x-3\right)\left(2x^2-x-15\right)}{\left(x-3\right)\left(3x^2-10x+3\right)}\)
\(=\frac{2x^2-x-15}{3x^2-10x+3}=\frac{2x\left(x-3\right)+5\left(x-3\right)}{3x\left(x-3\right)-\left(x-3\right)}\)
\(=\frac{\left(2x+5\right)\left(x-3\right)}{\left(3x-1\right)\left(x-3\right)}=\frac{2x+5}{3x-1}\)
Đúng 0
Bình luận (0)
Rút gọn phân thức sau: a) (3x-6)/(x^3-6x^2+12x-8) b) (x^3+2x^2)/(x^3+6x^2+12x+8)
a: \(=\dfrac{3\left(x-2\right)}{\left(x-2\right)^3}=\dfrac{3}{\left(x-2\right)^2}\)
b: \(=\dfrac{x^2\left(x+2\right)}{\left(x+2\right)^3}=\dfrac{x^2}{\left(x+2\right)^2}\)
Đúng 2
Bình luận (1)
1. Rút gọn phân thức \(\dfrac{\left(x+y\right)^2}{x^2-y^2}=\) ta được kết quả là:
2. Rút gọn phân thức \(\dfrac{x^2-3x}{x^2-9}=\)
giúp mình với nhé mình đang cần gấp ạ
1. = \(\dfrac{x+y}{x-y}\)
2. = \(\dfrac{x}{x+3}\)
Đúng 0
Bình luận (0)