Ta có x, y thỏa mãn đẳng thức sau . Khi đó x+y bằng
Những câu hỏi liên quan
Xét khối tứ diện SABC có cạnh SA, BC thỏa mãn:
S
A
2
+
S
B
2
18
và các cạnh còn lại đều bằng 5. Biết thể tích khối tứ diện SABC đạt giá trị lớn nhất có dạng:
V
m
a
x
x
y
4
;
x...
Đọc tiếp
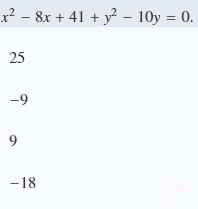
Xét khối tứ diện SABC có cạnh SA, BC thỏa mãn: S A 2 + S B 2 = 18 và các cạnh còn lại đều bằng 5. Biết thể tích khối tứ diện SABC đạt giá trị lớn nhất có dạng: V m a x = x y 4 ; x , y ∈ ℕ * ; (x,y)=1. Khi đó: x, y thỏa mãn bất đẳng thức nào dưới đây?
Xét khối tứ diện SABC có cạnh SA, BC thỏa mãn:
S
A
2
+
B
C
2
18
và các cạnh còn lại đều bằng 5. Biết thể tích khối tứ diện SABC đạt giá trị lớn nhất có dạng:
V
m
a
x
x
y
4
;
x...
Đọc tiếp
Xét khối tứ diện SABC có cạnh SA, BC thỏa mãn: S A 2 + B C 2 = 18 và các cạnh còn lại đều bằng 5. Biết thể tích khối tứ diện SABC đạt giá trị lớn nhất có dạng: V m a x = x y 4 ; x , y ∈ ℕ * ; x , y = 1. Khi đó: x, y thỏa mãn bất đẳng thức nào dưới đây?
A. x + y 2 − x y > 4550.
B. x y + 2 x y > 2550.
C. x 2 − x y + y 2 < 5240.
D. x 3 − y > 19602.
Cho x,y,z là các số thực dương thỏa mãn đẳng thức x^2 + y^2 + z^2 + 2xyz = 1. Khi đó giá trị lớn nhất của biểu thức 2x + y + z bằng bao nhiêu?
Cho x, y, z thỏa mãn x/5=y/8=z/14 và x + 3y − 2z = 5. Khi đó đẳng thức nào dưới đây là sai? (kèm lời giải thích)
A. x = y − 15 B. x + y + 5 = z C. x + y = z D. y + 30 = z
có hay không 2 số tự nhiên x và y có tổng bằng 2003 thỏa mãn đẳng thức :
x^2004 + y^2005 = 2006^2007
Cho x,y là hai số thỏa mãn 2(x2+y2)=(x-y)2. Khi đó ta có hệ thức biểu diễn mối quan hệ giữa x,y là x=....y
2(x2+y2)=(x-y)2 => 2x2+2y2=x2-2xy+y2
x2+y2=-2xy
x2+y2+2xy=0
=>(x+y)2=0 =>x+y=0 => x=-y
Đúng 0
Bình luận (0)
cho x≥0,y≥0 thỏa mãn x+y=1
tìm GTLN, GTNN của P=x/(y+1) + y/(x+1) bằng cách sử dụng bất đẳng thức
Có hay không só x,y thỏa mãn đẳng thức sau
x2+xy+y2-3x-3y+3=0
Cho x và y thỏa mãn đẳng thức: \(\frac{1+3y}{12}=\frac{1+5y}{5x}=\frac{1+7y}{4x}\) khi đó \(x+y=......\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\frac{1+3y}{12}=\frac{1+5y}{5x}=\frac{1+7y}{4x}=\frac{2+10y}{12+4x}=\frac{2.\left(1+5y\right)}{2.\left(6+2x\right)}=\frac{1+5y}{6+2x}\)
=>5x=6+2x
=>3x=6
=>x=2
*x=2 => \(\frac{1+3y}{12}=\frac{1+5y}{10}\Rightarrow10+30y=12+60y\Rightarrow30y=-2\Rightarrow y=-\frac{1}{15}\)
=>x+y=29/15
Đúng 0
Bình luận (0)
cho x+y+z thỏa mãn đẳng thức 4x^2 + 9y^2 + 16z^2 - 4x - 6y - 8z + 3 = 0
khi đó xy+yz+zx=