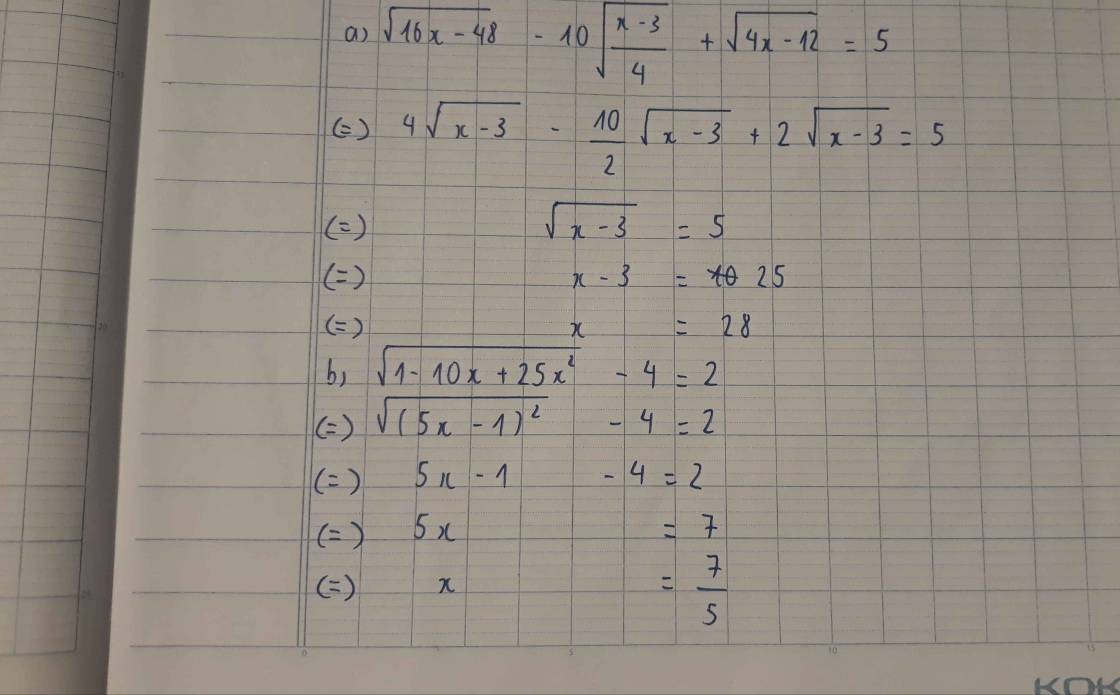a.\(A=\dfrac{x^2-4x+4}{x^3-2x^2-\left(4x-8\right)}=\dfrac{\left(x-2\right)^2}{x^2\left(x-2\right)-4\left(x-2\right)}=\dfrac{\left(x-2\right)^2}{\left(x^2-4\right)\left(x-2\right)}=\dfrac{x-2}{\left(x-2\right)\left(x+2\right)}=\dfrac{1}{x+2}\)

\(A=\dfrac{\left(x-2\right)^2}{x^2\left(x-2\right)-4\left(x-2\right)}\left(x\ne\pm2\right)\\ A=\dfrac{\left(x-2\right)^2}{\left(x-2\right)^2\left(x+2\right)}=\dfrac{1}{x+2}\\ B=\dfrac{x+2-x+\sqrt{x}-1}{\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}\cdot\dfrac{4\sqrt{x}}{3}\left(x>0\right)\\ B=\dfrac{4\sqrt{x}\left(\sqrt{x}+1\right)}{3\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}=\dfrac{4\sqrt{x}}{3\left(x-\sqrt{x}+1\right)}\)

\(\frac{1\text{x}2+2\text{x}4+3\text{x}6+4\text{x}8}{2\text{x}3+4\text{x}6+6\text{x}9+8\text{x}12}\)

\(=\frac{1\text{x}2+2\text{x}4+3\text{x}6+4\text{x}8}{\text{1x}2\text{x}3+2\text{x}4\text{x}3+3\text{x}6\text{x}3+4\text{x}8\text{x}3}\)

\(=\frac{1\text{x}2+2\text{x}4+3\text{x}6+4\text{x}8}{3\left(1\text{x}2+2\text{x}4+3\text{x}6+4\text{x}8\right)}\)

\(=\frac{1}{3}\)

Ta có: \(\frac{1.2+2.4+3.6+4.8}{2.3+4.6+6.9+8.12}=\frac{1.2}{2.3}+\frac{2.4}{4.6}+\frac{3.6}{6.9}+\frac{4.8}{8.12}.\)

                                                       \(=\frac{1}{3}+\frac{1}{3}+\frac{1}{3}+\frac{1}{3}=\frac{1}{3}.4=\frac{4}{3}\)

1x2 + 2x4 + 3x6 + 4x8

= (1x2) (1 + 2 + 3 + 4) 2x3 + 4x6 + 6x9 + 8x12

= (2x3) (1 + 2 + 3 + 4)

Do đó, (1x2 + 2x4 + 3x6 + 4x8 ) / (2x3 + 4x6 + 6x9 + 8x12)

= (1x2) / (2x3) = 1/3

a: Đặt \(x^2-4=a\)

Pt sẽ là \(a=3\sqrt{xa}\)

\(\Rightarrow a^2=9xa\)

\(\Leftrightarrow a\left(a-9x\right)=0\)

\(\Leftrightarrow\left(x^2-4\right)\left(x^2-4-9x\right)=0\)

hay \(x\in\left\{2;-2;\dfrac{9+\sqrt{97}}{2};\dfrac{9-\sqrt{97}}{2}\right\}\)

d: Đặt \(\sqrt{x^2-x+1}=a;\sqrt{x^2+x+1}=b\)

Pt sẽ là 2a+b=ab+2

=>(b-2)(1-a)=0

=>b=2 và 1-a

\(\Leftrightarrow\left\{{}\begin{matrix}x^2+x+1=4\\x^2-x+1=1\end{matrix}\right.\Leftrightarrow x\in\varnothing\)

\(x=1\)

\(P=\dfrac{x^4+5x^3-20x^2-27x+30}{x^2+4x-21}\left(1\right)\)

Điều kiện xác định khi và chỉ khi

\(x^2+4x-21\ne0\)

\(\Leftrightarrow x^2+7x-3x-21\ne0\)

\(\Leftrightarrow x\left(x+7\right)-3\left(x+7\right)\ne0\)

\(\Leftrightarrow\left(x-3\right)\left(x+7\right)\ne0\)

\(\Leftrightarrow\left\{{}\begin{matrix}x\ne3\\x\ne-7\end{matrix}\right.\)

Theo đề bài : \(\)

\(x=\sqrt[]{31-12\sqrt[]{3}}=\sqrt[]{27-12\sqrt[]{3}+4}=\sqrt[]{\left(3\sqrt[]{3}-2\right)^2}=\left|3\sqrt[]{3}-2\right|=3\sqrt[]{3}-2\)

\(\left(1\right)\Leftrightarrow P=\dfrac{x^4-3x^3+8x^3-24x^2+4x^2-12x-15x+45-15}{\left(x-3\right)\left(x+7\right)}\)

\(\Leftrightarrow P=\dfrac{x^3\left(x-3\right)+8x^2\left(x-3\right)+4x\left(x-3\right)-15\left(x-3\right)-15}{\left(x-3\right)\left(x+7\right)}\)

\(\Leftrightarrow P=\dfrac{\left(x-3\right)\left(x^3+8x^2+4x-15\right)-15}{\left(x-3\right)\left(x+7\right)}\)

\(\Leftrightarrow P=\dfrac{x^3+8x^2+4x-15}{x+7}-\dfrac{15}{\left(x-3\right)\left(x+7\right)}\)

\(\Leftrightarrow P=\dfrac{x^3+7x^2+x^2+7x-3x-15}{x+7}-\dfrac{15}{\left(x-3\right)\left(x+7\right)}\)

\(\Leftrightarrow P=\dfrac{x^2\left(x+7\right)+x\left(x+7\right)-3\left(x+7\right)+6}{x+7}-\dfrac{15}{\left(x-3\right)\left(x+7\right)}\)

\(\Leftrightarrow P=\dfrac{\left(x^2+x-3\right)\left(x+7\right)+6}{x+7}-\dfrac{15}{\left(x-3\right)\left(x+7\right)}\)

\(\Leftrightarrow P=x^2+x-3+\dfrac{6}{x+7}-\dfrac{15}{\left(x-3\right)\left(x+7\right)}\)

Thay \(x=3\sqrt[]{3}-2\) vào \(P\) ta được

\(\Leftrightarrow P=\left(3\sqrt[]{3}-2\right)^2+3\sqrt[]{3}-2-3+\dfrac{6}{3\sqrt[]{3}-2+7}-\dfrac{15}{\left(3\sqrt[]{3}-2-3\right)\left(3\sqrt[]{3}-2+7\right)}\)

\(\Leftrightarrow P=31-12\sqrt[]{3}+3\sqrt[]{3}-5+\dfrac{6}{3\sqrt[]{3}+5}-\dfrac{15}{\left(3\sqrt[]{3}-5\right)\left(3\sqrt[]{3}+5\right)}\)

\(\Leftrightarrow P=26-9\sqrt[]{3}+\dfrac{6\left(3\sqrt[]{3}-5\right)}{\left(3\sqrt[]{3}+5\right)\left(3\sqrt[]{3}-5\right)}-\dfrac{15}{\left(3\sqrt[]{3}\right)^2-5^2}\)

\(\Leftrightarrow P=26-9\sqrt[]{3}+\dfrac{6\left(3\sqrt[]{3}-5\right)}{2}-\dfrac{15}{2}\)

\(\Leftrightarrow P=\dfrac{37}{2}-9\sqrt[]{3}+3\left(3\sqrt[]{3}-5\right)\)

\(\Leftrightarrow P=\dfrac{37}{2}-9\sqrt[]{3}+9\sqrt[]{3}-15\)

\(\Leftrightarrow P=\dfrac{37}{2}-15=\dfrac{7}{2}\)

P = 7/2

mình cần gấp mong các bạn giải giùm

c: \(E=\dfrac{\left(x-5\right)^2}{x\left(x-5\right)}=\dfrac{x-5}{x}\)

\(=\left[\left(\dfrac{-\left(x-y\right)}{x-2y}-\dfrac{x^2+y^2+y-2}{\left(x-2y\right)\left(x+y\right)}\right):\dfrac{\left(2x^2+y\right)^2-4}{x\left(x+y\right)+\left(x+y\right)}\right]:\dfrac{x+1}{2x^2+y+2}\)

\(=\dfrac{-x^2+y^2-x^2-y^2-y+2}{\left(x-2y\right)\left(x+y\right)}\cdot\dfrac{\left(x+y\right)\left(x+1\right)}{\left(2x^2+y-2\right)\left(2x^2+y+2\right)}\cdot\dfrac{2x^2+y+2}{x+1}\)

\(=\dfrac{-2x^2-y+2}{\left(x-2y\right)}\cdot\dfrac{\left(x+1\right)}{\left(2x^2+y-2\right)\left(2x^2+y+2\right)}\cdot\dfrac{2x^2+y+2}{x+1}\)

\(=\dfrac{-1}{x-2y}\)

Thay $x=-1,76$ và $y=\dfrac{3}{25}$ vào $P=\dfrac{-1}{x-2y}$, ta được:

$P=\dfrac{-1}{-1,76-2.(\dfrac{3}{25})}=\dfrac{1}{2}$.

\(\dfrac{x-2}{x+1}-\dfrac{3}{x+2}>0.\left(x\ne-1;-2\right).\\ \Leftrightarrow\dfrac{x^2-4-3x-3}{\left(x+1\right)\left(x+2\right)}>0.\\ \Leftrightarrow\dfrac{x^2-3x-7}{\left(x+1\right)\left(x+2\right)}>0.\)    

Đặt \(f\left(x\right)=\dfrac{x^2-3x-7}{\left(x+1\right)\left(x+2\right)}>0.\)

Ta có: \(x^2-3x-7=0.\Rightarrow\left[{}\begin{matrix}x=\dfrac{3+\sqrt{37}}{2}.\\x=\dfrac{3-\sqrt{37}}{2}.\end{matrix}\right.\)

          \(x+1=0.\Leftrightarrow x=-1.\\ x+2=0.\Leftrightarrow x=-2.\)

Bảng xét dấu:

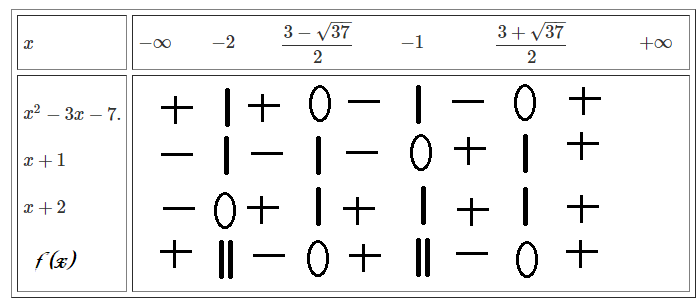
\(\Rightarrow f\left(x\right)>0\Leftrightarrow x\in\left(-\infty-2\right)\cup\left(\dfrac{3-\sqrt{37}}{2};-1\right)\cup\left(\dfrac{3+\sqrt{37}}{2};+\infty\right).\)

\(\sqrt{x^2-3x+2}\ge3.\\ \Leftrightarrow x^2-3x+2\ge9.\\ \Leftrightarrow x^2-3x-7\ge0.\)

\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{3-\sqrt{37}}{2}.\\x=\dfrac{3+\sqrt{37}}{2}.\end{matrix}\right.\)

Đặt \(f\left(x\right)=x^2-3x-7.\)

\(f\left(x\right)=x^2-3x-7.\)

\(\Rightarrow f\left(x\right)\ge0\Leftrightarrow x\in(-\infty;\dfrac{3-\sqrt{37}}{2}]\cup[\dfrac{3+\sqrt{37}}{2};+\infty).\)

\(\Rightarrow\sqrt{x^2-3x+2}\ge3\Leftrightarrow x\in(-\infty;\dfrac{3-\sqrt{37}}{2}]\cup[\dfrac{3+\sqrt{37}}{2};+\infty).\)